How many solutions?
What is the solution to the systems of equations?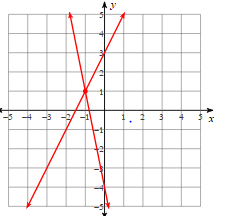
(-1,1)
Solve the systems of equations using substitution:
-3x+4y=-2
y=-5
(-6,-5)
Solve the systems of equations using elimination:
14x+2y=26
-14x-6y=-50
(1,6)
What is the difference between solutions for systems of linear equations and systems of linear inequalities?
Systems of linear equations have one solution (unless no solution or infinite solutions). Systems of inequalities have many solutions.
Ms. Skweres bought 2 new shirts and a dress for $45. She then went back and bought another shirt and 4 dresses for $70.
Write a systems of equations for the situation.
2x+y=45
x+4y=70
What method should you use for the following systems of equations?
3x-5y=10
7y-3x=25
Elimination
What is the solution to the systems of equations?
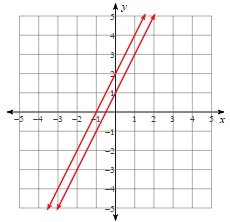
No Solutions
Solve the systems of equations using substitution:
-5x-5y=10
y=-4x-17
(-5,3)
Solve the systems of equations using elimination:
2x+y=7
x-2y=6
(4,-1)
When do you use a dotted line and when do you use a solid line when graphing inequalities?
Dotted: > or <
Solid: > or <
Ms. Blasi went to Dunkin and bought one coffee and a bagel, her total was $7. Ms. Redmond-Mattucci went to Dunkin and bought 2 coffees and 3 bagels for her and her friends and spent $18.
How much does one bagel cost?
One bagel costs $4
Which method would you use to solve the system of equations? Explain your reasoning.
y=4x-5
5+2x=y
Substitution, both equations already have y by itself so you just need to set the two equations equal to each other.
Using your graphing calculator or Desmos, find the solution to the systems of equations:
y=6x-11
-2x-3y=-7
(2,1)
Solve the systems of equations using substitution:
-8x-5y =-24
-x+y=10
(-2,8)
Solve the systems of equations using elimination:
-3x-24y=-66
3x+4y=-14
(-10,4)
You need at least 3 pounds of fruit to make muffins. Blueberries cost $4 per pound, raspberries cost $3 per pound, and you have only $21. If b represents blueberries (in pounds) and r represents raspberries (in pounds), write a systems of equations that represents this scenario.
b+r≥3
4b+3r≤21
Mr. Perez tells his class that the next test is worth 100 points and contains 28 problems. Multiple-choice questions are worth 3 points each and word problems are worth 4 points each. How many of each type of questions are in there?
Let x be the number of multiple choice questions and y be the number of word problems.
(12,16)
There are 12 multiple-choice questions and 16 word problems.
How many solutions does the following system of equations have?
-7x - 5y = -8
8x - 3y = -17
(-1,3)
One Solution, different slopes
Using your graphing calculator or Desmos, find the solution to the systems of equations:
5x+3y=15
10x+6y=20
No Solution
Solve the systems of equations using substitution:
x+3y=1
-3x-3y=-15
(7,-2)
Solve the systems of equations using elimination:
2x+8y=6
-5x-20y=-15
Infinite Number of Solutions
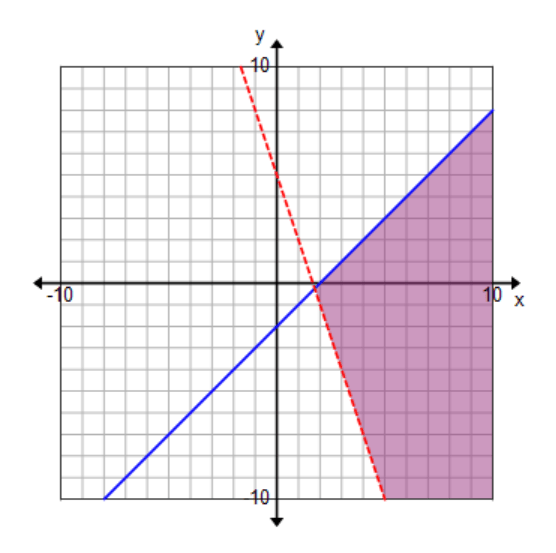
Solve the system of equations by graphing:
y ≤ x − 2
y > −3x + 5
Adult tickets for the school musical sold for $3.50 and student tickets sold for $2.50. On Saturday night, there were 321 total tickets sold for $937.50. How many adult tickets were sold? How many student tickets were sold?
Let x be the number of adult tickets sold and y be the number of student tickets sold.
(135, 186)
There were a total of 135 adult tickets sold and 186 student tickets sold.
How many solutions does the following system of equations have?
3x - y = 19
-3x + y = 10
No Solutions
Using your graphing calculator or Desmos, find the solution to the systems of equations:
2x+8y=6
-5x-20y=-15
Infinite number of solutions
Solve the systems of equations using substitution:
-2x+6y=6
-7x+8y=-5
(3,2)
Solve the systems of equations using elimination:
3+2x-y=0
-3-7y=10x
(-1,1)
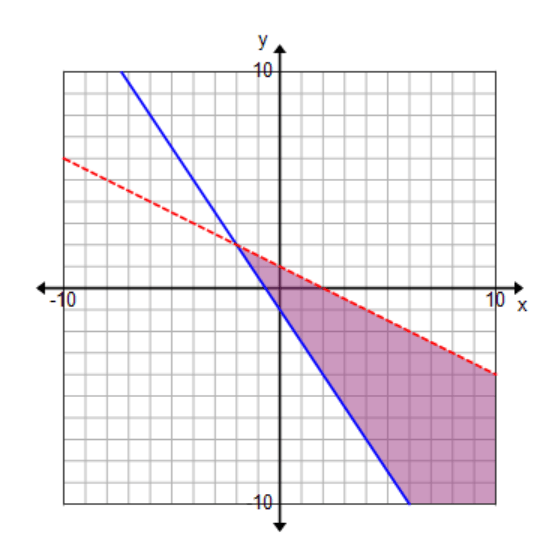
Solve the systems of equations by graphing:
3x+2y≥-2
x+2y<2
Daniella broke her piggy bank open and found that it only contained quarters and pennies. She counted 120 coins with a grand total of $16.32.
How many pennies did Daniella have in her piggy bank?
Daniella had 57 pennies in her piggy bank.
How many solutions does the following system of equations have?
3y+4x=6
12y+16x=24
These are the same exact line (same slope and same y-int), therefore they have Infinite Solutions.