Vocabulary
Transformations
Factor P.S. Binomials
Graphs of Parabolas
Random Topics
100
The name of the graph of a quadratic function.
Parabola
100
The function f(x) = (x - 6)2 + 1 would shift the parabola...
6 spaces to the right and 1 space up
100
Factor the quadratic
x2 - 16
(x+4)(x-4)
100
The vertex of the graph.
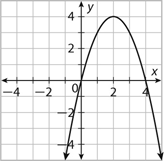
(2,4)
100
Is the "a" value for this function positive or negative?
Negative
200
What is this form of a quadratic equation called?
y=ax2+bx+c
Standard Form
200
Describe how the function
y = 2(x + 3)2 - 8 would differ from y = x2
It would be narrower, shift 3 spaces left and shift 8 spaces down
200
Factor the quadratic
x2 - 25
(x + 5)(x - 5)
200
The roots of the quadratic function are
x=0 and x=4
200
What is the name of the invisible vertical line that goes through the middle of the parabola?
The Axis of Symmetry
300
The lowest or highest point on the parabola.
Vertex
300
Describe how the function
y = -1/2(x - 7)2 would differ from y = x2
It would reflect over the x-axis (be concave down), be wider, and shift 7 spaces to the right.
300
Factor the quadratic
49a2 - 81
(7a + 9)(7a - 9)
300
What is the axis of symmetry?
x = 2
300
Multiply the binomials
(x + 3)(x + 2)
x2 + 5x + 6
400
The name for the points where a parabola crosses the x-axis.
Zeros, Roots or Solutions
400
What is the vertex for the function
y = (x + 9)2 + 2 ?
(-9,2)
400
Factor the quadratic
144x4 - 1
(12x2 + 1)(12x2 - 1)
400
Describe this graph's transformation.
The graph is reflected down, translated 2 spaces right and translated 4 spaces up
400
What is the y-intercept of this parabola?
y=3x2+5
(0,5)
500
Which direction does the "k" value tell the parabola to translate?
y=a(x-h)2+k
Up or Down
500
Write the function for y=g(x) if it shifts the function y=x2
4 units down, 2 units to the left and reflects it over the x-axis.
g(x) = -(x + 2)2 - 4
500
Factor the quadratic
y4 - x2
(y2 + x)(y2 - x)
500
Write the equation of the parabola in vertex form based on the transformation
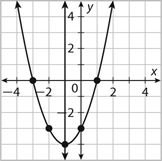
y = (x + 1)2 - 4
500
When studying gravity, which letter in standard form represents the height of the launch platform?
c