Key Parts of the Parabola
Solving Quadratics with ZPP
Graphing
Graphing
Writing Quadratic Equations
100
What is the maximum or minimum point of the parabola called?
Vertex
100
Solve:
y = (x-6)(x+5)
x = 6 and x = -5
100
Graph the following function:
y = (x-4)(x+2)
The parabola should have:
Roots at (4, 0) and (-2, 0)
and a vertex at (1, -9)
100
Graph the following function:
y = x2 +2x -8
The parabola should have:
Roots at (-4, 0) and (2, 0)
and a vertex at (-1, -9)
100
What the equation of the parabola:
With roots at (3, 0) and (5, 0)
and a y-intercept of (0, 15)
y= (x-3)(x-5)
200
What is the graph of a quadratic function called?
Parabola
200
Solve:
y = -2x(x-3)
x = 0
x = 3
200
Graph the following function:
y = 2(x + 3)(x - 3)
The parabola should have:
Roots at (-3, 0) and (3, 0)
and a vertex at (0, -18)
200
Graph the following function:
y = x2 -5x + 6
The parabola should have:
Roots at (2, 0) and (3, 0)
and a vertex at (2.5, -0.25)
200
What the equation for the parabola?
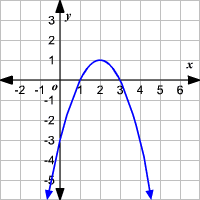
y = -(x-1)(x-3)
300
What is the line that splits the parabola in half called?
Axis of Symmetry
300
Solve:
y = x2 -14x + 49
x = 7
300
Graph the following function:
y = -(x - 1)(x+4)
The parabola should have:
Roots at (1, 0) and (-4, 0)
and a vertex at (-1.5, 6.25)
300
Graph the following function:
y = -x2 4x - 4
The parabola should have:
Root (2, 0)
and a vertex at (2, 0)
Y-intercept at (0, -4)
300
What the equation of the parabola:
With roots at (2, 0) and (-2, 0)
and a y-intercept of (0, -12)
y = 3(x+2)(x-2)
400
What is the value that show how wide or narrow a parabola is and if it open up or down?
"a" value
400
Solve:
y = 6x2 - 18x - 24
x = 4 and x = -1
400
Graph the following function:
y = 1/2(x - 4)(x+4)
Your graph should have:
Roots at (-4, 0) (4, 0)
Vertex at (0, -8)
400
Graph the following function:
y = 2x2 +10x - 12
The parabola should have:
Roots at (-6, 0) and (1, 0)
and a vertex at (-2.5, -24.5)
400
What the equation of the parabola:
With roots at (2, 0) and (6, 0)
and a y-intercept of (4, -1)
y= 1/4(x-2)(x-6)
500
What are the four names given to the points where the parabola crosses the x-axis?
Zeros
Roots
Solutions
X-intercepts
500
Solve:
y = 6x2 - 18x
x = 0 and x = 3
500
Graph the following function:
y = -x(x - 6)
The parabola should have:
Roots at (6, 0) and (0, 0)
and a vertex at (3, 9)
500
Graph the following function:
y = 1/2x2 -2x - 6
The parabola should have:
Roots at (6, 0) and (-2, 0)
and a vertex at (2, -8)
500
Write the equation of a parabola with zeroes at (4,0) and (2,0) and a y-intercept is at (0,1).
y=-1/8(x-4)(x-2)