What is the transformation rule for
f(x) + k
shift up "k" units
This Graph is the parent function for ___________.
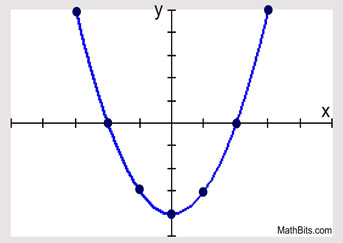
x2
What is the domain and range for the quadratic function?
D: (-∞, ∞)
R: [0, ∞)
What is Domain and how is it read?
x-values; Left to Right
What is the parent function for this equation?
f(x) = 2|x|+3
absolute value function
What is the transformation rule for
f(x - h) ?
shift right "h" units
This Graph is the parent function for ___________
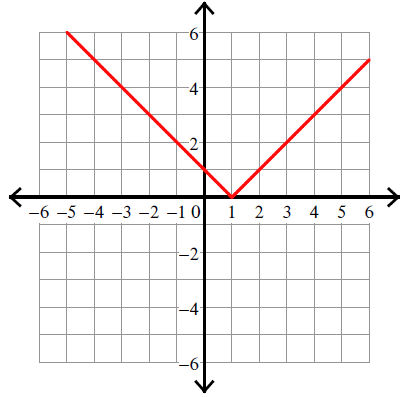
|x|
What is the domain and range for the absolute value function?
D: (-∞, ∞)
R: [0, ∞)
What is Range and how is it read?
y-values; Bottom to Top
y=-2x2-9 opens in the direction.
What is opens downward?
What is the transformation for the function: f(x) = 2|x|
Vertical Stretch by 2
The Graph the parent function is for _______.
√x
What is the domain and range for the cubed function?
D: (-∞, ∞)
R: (-∞, ∞)
What is a transformation?
An addition to the parent function that changes it is in some way
What is the vertex for this equation?
f(x) = x2+5
(0, 5)
What is the transformation of the graph f(x) = -x3 + 8
Reflection over x-axis, shift up 8
The Graph is the parent function for _______.

x3
What is the domain and range for the square root function?
D: [0, ∞)
R: [0, ∞)
What are the two types of Exponential Functions?
Growth and Decay
Vertex and axis of symmetry of y=2(x-3)2+5.
What is v(3, 5) and x=3.
What is the transformation of the graph f(x) = 1/2 (x+4) - 5
Vertical Compression by 1/2 ; Horizontal Shift by -4 ; Vertical Shift by 5
The parent function for this graph is named ______.
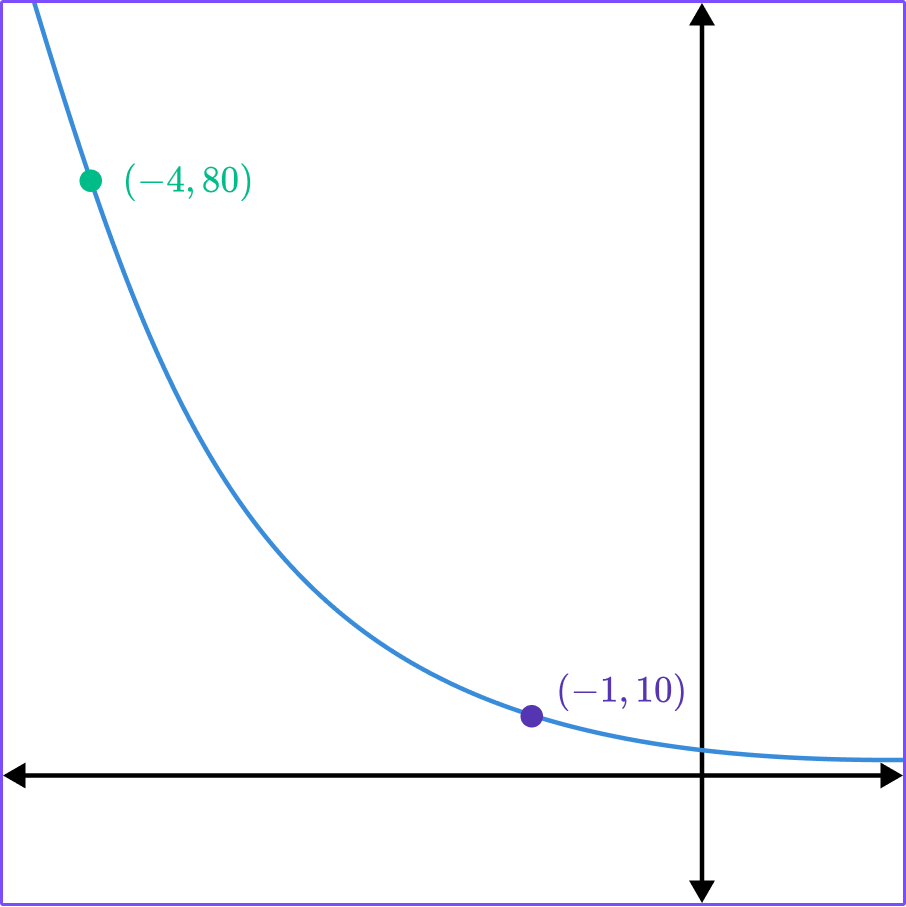
Exponential
What is the domain and range for a linear function?
D: (-∞, ∞)
R: (-∞, ∞)
123321 or Hannah is called.
What is a palendrome?
What determines whether an Exponential Function is growth or decay?