Linear Equation: Double Intercept Form / Standard Form
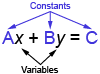
A linear equation in the form in the form Ax+By=CAx+By=C, where aa, bb, and cc are constants. The x- and y- intercepts are quickly to determined by setting the other variable to 0.
Example.
2x+3y=62x+3y=6
Point-Slope Form
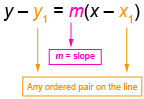
A linear equation in the form y–y_1 = m(x–x_1)+by–y1=m(x–x1)+b, where mm is the slope, bb is the y-intercept, and (x_1, y_1)(x1,y1) is any point on the line.
Example.
y+4=\frac{1}{3} \left( x-2 \right)y+4=31(x−2)
System of Linear Equations
A set of two or more equations with the same set of variables, or unknowns. The solution is the intersection of the lines.
Example.
2x + 4y = 102x+4y=10
5x - 6y = 125x−6y=12
What is the y-value of the solution to the system below?
x=\frac{7}{2}y+1x=27y+1
2x-4y= -12x−4y=−1
−1
One way to solve the system is to use substitution:
x=\frac{7}{2}y+1, 2x-4y= -1x=27y+1,2x−4y=−1
2(\frac{7}{2}y+1)-4y= -12(27y+1)−4y=−1
7y+2-4y= -17y+2−4y=−1
3y+2= -13y+2=−1
3y= -33y=−3
y= -1
y=−1
The cost of renting a car for one day is $40 plus $0.20 per mile. Which function below would represent this cost, C(m)?
C(m) = 0.20m + 40
Explanation:
This function represents an initial cost of $40 for the day plus 20 cents times the number of miles to equal the total cost, C(t).
Two painting companies charge for work completed with a linear equation, where C is Total Cost and t is time in hours worked. Company A charges C = 150 + 80tC=150+80t while company B charges C = 300 + 40tC=300+40t.
For 0 \leq t \leq 200≤t≤20, which of the following statements is true?
Company B charges more initially, but charges less per hour.
Explanation:
The initial charge is the y-intercept. Company B charges more initially ($300 while Company A charges $150 initially).
Company B charges less per hour ($40 per hour while Company A charges $80 per hour).
In the system of equations below, aa and bb are constants. If the system has infinitely many solutions, what is the value of the ratio \frac{a}{b}ba?
ax+by=12ax+by=12
2x+8y=602x+8y=60
41
Explanation:
In a linear system of equations with infinitely many solutions, the lines are the same (they have the same slope and y-intercept). One way to find the value of \frac{a}{b}ba is to solve the equations for yy and set them equal to one another.
Re-arranged for yy, The first equation is y=\frac{12}{b}-\frac{ax}{b}y=b12−bax; the second equation is y=\frac{15}{2}-\frac{1}{4}xy=215−41x.
Since the slopes of these two lines must be equal, -(\frac{a}{b})=-(\frac{1}{4}) \rightarrow \frac{a}{b}=\frac{1}{4}−(ba)=−(41)→ba=41.
Marta is raising money for a mission trip to Peru by selling flavored popcorn. She has rented a commercial popcorn machine and purchased various flavorings, popcorn kernels, butter, oil, and salt. So far, she has invested $225. She has determined that each 3-gallon container of popped corn costs $1.50 to make.
What is the cost of making 25 containers of popcorn
$262.50
Explanation:
Marta has invested $225 and each container costs $1.50 to make. Find the product of the cost to make each container and the number of containers and add this to her investment to get the total cost of making x containers of popcorn. The function f \left( x \right) =\$225+\$1.50xf(x)=$225+$1.50x represents the cost to make x containers of popcorn. Since x=25x=25, it follows that f \left( 25 \right) =\$225+\$1.50 \left( 25 \right) =\$262.50f(25)=$225+$1.50(25)=$262.50.
The equation y=4+1.5xy=4+1.5x describes the depth of the water, in y feet, of a pool being filled at the beginning of the summer after x hours. Choose the best interpretation of the y-intercept for this problem.
The y-intercept is 4 and describes the initial amount of water.
Explanation:
When x = 0, y = 4 so this is the y-intercept and describes the depth of the water that was in the pool before it began being filled for the summer.
After burning for 1 hour, a candle is 8 inches tall. After 3 hours it is 7.5 inches tall. Which of the following linear equations models the height of the candle y after x hours of burning?
y=−41x+841
Explanation:
The height of the candle, y, depends upon how long, x, it has been burning. Two points are represented by the information given in the problem: (1,8) and (3,7.5). The slope is m=\frac{8-7.5}{1-3}=-\frac{1}{4}m=1−38−7.5=−41. The equation that models the candle height versus time is y=-\frac{1}{4}x+by=−41x+b. Substitute the values of either point and solve for b: 8=-\frac{1}{4} \left( 1 \right) +b \rightarrow b=8\frac{1}{4}8=−41(1)+b→b=841.
What is the solution to the system of equations below?
-4x+3y=-5−4x+3y=−5
y=x-1y=x−1
(2, 1)
Explanation:
Substitution is the easiest method to use to solve this system because one equation has a variable that is isolated. The y variable is isolated in the second equation, which tells us that y is the same as x - 1. This means that the y in the first equation can be replaced with x - 1. Substitute using parentheses as follows: -4x+3 \left( x-1 \right) =-5−4x+3(x−1)=−5. Use the distributive property on the left side: -4x+3x-3=-5−4x+3x−3=−5. Combine like terms: -x-3=-5−x−3=−5. Add 3 to both sides to isolate x: -x=-2−x=−2. Divide both sides by -1 to isolate x: x=2x=2. Substitute 2 for x in the second equation: y= \left( 2 \right) -1=1y=(2)−1=1. Write the solution as an (x, y) ordered pair: (2, 1).
Which of the following is not an appropriate step of student work when solving the problem below?
2x+y=52x+y=5
-3x+6y=0−3x+6y=0
A
B
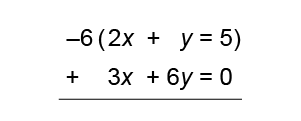
Option b is the wrong answer.
Explanation:
This is the beginning of the process for solving systems of equations by elimination.
C
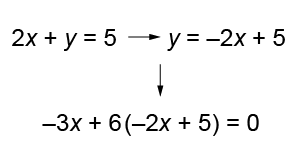
D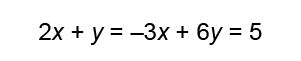
Option d is the correct answer.
Explanation:
Setting the equations equal to each other is not an appropriate way to solve a system of equations.