Who discovered Pi?
What is the 4th digit of pi? (after decimal)
5
3.141592653589
What is the formula for the area of a circle?
A = π x r x r
A = π r2
A circle has a radius(jari-jari) of 7 cm. Then the circumference of the circle is... cm.
Circumference of the circle (keliling) = 2 x Л x r
= 2 x 22/7 x 7
= 2 x 22
= 44 cm.

If the Radius of the circle is O-B: 14cm
Find the area of the shaded area.
Area of Circle
L = πr2
L = (22/7) . (14 cm)2
L = 616 cm2
Area of AOB:
AOB Area /area of circle = center point/360°
AOB Area /616 cm2 = 90°/360°
AOB Area /616 cm2 = ¼
AOB Area = ¼ . 616 cm2
AOB Area = 154 cm2
Triangle area of ∆AOB
L = ½ . base . height
L = ½ . 14 cm . 14 cm
L = 98 cm2
Shaded area AB:
Shaded area = AOB Area – Triangle area
Shaded area = 154 cm2– 98 cm2
Shaded area = 56 cm2
= 56 cm2
Who discovered the first 16 digits of Pi?
Isaac Newton
What is the 7th digit of pi? (after decimal)
6
3.1415926
State what profession/job can Pi be used for.
Your answer is:
A circular bucket lid has a circumference(keliling) of 154 cm. Then the radius(jari-jari) of the bucket lid is .... cm
(Circumference/keliling) = 2 x Л x r
154 = 2 x Л x r
154 : 2 = 22/7 x r
77 = 22/7 x r
77 : 22/7 = r
77 x 7/22 = r
r = 24,5 cm.

P is the center of the circle and the area of the sector (Juring) PLM = 24 cm². The area of the PKN section is?
Calculate the area of the circle by using this relationship:
The area of Sector (Juring) = ∠center / 360° × area of circle
area of PLM = ∠PLM/360° × area of circle
24 cm = 45°/360° x area of circle
area of circle = 360o/45o x 24
area of circle = 192 cm
Input all the values to calculate PKN :
area of PKN = ∠PKN/360° × area of circle
area of PKN = 60°/360° × 192
area of PKN = 32 cm2
Who discovered the diameter ratio of 355/113?
Zu Chongzhi
What is the 9th digit of pi? (after decimal)
3
3.141592653
What are the two forms of Pi?
3.14 and 22/7
What is the length of an arc of a circle with an angle of 72o and a radius of 10 cm?
In order to calculate the arc length of the circle, we need to calculate the circumference first. So we got:
Arc length = Circle circumference × Degree/360o
Arc length = 2πr×72o/360o
Arc length = 2 x 3,14 x 10 × 1/5o
Arc length = 12,56 cm

OP= 28
PQ=17.6
POQ=.......
Circumference of the Circle
K = 2πr
K = 2 x (22/7) x 28 cm
K = 176 cm
Area of the Circle
L = πr2
L = (22/7) x (28 cm)2
L = 2464 cm2
Degree value of POQ
∠ POQ /∠ 1 circle = length of PQ/circle circumference
∠ POQ /360° = 17,6cm/176 cm
∠ POQ = (17,6 cm/176 cm) x 360°
∠ POQ = 36°
POQ/Luas Lingkaran = ∠ POQ/∠ 1 lingkaran
POQ/2464 cm2 = 36°/360°
POQ = 0,1 x 2464 cm2
POQ = 246,4 cm2
Who has calculated the area of a circle by taking the value of Pi equal to 3? (according to history)
Babylonians
What is the 11th digit of pi? (after the decimal)
8
3.14159265358
Is Pi an infinite number?
No. Pi is Finite
If a circle has an area(luas) of 3,850 cm², then the radius(jari-jari) of the circle is...
(area of the circle) = Л x r²
3.850 = 22/7 x r²
3.850 : 22/7 = r²
3.850 x 7/22 = r²
3.850 : 22 x 7 = r²
175 x 7 = r²
r² = 1.225
r = √1.225
r = 35 cm.
The area of the shaded section (tembereng) in the following figure is...

The area of the Section (temebereng) can be defined by the following equation:
Section (tembereng) area = Wedge (juring) area - triangle area
Section (tembereng) area = 1/4.π.r² - 1/2.a.t
Section (tembereng) area = (1/4 x 22/7 x 212) - (1/2 x 21 x 21)
Section (tembereng) area = (21/2 x 33) - (21/2 x 21)
Section (tembereng) area = 21/2 x (33 - 21)
Section (tembereng) area = 21/2 x 12
Section (tembereng) area = 21 x 6
Section (tembereng) area = 126 cm2
Who used the value 3.16045, or 256/81 for pi?
What is the 20th digit of pi? (after decimal)
6
3.14159265358979323846
Can the circumference of a circle calculated be 100% accurate?
No, the accuracy of pi is 0.04% using the regular two format values of pi. It can't be 100% accurate but using the first 39 digits of pi can be considered atomically accurate. In hindsight, we don't need to know the EXACT value of pi.
Find the value of the grey-shaded area. (in cm2)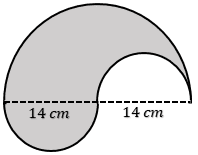
Itu artinya luas daerah yang diarsir = Luas setengah lingkaran besar saja
dengan r = 14 cm
= ½.π.r²
= 1⁄2 x 22⁄7 x 14 cm x 14 cm
= 1⁄2 x 22⁄1 x 14 cm x 2 cm
= 1⁄1 x 11⁄1 x 14 cm x 2 cm
= 11 x 14 cm x 2 cm
= 308 cm²

ABCD is a square with a side length of 50 cm. Inside, there is a circle. The area of the yellow-shaded part is?
The diameter of the circle is the same as the side of the square.
square side = d
d = 50 cm
radius = 25 cm
Calculate the area of circle = Л x r²
area of the circle = 3.14 x 252
area of the circle = 1962.5 cm
In the circle, there are two triangles. When those two triangles are combined, it will create a square that has the same side as the radius.
small square side = radius
r = 25 cm
area of small square = side x side
area of small square = 252
area of small square = 625 cm
Input the values and calculate the yellow area, we got:
area of the circle - the area of the small square
= 1962.5 - 625
= 1337.5 cm2