Working those Abs..olute Values
Quadratic Key Features
Solving Quadratics
Writing Quadratic Equations.
100
The vertex form of an absolute value equation is shown below. The value of a reveals two key features.
y=a|x-h|+k
What is direction (opens up/down) and the slopes of the sides.
100
The vertex form of a quadratic equation is given below. What UNIQUE key feature is given from this equation?
y=a(x-h)^2+k
What is the Vertex?
100
Solve for x.
-(x+4)(x-1)=0
x = -4
x = 1
100
What does factored form look like?
y=a(x-p)(x-q)
200
What is the vertex of this absolute value function?
g(x)=-2|x+4|+3
(-4, 3)
200
What is the vertex of the quadratic function.
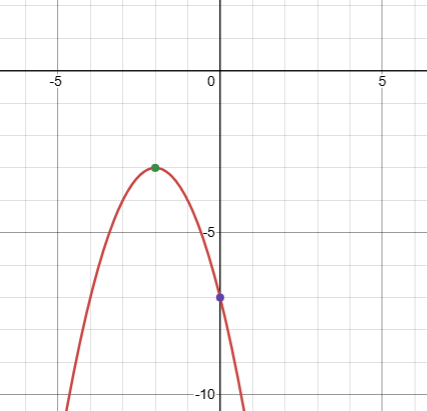
(-2, -3)
200
Solve for x.
x^2-8x+16=0
x = 4
200
Rewrite this equation in standard form:
y=3(x+1)(x-5)
Standard form:
y=ax^2+bx+c
y=3x-12x-15
300
How many solutions does this equation have?
-|x+7|-14=12
zero
or no solutions
300
What is the y-intercept of the following quadratic equation?
f(x)=-2x^2+5x-7
(0, -7) or -7
300
Solve for x.
-2(x+1)^2-4=-8
x = 1, -1
300
Rewrite this equation in factored form.
y=-x^2-x+6
Factored form:
y=a(x-p)(x-q)
y=-(x+3)(x-2)
400
Solve the following absolute value equation.
5=|x-3|-25
x = 33 and x = -27
400
What is the vertex of the following quadratic function?
y=-5(x+4)^-7
(-4, -7)
400
Solve for n.
-3n^2-12n+6=-9
n = -5, 1
400
Write the equation of the quadratic that has the x-intercepts (4, 0) and (-1, 0) and goes through the point (3, 8) in factored form.
y=-2(x-4)(x+1)
500
List the key features from this absolute value function. y=2|x+1|-5
Vertex:
Direction:
Slopes of sides:
Vertex: (-1, -5)
Direction: Opens upward
Slopes of sides: +2, -2
500
What are the x-intercepts of the quadratic function? Hint, use quadratic formula or factor.
y=2x^2+4x-6
(1, 0) and (-3, 0)
500
Solve for x.
2(x+4)^2+5=-3
No solution!
500
Write the equation of the parabola that has a vertex at (5, -2) and goes through the point (3, 6). This equation needs to be in vertex form.
Vertex form:
y=a(x-h)^2+k
y=2(x-5)^2-2
600
Solve the absolute value equation:
|x/4+1|-4=-4
x=-4
600
On what interval of x is our graph positive?
y=-(x+1)(x-4)
-1<x<4
600
solve for x.
-x^2-13x+15=45
x = -10, -3
600
What is the equation of the parabola that has the x-intercepts of (-7, 0) and (1, 0) and goes through the point (-6, 7).
Write this equation in standard form
y=ax^2+bx+c
y=-x^2-6x+7
700
What is the equation of the absolute value function shown?
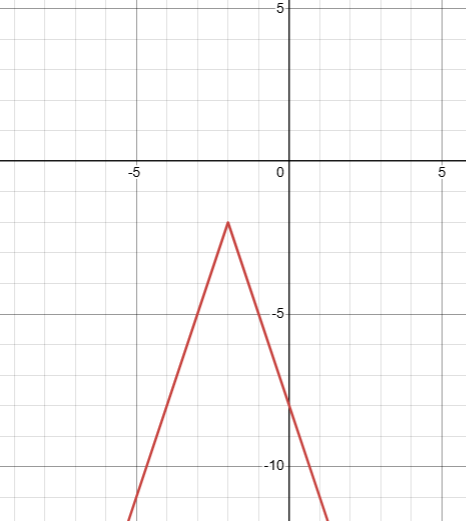
y=-3|x+2|-2
700
On what interval of x is this graph increasing?
y=-x^2-8x-16
x<-4
700
Solve for x.
-10x^2-x-4=-7
x = 1/2, -3/5
700
Convert this equation from standard form to vertex form.
y=2x^2-4x+5
y=2(x-1)^2+3