La variable de
-2x^2 + 5x - 4
est
x
(2x^2 - 3y) + (2x^2 - 5y)
4x^2 - 8y
(-5y - 2) - (11y - 8)
-16y + 6
−3(−4a^3 −4a − 9)
12a^3 + 12a + 27
(-42x^2 + 7) ÷ -7
6x^2 - 1
Le type de ce polynôme:
3y^5 + 3x^3y^3 + 2
trinôme
(-5x^3 + 2x - 9) + (x^3 - 4x + 1)
-4x^3 - 2x - 8
(mn^2 - m + 1) - (n^2m + m - 1)
-2m + 2
−2x(x^2 − 3x − 4y + 2)
−2x^3+ 6x^2 + 8xy − 4x
(13x^2 + 2x^2 − 5x)/5
3x2 - x
Ce polynôme en ordre décroissant:
2x^5 + 5x^6 - 4 + 2x
5x^6 + 2x^5 + 2x - 4
(-ab^2 + 3ab + 2) + (4 - 5ba + ab^2)
-2ab + 6
-(3x^2 - 4x + 3) - (-x^2 + 8x - 3)
-2x^2 - 4x
−n^2m^3 (−2m^4n + 4m^3 − n + 3)
2m^7 n^3 − 4m^6 n^2+ m^3 n^3 − 3m^3 n^2
(80m^3 n^2 − 40m^2 n) ÷ −20mn
−4m^2 n+2m
Le terme constant de
-2x^5y^7z - 19 + 5x^9y - 6x^4y^5z^2
est
-19
Détermine le périmètre: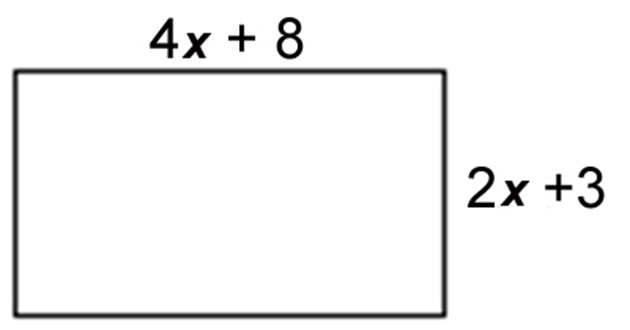
12x + 22
Détermine le côté qui manque si le périmètre est 11x+4
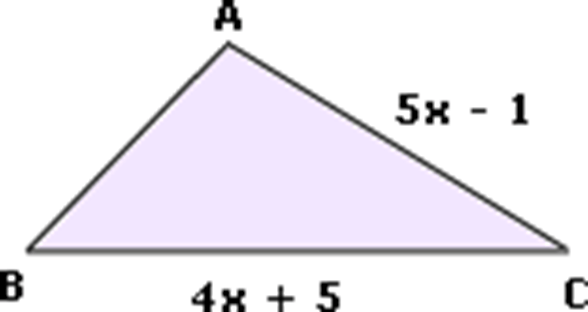
2x
2b(3b^2 + 4 - 2b + 6)
6b^3 - 4b^2 + 20b
(−12a^4 b + 4ab − 8ab + 4a^4 b)/(−4ab)
2a^3+ 1
Les coefficients de
-x^4 + 4y + y^2 - 3 - 7x
sont
-1, 4, 1, -7
Remplis:
(-2a^2 + 5a - 2) + (.......) = -5a^2 - 2a + 6
-3a^2 - 7a + 8
Remplis:
(-5b^2 + 4b - 11) - (.......) = b^2 - 1
-6b^2 + 4b - 10
(2x - 5)(3x + 8)
6x^2 + x - 40
(−80a^4 b^2 c −10ab^5 c −a^4 b^2 c + b^5 ac) ÷ (9ab^2 c)
−9a^3 − b^3