Classify
End Behavior
Even/Odd Symmetry
Extrema
Intervals of Inc/Dec
100
Classify the polynomial below:
f(x) = -2x4 - 5x2 + 3x - 10
Quartic Polynomial
100
If a polynomial's end behavior is the same, the function has this type of degree.
Even polynomials
100
Explain the difference between the following and what they can tell you about a graph:
- even/odd functions
- even/odd degree
- symmetry
- end behavior
100
What is an extrema?
turning points of a polynomial; maximum and minimums
100
identify ONE interval of increase of the polynomial:
f(x) = x4+3x3-4x
(-2, -0.8) OR (0.6, infinity)
200
Classify the polynomial below:
f(x) = 10x3 + 3x - 10
Cubic Polynomial
200
If the polynomial is odd, then this happens to the end behaviors
they go to both positive and negative infinity
200
Create an example of a polynomial that...
- is even
- has even degree
(to be checked)
200
identify ONE extrema of the polynomial below:
f(x) = -x3-7x2-15x-9
Label the point as (relative min/max, absolute min/max) and the ordered pair.
Relative (local) max: (-1.7, 1.2)
Relative (local) min: (-3,0)
200
identify ONE interval of decrease of the polynomial: f(x) = x4+3x3-4x
(-inf, -2) OR (-0.8, 0.6)
300
Classify the polynomial below:
f(x) = x5+7x4+10x3-18x
Quintic Polynomial
300
If the polynomial is even and the leading coefficient is negative then the end behaviors...
both go to negative infinity
300
Even functions are symmetric over the ...
Odd functions are symmetric over the ...
y-axis
origin
300
identify ONE extrema of the polynomial below:
f(x) = -x4 + 3x3 - 2x
Label the point as (relative min/max, absolute min/max) and the ordered pair.
Abs Max: (2.1, 4.1)
Rel (local) Max: (-.4, .5)
Rel (local) Min: (.5, -0.7)
300
identify ONE interval of increase of the polynomial:
f(x) = x3+4x2+4x
(-inf, -2) OR (-0.7, inf)
400
Classify the polynomial below:
f(x) = x2-3x-10
Quadratic Polynomial
400
Determine the end behavior of the polynomial below:
- 4x3 + 2x2 + 3
x-> infinity, y-> negative infinity
x-> negative infinity, y-> infinity
400
Even, odd, or neither
f(x) = 6x16 - 10x6 - 3
even
400
identify ONE extrema of the polynomial below:
f(x) = x3+2x2-11x-12
Label the point as (relative min/max, absolute min/max) and the ordered pair.
relative max: (-2.694, 12.597)
relative min: (1.361, -20.745)
400
identify the interval of decrease of the polynomial:
f(x) = x3+4x2+4x
(-2, -0.7)
500
How do you find the degree of a polynomial?
By looking at the first term and the power associated with it
500
Determine the end behavior the of the polynomial below:
y = -3x2 + 4x + 1
x -> infinity, y -> negative infinity
x -> negative infinity, y -> negative infinity
500
What type of function is this? Classify with even /odd degree and symmetry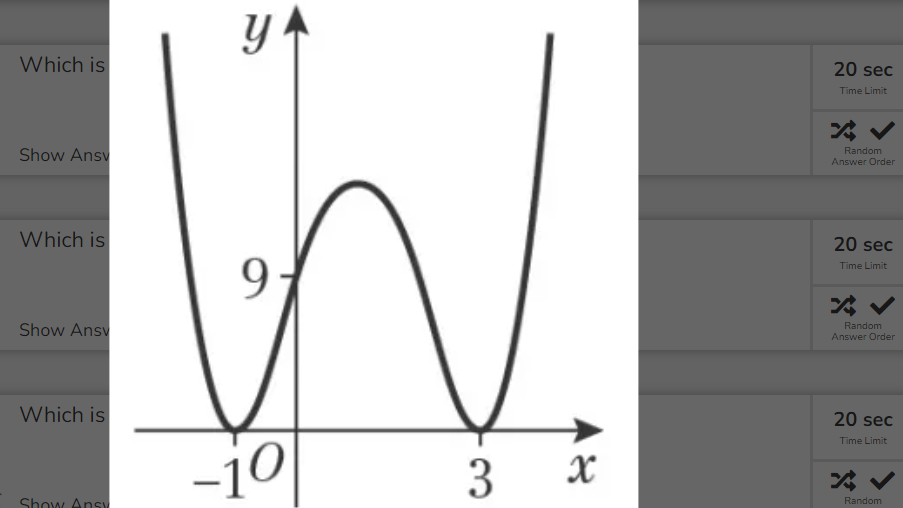 
neither even nor odd
500
identify ONE extrema of the polynomial below:
f(x) = x4+11x3+36x2+16x-64
Label the point as (relative min/max, absolute min/max) and the ordered pair.
Abs min: (-0.3, -65.9)
500
identify the increasing and decreasing interval of the polynomial:
f(x) = x4+6x3+12x2+8x
dec: (-inf, -0.5)
inc: (-.5, inf)