Test I
Test II
Test III
Test IIII
100
In a Quadratic Function, if the value of a is positive, then it opens ______.
UPWARD
100
It is the minimum point of graph of quadratic function.
VERTEX
100
What is the last step in graphing polynomial?
LABEL THE GRAPH
100
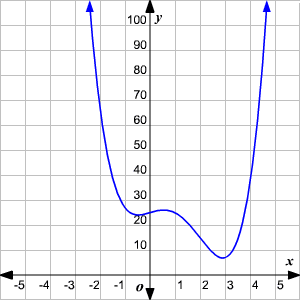
What is the end behavior of the graph below?
It both falls down to the left and to the right
200
Find the y-intercept of the function.
y= x2-2x+ 1999
y= 1999
200
Find the x-intercept or zeroes of the function.
y=3x + 12
0= 3x + 12
-12 = 3x
x= -4
(-4,0)
200
Classify by degree of polynomial:
3x2- 8x + 1
QUADRATIC
200
f(x) = (x+4)(x-3)(x-2)
List the zeroes for this function.
x=-4, x=3, x=2
300
It is a polynomial that has a degree of 3
CUBIC
300
What is the end behavior of the graph
It rises to the right then fall to the left
300
Given this polynomial function: y= 2x3-7x2-7x+12
What is the behavior of it's graph?
A. Left hand : falling , Right hand: rising
B. Left hand : falling , Right hand: falling
C. Left hand : rising , Right hand: falling
A. Left hand : falling , Right hand: rising
300
Find the intercepts of
y= x4+ 6x3-x2-6x
y= x4+ 6x3-x2-6x
y= x(x+6)(x+1)(x-1)
0= x(x+6)(x+1)(x-1)
400
Which best describes the graph of the function
f(x)= x3+3x2-4x-12?
A. It is shaped like a letter U with its sides sloping outward.
B. It goes down to the far left and up to the far right. C. It goes down to the far left and down to the far right.
B. It goes down to the far left and up to the far right.
400
What are the factors of this polynomial function?
P (x) = - x3 - x2 + 2x.
P (x) = - x3 - x2 + 2x
= - x (x2 + x - 2)
= - x (x + 2)(x - 1)
400
Factor polynomial P given by
P (x) = x4 - 2x2+ 1
- P (x) = x4 - 2 x2 + 1
= (x2 - 1) - = ((x - 1)(x + 1))2
- = (x - 1)2 (x + 1)2
400
What is the end behavior of the graph below
It rises to the right the fall to the left
500
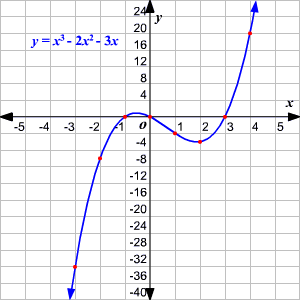
Graph the polynomial function x3−2x2−3x
500
GIVE THE 6 STEPS IN GRAPHING POLYNOMIAL.
1. Determine the graph and behavior
2. Find the x-intercept or zeroes of the function.
3. Find the y-intercept of the function.
4. Find the number of maximum turning points.
5. Draw the graph.
6. Label the graph.
500
Graph the polynomial p(x) = (x-3)(x+2)(x+5).
500
Find the end behavior of the function x4−4x3+3x+25
