A number, variable, or a product of a number and a variable in a polynomial that is separated by an addition or subtraction sign is called a ...
a term
The degree of this polynomial:
x3 - 7x2 + 4x5y2 - 19x7y
- 19x7y1
Add the exponents from the variables 7 + 1 = 8
Final Answer = 8
Add the Polynomials
(4x - 9) + (x + 4)
5x - 5
Add the following polynomials
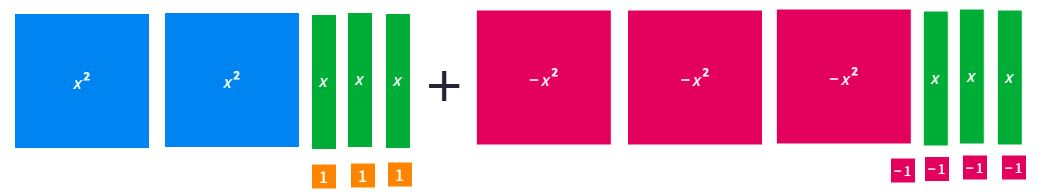
-x2 + 6x - 1
-9x(4x-7)
-36x2+63x
Find the perimeter of the rectangle.
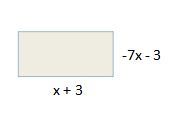
(-7x - 3) + (-7x - 3) + (1x+3) +(1x+3)
= (-7x - 7x + 1x + 1x) + (-3 - 3 + 3 + 3)
Final Answer = -12x
The number before a variable within a term is called the...
Coefficient
Combine like terms and write in standard form
2x - 2 + 3x2 - 5
3x2 + 2x - 7
Add the polynomials:
(-3a - 12) + (7a + 5)
4a - 7
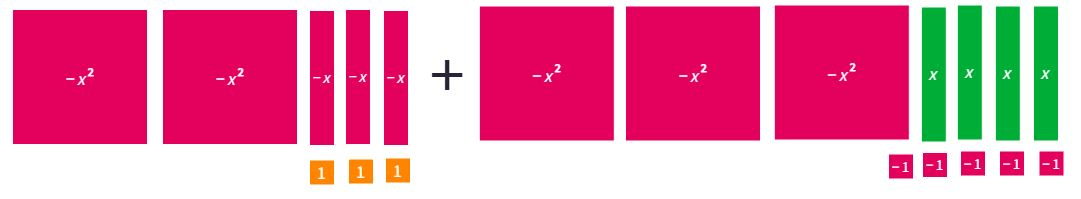
-5x2 + x - 2
(x-3)(x-9)
x2-9x-3x+27
Final Answer: x2-12x+27
Find the perimeter of the isosceles triangle.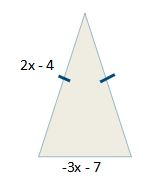
The tic mark means the sides are the same length.
(2x-4) + (2x-4) + (-3x-7)
Final Answer: x - 15
The number in front of the term with the highest degree.
Leading Coefficient
A quadratic polynomial has a degree of this.
2
Subtract the polynomials:
(-x2 - 5) - (-3x2 -x -8)
(-1x2 - 5) + (3x2 + 1x + 8)
Final Answer: 2x2 + x + 3
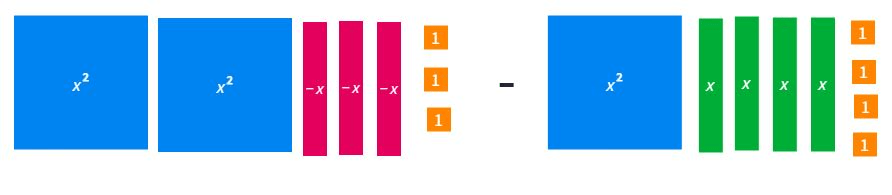
x2 - 7x - 1
Multiply the Polynomials:
3x2 (2x5 + 6y)
6x7 + 18x2y
What is the area of the rectangle below?
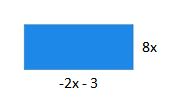
Area = length x width
= (-2x-3)8x
Final Answer = -16x2 - 24x
When you add the exponents of each of the variables of each term and found the highest one you found the...
Degree of the term
Polynomials are closed under which operations?
Adding 2 polynomials will always result in another polynomial.
Subtracting 2 polynomials will always result in another polynomial.
Multiplying 2 polynomials will always result in another polynomial.
So Adding, Subtracting, and Multiplying are closed
Subtract the Polynomials:
(k2 + 6k3 -4) - (5k3 + 7k -3k2)
Change to addition problem and combine like terms.
(1k2 + 6k3 -4) + (-5k3 - 7k +3k2)
k3 + 4k2 -7k - 4
Subtract the Algebra Tiles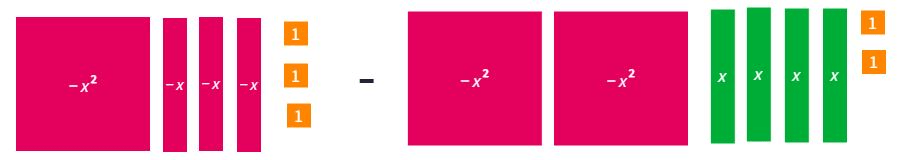
x2 - 7x + 1
(2x-3)(2x+3)
4x2 +6x - 6x - 9
Final Answer: 4x2 - 9
Find the perimeter of a rectangle whose length is (5x - 4) inches and width is (6x + 2) inches
(5x - 4) + (5x - 4) + (6x + 2) + (6x + 2)
Final Answer = (22x - 4) inches
Terms that have the same variables and the same degree are called ...
Like terms
Which of the following are examples of a monomial?
a) 2x - 3x
b) 3x - 9y
c) 9x2 - 2x
d) 1 + 2 + 9
A) 2x - 3x = -1x
and
D) 1 + 2 + 9 = 12
Subtract the Polynomials:
(2x2 - 3x) - (x2 -2x + 4)
Change subtraction to addition
(2x2 - 3x) + (-1x2 +2x - 4)
x2 - x - 4
Subtract with Algebra Tiles

-x2 + 10
(x-8)2
(x-8)(x-8)
x2 - 8x - 8x + 64
Final Answer: x2-16x+64
Find the area of a room that is
(3x - 5)feet by (2x + 1) feet.
(3x-5)(2x+1) = 6x2+3x-10x-5
Final Answer: (6x2 - 7x - 5) ft2