Vocabulary
Looking at graphs
Rational Functions and Asymptotes
Miscellaneous
100
another word for "root"
zero
or
x-intercept
100
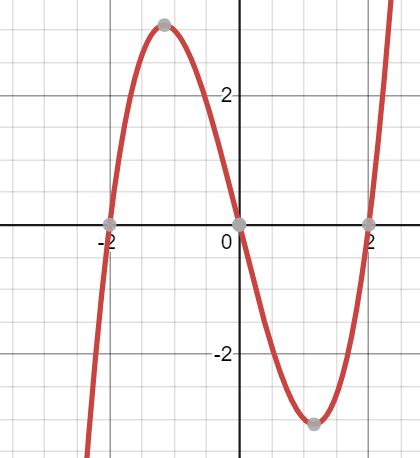
What are the roots of this function?
x=-2
x=0
x=2
100
If a rational function has a denominator of (x + 4), will it have:
a. a horizontal asymptote at y = 4
b. a horizontal asymptote at y = -4
c. a vertical asymptote at x = 4
d. a vertical asymptote at x = -4
d. a vertical asymptote at x = -4
100
Where was Usher at 7 o'clock on the dot?
In his drop top cruising the streets
200
definition of a rational function
a function in the form of a fraction, where the numerator and (especially) the denominator are both polynomials
200
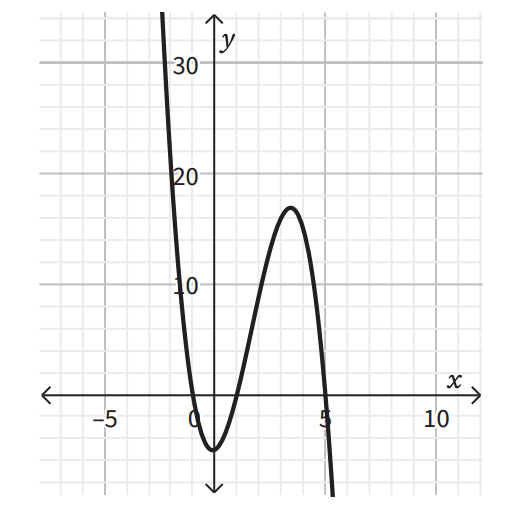Give a possible equation for this function. Hint: writing it in factored form is acceptable
f(x)=(x+1)(x-1)(x-5)
200
Why do rational functions have vertical asymptotes?
Because when you have a variable in the denominator, there are limitations to the function's domain. There are x-values that will make the denominator equal 0, and dividing by 0 is impossible!
200
describe the end behavior of the polynomial y = -10x34
as x gets very big, y gets very small
as x gets very small, y gets very small
300
definition of a polynomial
a function that may have multiple terms and whose exponents are all positive integers
300
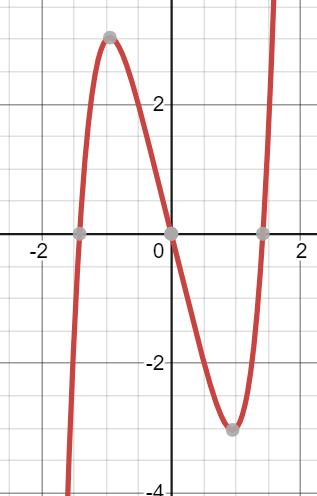
Give a possible degree and leading coefficient for this function
degree = odd and at least 3
leading coefficient = any positive number
300
Use the vertical asymptotes to write a possible denominator for this rational function. Factored form is okay.
denominator should include (x+1)(x-2)
300
In total, how many local minima and maxima (minimums and maximums) does this function have?
2 (the peak between x=5 and x=6 is the global maximum)
400
definition of 'degree'
the largest exponent of a polynomial
400
Describe the end behavior of this function. (The two most impressive answers will score points.)
Example:
As x approaches infinity, y approaches -infinity
As x approaches -infinity, y approaches infinity
400
What is the horizontal asymptote of the function
(2x - 3)/(x-4)
y = 2
400
What is Mr. Simonich's cat named?
Points go to the answer that is (a) closest to correct, and (b) funniest
Sophie
500
definition of a 'term'
A component part of a polynomial that includes a coefficient, a variable and an exponent. Terms are added together to create a polynomial
500
Does the graph above depict a polynomial? Why or why not?
Yes. It is a linear function which has a degree of 1: the exponent is omitted here for expediency but 1 is both positive and a whole number
500
What is the domain of the function 1/(x2+5x+6) ?
x is all real numbers except for -2 and -3
500
Rewrite this rational function in the form of a polynomial with a remainder.
x2 - 4 + (16/(x+2))