Factoring
Graphing Polynomial Functions
Dividing Polynomials
Imaginary/Complex #'s
Vocabulary
100
Factor x2+6x+9
(x+3)2
100
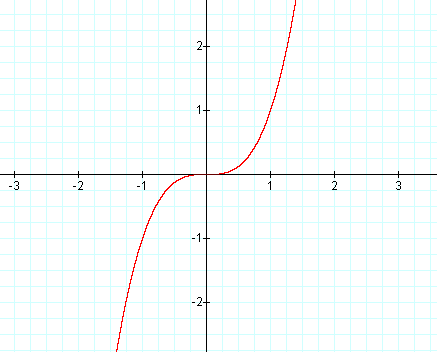
Sketch y=x3
100
x3-9x2+23x-15/x-5=?
=x2-4x+3
100
Simplify x2+25
x=5i or -5i
100
Define: The leading term of a polynomial function.
Definition: The term with the highest power of x. (Its coefficient is called the leading coefficient.)
200
Factor 4x2-36
4(x-3)(x+3)
200
If the leading term is negative. What happens to the end of the graph?
The graph ends negative. (if it was positive, the graph would end positive.)
200
15x3-2x2+11x-4/3x-1=?
5x2+x+4
200
(7+2i)-(5-6i)=?
= 2+8i
200
Define: Imaginary number
Definition: An imaginary number is a real number multiple of "i" (ex. 3i,4i,5i)
300
Factor 3x2-5x-2
(3x+1)(x-2)
300
If a polynomial function is the 6th degree how many "humps" will be on the graph?
5 humps
300
7x3-19x2+x+2/7x+2=?
=x2-3x+1
300
(-2+i)+(3-5i)=?
=1-4i
300
Define: The factor theorem
Definition: If x=b is a root of a polynomial function p(x), then x-b is a factor of p(x)
400
Factor 49x2-70x+25
(7x-5)2
400
f(x)=(x-3)(x2+5)(x-2)
Find the x and y intercepts
x intercepts - x=2 and x=3
y intercepts - y=30
400
x3+2x2+x+5/x+2=?
= x2+1+(3/x+2)
400
(3-5i)(3+5i)=?
34
400
Define: Rational root theorem
Definition: If a polynomial function. P(x) has linear factors then those factors are of the form ax-b. Where..
- B is a factor of the constant
- A is a factor of the leading term
- The corresponding root is x=b/a
500
Factor x4+2x3−7x2−8x+12
(x-1)(x+3)(x-2)(x+2)
500
f(x)=(3x-6)3(x+2)2(7x+12)
Find x and y intercepts
x intercepts - x=2, x=-2, and x=-12/7
y intercepts - -10368
500
3x4+2x2-x+6/x2+1=?
= 3x2-x+3+(-3x+3/x2+1)
500
(7+2i)(5-3i)=?
= 41-11i
500
Define The remainder theorem
Definition: if p(x) is a polynomial function, then the remainder of p(x)/x-b) is p(b).