Graphs
Synthetic Division
Using the Remainder Theorem and Factor Theorem
Random Polynomial Math
More Random Polynomial Math
Rational Functions
100
What degree is the following Polynomial:
4
100
The remainder is:
(4x^3+7x^2+3x+10)/(x+2)
0
100
Use the Remainder Theorem to find f(-2):
x3 + 4x + 2
-14
100
The zeros of a function represent these of a graph. (What are 3 other words for zeros?)
x-intercepts or roots or solutions
100
The degree of this polynomial:
x3 - 7x2 + 4x5 - 19x7
7
100
Give the equation of the vertical asymptote for f(x)=(2x+3)/(x-3).
What is: x=3 ?
200
What is the y- intercept?
y= x^3-4x^2-11x+30
30
200
The remainder is...
(4x^3+7x^2+3x+10)/(x-1)
24
200
Use the factor theorem to find the zeros for
f(x) = 2x3 + 2x2 - 8x - 8
What is: (-2, 0), (-1, 0), and (2, 0)
200
What is the end behavior of y=x2+2x-3x3-6
What is: Left Up, Right Down
200
How many zeros does this polynomial have? (BE SPECIFIC)
4 Zeros but x=3 is a bounce, so 5 total!
OR
3 real and 1 bounce (counts as 2)
200
Give the y-intercept for f(x)=(2x+3)/(x-3).
What is: (0, -1) ?
300
List the increasing and decreasing intervals of this graph.
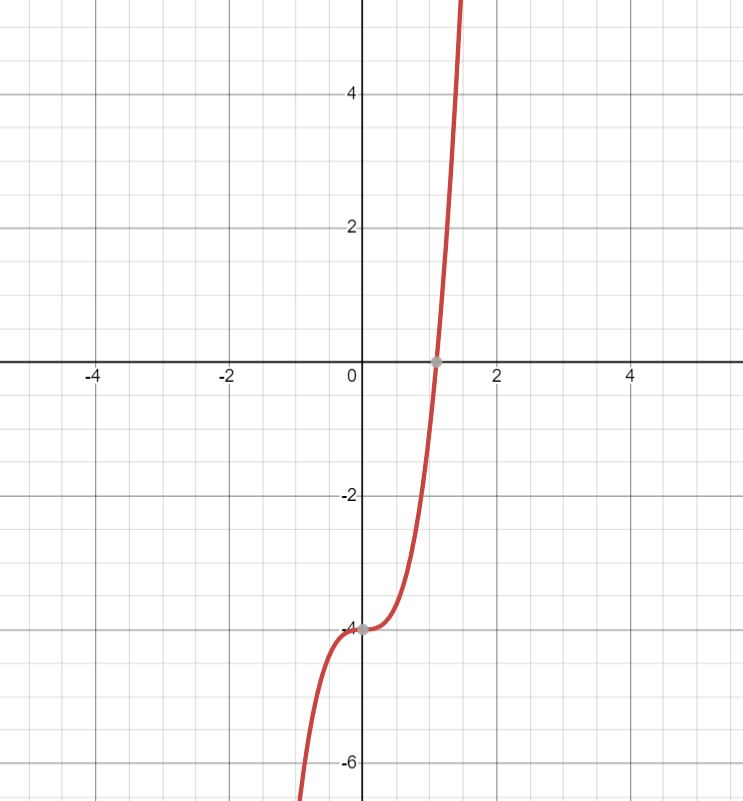
INC:
(-oo, 0 )
INC:
(0, 00)
300
The remainder is...
(-x^3+2x+3)/(x+1)
2
300
Use the Remainder Theorem to solve the following:
When y = x3 + kx2 − 4x + 2. is divided by x + 2 the remainder is 26, find k.
k = 6
300
What is the end behavior of y=2x6+7x3-6x+57
What is: Up, Up
300
Write a possible equation given the zeros:
x= 2, -1, 2/3 Write in factored form, no fractions
y=(x-2)(x+1)(3x-2)
300
State the horizontal asymptote for f(x)=(2x+3)/(x-3).
What is: y = 2 ?
400
What is the Domain and Range of the following graph:
Domain:
(-oo, oo)
Range:
(-oo, 3.644]
400
Solve. Write any remainder as a fraction.
(x^3-5x^2+8x+4)/(x-1)
x2-4x+4+8/(x-1)
400
Use the Factor Theorem to find the zeros of:
y = x3 - 4x2 - 15x + 18
(-1, 0), (4, 0), and (5, 0)
400
Find the zeros and their multiplicities of:
(x2-81)(x2+3x-10)(x-9)2
Zero: 9, Multiplicity: 3
Zero: -5 Multiplicity: 1
Zero: 2 Multiplicity: 1
Zero: -9 Multiplicity: 1
400
What is the Domain and Range of this Graph?
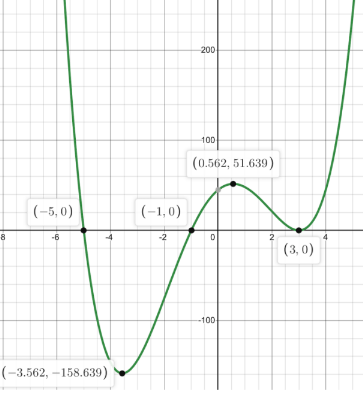
Domain: (-oo, oo)
Range:
[-3.562, oo)
400
State the x-intercepts for f(x)=(2x+3)/(x-3).
What is: (-1.5, 0) and (3,0)?
500
Write a possible equation for the graph
- (x+7)(x+2)(x-1)(x-5)
500
Solve. Write any remainder as a fraction.
(x^3+2x^2-5x+3)/(x+4)
x2-2x+3-9/(x+4)
500
Use the Rational Zero and Factor Theorems to find the zeros of
y = x3 - 3x2 - 6x + 8
(-2, 0), (1, 0), and (4, 0)
500
An odd function crosses through the coordinate point (2,3). What is another coordinate point that the graph MUST pass through?
(-2,-3)
500
Over what intervals is the function decreasing?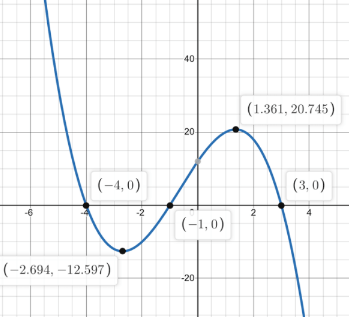 
(-oo, -2.694) U (1.361, oo)
500
State the type of discontinuity and the x-value at which it occurs for f(x)=(2x+3)/(x-3).
What is: infinite at x=3