Attributes of Graph
Evaluating Functions
Triangle Trigonometry
Unit Circle
Trig graphs/transformations
100
Determine the global maximum and minimum value of the function f?
What is Global maximum of 3 at x = 5
What is Global minimum of 2.3 at x=0
100
Given f(x) = 8x+9, find f(7).
A.) 60
B.) 63
C.) 65
D.) 68
What is C.) 65
100
Write formulas for sin, cos, tan.
What is Sin: Opposite/Hypotenuse
Cos: Adjacent/Hypotenuse
Tan: Opposite/Adjacent
100
Write the equation represented by the graph.
A.) y=sinx
B.) y= cosx
C.) y = sin^-1 x
D.) y = cos^-1x
What is B.) y = cosx
100
According to the unit circle, in which 2 quadrants is tangent always positive, and which 2 quadrants is sin negative?
A) tan + = II & IV, sin - = III & IV
B.) tan + = I & III, sin - = III & II
C.) tan + = I & IV, sin - = I & III
D.) tan + = I & III, sin - = III & IV
What is D.) tan + = I & III, sin - = III & IV
200
The graph of the function f(x) is shown below. Determine all jump discontinuity?
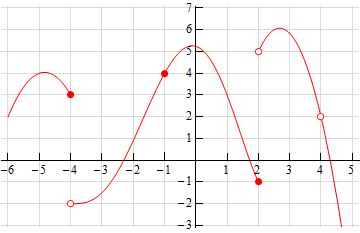
A). x = -1, X = 4
B). x = -4, x = 2
C). x = 3, x = 5
D) x = -2, x = -1
What is B). x = -4, x = 2
200
Given f(x) = 8x²+2x-10, and g(x)= x+19, find the value of g(f(-2)).
Write it in polynomial (simplest form).
A.) 37
B.) 40
C.) 50
D.) 29
What is A.) 37
200
Solve for the missing side (x) of the right triangle.
A.) 35.5
B.) -31
C.) 29.2
D.) 30.2
What is D.) 30.2
200
Determine what is the period. y = 177sin (80πt - π/3)
A.) 40
B.) 2/40
C.) 1/40
D.) 30
What is C.) 1/40
200
find all angles, 0° ≤ θ < 360°, that solve the following equation. sin(x) = -1/2
A.) x = 30° & 150°
B.) x = 135° & 225°
C.) x = 210° & 330°
D.) x = 45° & 315°
What is C.) x = 210° & 330°
300
Decide if the following function is even, odd, or neither?
f(x) = x⁵ + 4x⁵
A). Even
B). Neither
C). Odd
What is C.) Odd
300
Solve for g(f(g(f(-3))))
f(x) = x+6
g(x) = 6/x
A.) 0.55
B.) 0.75
C.) 0.45
D.) 0.85
What is B.) 0.75
300
Calculate the measure of the missing angle.
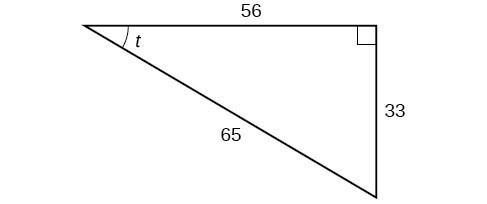
A.) 30.5°
B.) 40°
C.) 65.7°
D.) 70°
What is A.) 30.5°
300
For the rotation 1040, find the coterminal angle from 0∘≤θ<360∘, the quadrant, and the reference angle.
The coterminal angle is ___°, which lies in Quadrant ___, with a reference angle of ___°.
What is the coterminal angle is _320__°, which lies in Quadrant _IV__, with a reference angle of _40__°.
300
Simplify to a single trig function.
sec^2 θ ⋅ cot^2 θ
A.) sin^2 θ
B.) csc^2 θ
C.) sec^2 θ
D.) cos^2 θ
What is B.) csc^2 θ
400
Write the equation for the piecewise function.
What is 2x-3 for x < -2
x-1 for -2 ≤ x < 3
-1/3x+4 for x ≥ 3
400
Given f(x) = x²+20x+8, and g(x)= 3x+5, find f(x) ∘ g(x).
Write it in polynomial form (simplest form).
A.) 50x²+22x+5
B.) 65x²+124x+40
C.) 6x³+60x²+100x+20
D.) 3x³+65x²+124x+40
What is D.) 3x^3+65x²+124x+40
400
Solve for c using Law of Sine.
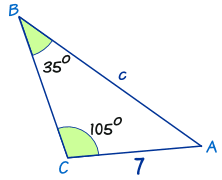
A.) 14.4
B.) 7.5
C.) 11.79
D.) 12.29
What is C.) 11.79
400
Find the exact value of sec 5π/6 in simplest form.
A.) -4√3/3
B.) -2√3/3
C.) 2√3/3
D.) 4√3/3
What is B) -2√3/3
400
Solve the trigonometric equation.
4sin^2x - 3 = 0
A.) 2π/3, π/3, 4π/3, 5π/3
B.) 5π/6, π/3
C.) 2π/3, π/3, 5π/6, π/6
D.) 2π/3, 5π/3
What is A). 2π/3, π/3, 4π/3, 5π/3
500
Determine the following features.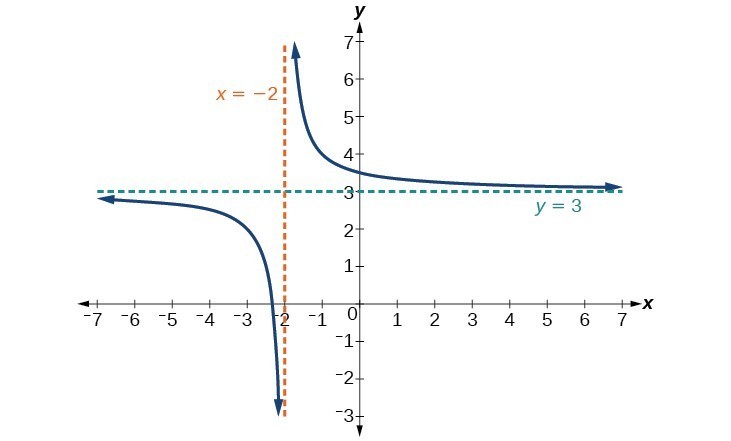
1.) Discontinuity
2.) End behaviors
3.) Domain & Range
4.) Asymptotes
What is
Discontinuity: Infinite discontinuity at x=-2
End Behaviors: As x --> -∞, f(x) --> 3
As x--> ∞, f(x) --> 3
Domain: ( -∞, -2) U (-2, ∞)
Range: ( -∞, 3) U (3, ∞)
Asymptotes: VA: -2
HA: 3
500
Find the inverse of f(x)= 4x-7/9x
A.) -6/5x-4
B.) -7/9x+4
C.) -6/5x+4
D.) -7/9x-4
What is D.) -7/9x-4
500
Alicia is flying a kite, holding her hands at a distance of 4.5 feet above the ground. She measures the angle of elevation from her hand to the kite to be 20°. If the kite is 30 feet above the ground. How many feet long is the string from the kite to her hands?
What is 87.7
500
Which equation does the graph below represent?
A.) y = 3sin(1(x+0))+1
B.) y = 4sin(1(x+0))+1
C.) y = 4sin(1(x+1))+1
D.) y = 3sin(1(x+1))+1
ANSWER: A.) y = 3sin(1(x+0))+1
500
Find all the angles of this quadratic equation below.
4sec^2 θ - 36 = 0
A.) 70.5°, 250.5°, 109.47°, 289.47°
B.) 80.5°, 250.5°, 105.3°, 290.47°
C.) 80.5°, 245.5°, 115.45°, 275.47°
D.) No Solution
What is A.) 70.5°, 250.5°, 109.47°, 289.47°