Sequence and Series
Exponential Equations
Log Equations
Trig., Right angle Trig, law of sine/cosine
Trig. proofs and Trig. Equations
100
Find the next term of the sequence 2, 9, 16, 23, 30, X
695
100
Solve the equation
53-2x=5-x
x=3
100
Solve the equation
log(n+9)=log 4n
n=3
100
Two fire towers are located 10 miles apart. If each locates the same fire and finds it to be at an angle of 62 degrees and 71 degrees, respectively, from the other tower, how far is the fire from the tower nearest to it?
b=12.07 miles
100
Simplify
tan2θ X cos2θ
sin2θ
200
What is the 70th term of an arithmetic sequence whose first term is 10 and whose common difference is -4
-266
200
Solve the equation
31-2x=243
x=-2
200
solve the equation
-2log8(a+1)=-8
a=4095
200
An isosceles triangle has a base length of 20 centimeters. If the vertex angle of the triangle measures 30 degrees, find the perimeter of the triangle
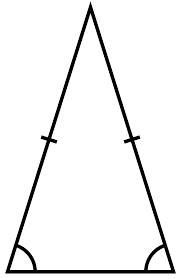
p=97.27 cm
200
simplify
Cosθ X Cscθ X Tanθ
1
300
A geometric sequence has a U2=-6 and U5=162. Find its general term.
Un=2x(-3)n-2
300
Solve the equation
(813n+2)
--------- =34
(243-n)
-4/17
300
solve the equation
log15(x2+13)=log15(-9x-1)
X=7,2
300
A jet is sighted simultaneously from two towns that are 9 miles apart. The angle of elevation of town C is 48 degrees and the angle of elevation of town D is 64 degrees. If the jet is directly above a straight line between the two towns, how far is the jet from each town?
Town D=8.7 miles
Town C= 7.213 miles
300
simplify the equation
tan2θ+ tan4θ
sec4θ-sec2θ
400
The initial population of rabbits on a farm was 50. The population increased by 7% each week.
a. How many rabbits were present after 15 weeks?
b. How long will it take for it to reach to 500?
a. 138 rabbits
b. 34 weeks
400
Solve the equation
5.1Xe10b+8-7=76.4
b=-0.5206
400
solve the equation
log3(x2+8)-log34=3
X=+ or -√10
400
Two ships sail from the same harbor at the same time on courses which diverge by 48 degrees. If the ships sail at constant speeds of 15 knots and 18 knots, how many nautical miles apart are the ships after 2 hours
a=27.399 miles
400
Simplify the equation
Cosθ+sinθ/ cosθ + cosθ-sinθ/ sinθ
cscθ X secθ
500
Ryan is a cartoonist. His comic strips have just been bought a newspaper, so he sends them the 28 comic strips he has drawn so far. Each week after the first time he mails 3 more comic strips to the newspaper.
a. Find the total number of comic strips sent after 1, 2, and 3 weeks
b. When does Ryan send his 120th comic strip?
a. 28, 31, and 34
b. 32nd week
500
Solve the equation
-2Xe9.4x-5+6= -68.9
x= 0.9173
500
Solve the eqution
log4(x2-3)+log410=1
x=+ or - √3.4
500
Mr.Keeping, Disguised as Mathman, a costumed crime fighter, is swinging back and forth in front of the window to Ms. Gibbons math class. At t=3s, he is at one end of his swing and 4m from the window. At t=7s, he is at the other end of his swing and 20m from the window.
a) What is the equation (in sine and cosine), which represents Mathman's motion
b)Find the distance of Mathman at 8, 16, and 20 seconds.
a) d=-8 sin π/4 (t-1)+12
b) t= 8 sec distance= 17.657 meters
d=-8 sin π/4 (8-1)+12
t=16 sec distance= 17.657 meters
d=-8 sin π/4 (16-1)+12
t=20 sec distance= 6.343 meters
d=-8 sin π/4 (20-1)+12
500
Simplify the equation
(2cosθ+3sinθ)2+(3cosθ-2sinθ)2
13