Angles/Eval Trig Fun
Eval Trig Fun 2
Eval Trig Fun 3
Graphing
100
Change 260˚ to radians.
(13π)/9
100
cos(-120˚)=
-1/2
100
The point (2, 7) is on the terminal side of the angle in standard position, Find
sin \theta
-(7sqrt(53))/53
100
Write an equation for a sinusoidal graph with the following properties:
A=-3, period=(2π)/3, phase=-π/4
-3sin(3(x+π/4))
200
Change
-π/8
to degrees.
-22.5˚
200
tan 330˚=
-sqrt(3)/3
200
The point (-5, 11) is on the terminal side of the angle in standard position. Find
cos \theta
-(5sqrt(146))/146
200
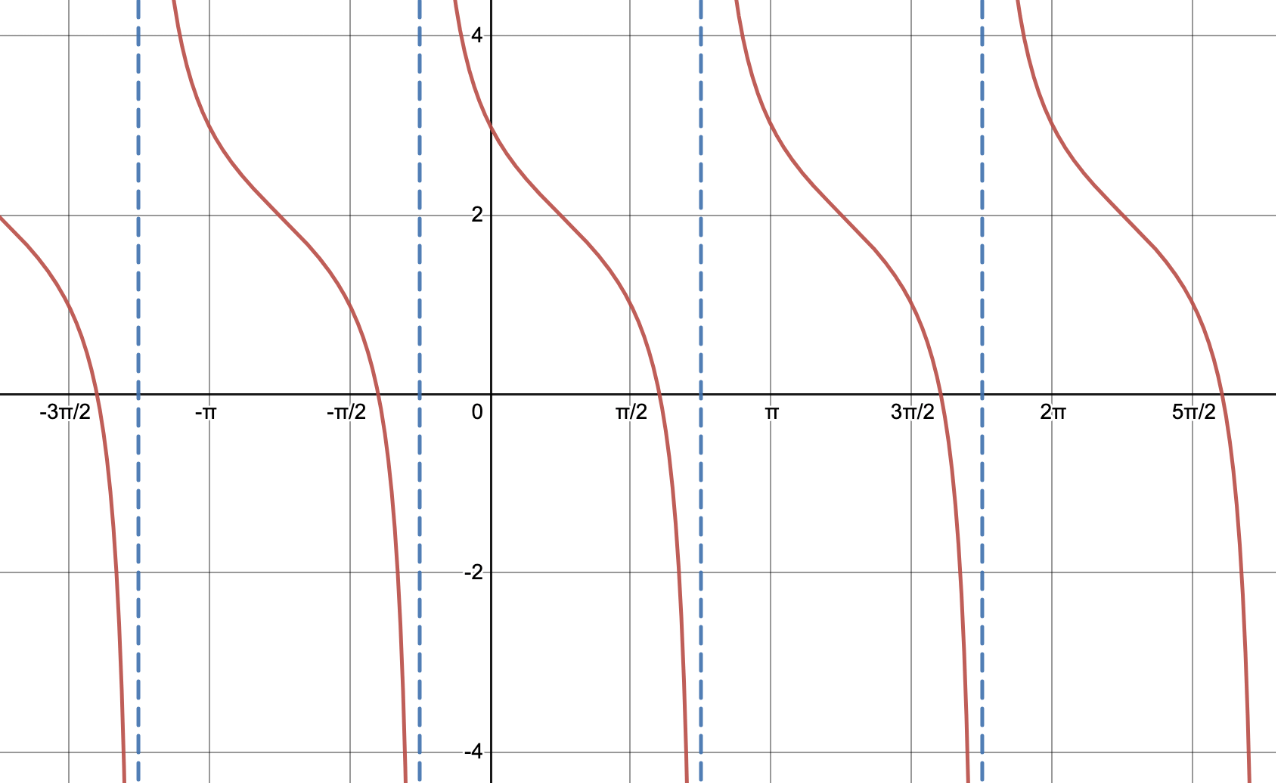
Graph
tan(-(x-π/4))+2
300
sin (π/6)=
1/2
300
sin (π/2)-tan((19π)/4)=
2
300
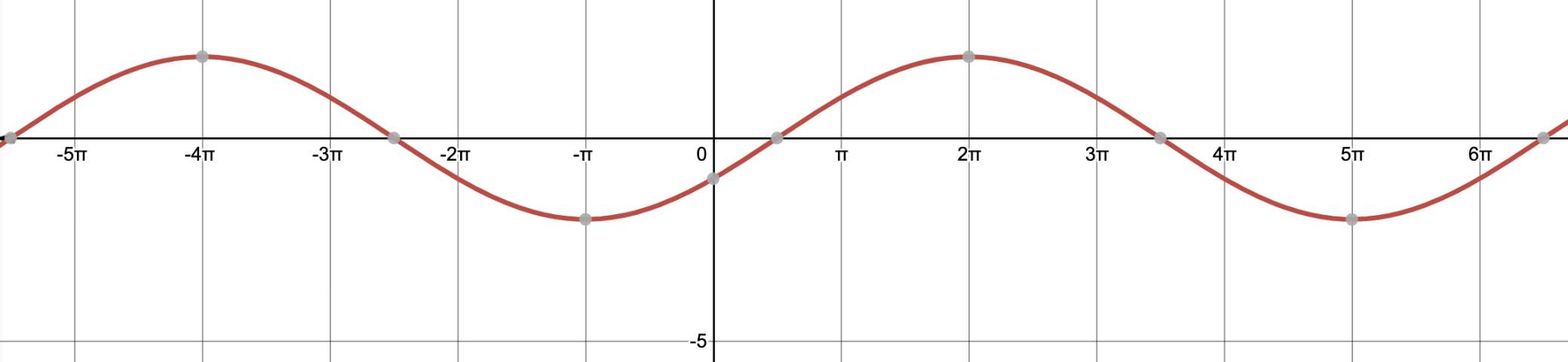
Graph
y=2sin(x/3-π/6)
400
cos(-(5π)/4)-cos((3π)/4)=
0
400
2 sin^2 60˚-3 cos 45˚=
(3-3sqrt(2))/2
500
sin \theta = 5/7, π/2 <\theta<π
find
cos \theta, tan \theta, csc \theta , sec \theta, cot \theta
cos \theta =-(2sqrt(6))/7, tan \theta=-(5sqrt(6))/12
csc\theta=7/5, sec\theta=-(7sqrt(6))/12, cot\theta=-(2sqrt(6))/5
500
If
f(x)=sin x and f(a)=3/5
find f(-a).
-3/5