The lim_(x->oo) f(x) , given the following function.
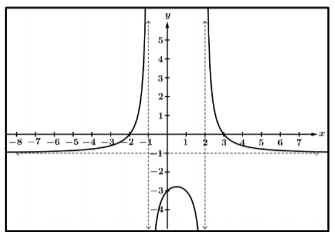
What is -1?
The intervals of this function where f(x)<=0 .
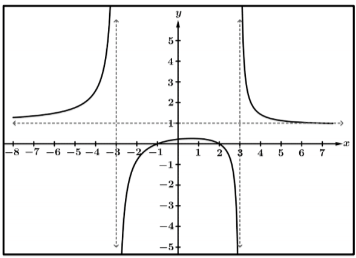
What is (-3,-1] and [2,3)?
The holes and vertical asymptotes in
k(x)=((x-1)(x+3))/((x+3)(x-2)
What is a vertical asymptote at x=2 and a hole at x=-3?
Determine if the following function has a horizontal asymptote, slant asymptote, or neither:
f(x)=(3x^3-4x+6)/(x^2-3)
What is a slant asymptote?
 Given that h(x)=-2g(x-3)-5 , the value of h(0).
Given that h(x)=-2g(x-3)-5 , the value of h(0).
What is 3?
Effective storage of the worlds busiest workers. Name this shaped storage used by bees to store honey in the most efficent way using the minimal amount of wax.
What is the honeycomb structure?
The horizontal asymptote present when the degree of the numerator is smaller than the degree of the denominator.
What is
y=0?
The intervals of this function where f(x)>=1 .

What is (-oo, -3) and (3, oo)?
The holes and vertical asymptotes in the following function:
y=((x-2)^2(x+3)(x-5)^6)/((x-2)^3(x+3)(x-5)^2)
What is a hole at x=-3 and x=5 and a vertical asymptote at x=2?
Determine if the following function has a horizontal asymptote, slant asymptote, or neither:
h(x)=(x(x-3)^2)/(3x^3-2)
What is a horizontal asymptote?

Given that g(x)=3f(x+2)-1 , the value of g(-2).
What is -2?
While Pascal's triangle is wonderful, it is actually an extension of a previous pattern. Follow a single diagonal of the triangle and you will arrive at this pattern, one where each number is the sum of the previous two.
What is the Fibonacci sequence?
The horizontal asymoptote given by the rational function r(x)=f(x)/g(x) where f(x)=2x^3+4x-1 and g(x)=6x^3-x^2+4 .
What is
1/3
Solve the following inequality: ((x-1)(x+2)^2)/(x-2)>=0 .
What is (-oo,1] and (2,oo)?
What is
h(x)=((x+4)(x-1/2))/((x+4)(x-5))=((x+4)(2x-1))/((x+4)(x-5))
Determine if the following function has a horizontal asymptote, slant asymptote, or neither:
y=((x+3)^2(2x^2-4)^2)/(x^2(x-5)(x+6)^3
What is a horizontal asymptote?

Given that h(x)=5-f(2x) , the value of h(2)
What is 3?
Nat"A mathematician confided, this strip here is one-sided. You'll get quite a laugh if you cut one in half, for it will stay in one piece when divided."
Name this mathematic shape that only has one side, which only has one side, and shares a name with a beloved Matrix character.
What is the Mobius strip?
The graph of a function that:
increases in height as the inputs decrease without bound,
decreases in height as the inputs increase without bound.
What is a graph with the following:
lim_(x->-oo)f(x)=oo; lim_(x->oo) f(x)=-oo
Solve the following inequality:
(4x-8)/(x+5)<=0.
What is (-5,-2]?
An expression for g(x) given the graph below:
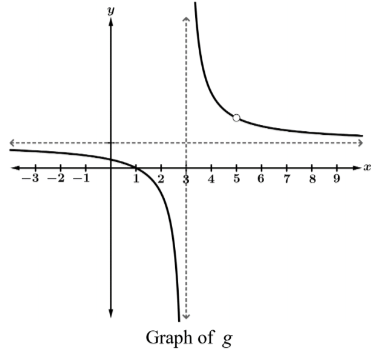
What is
((x-1)(x-5))/((x-5)(x-3)
The remainder from the following long division:
(x^3+2x^2-3x+4) divide (x-7)
What is 424?
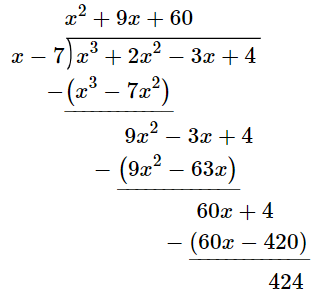
The equation of h(x) given that it is the result of applying the following three transformations to j(x): a horizontal dilation by a factor of 1/3, a vertical dilation by a factor of 2, and a vertical translation by -4 units.
What is
h(x)=2j(3x)-4?
A series of seashells spiraling in to infinity, a pattern that exists in everything from the human face, to the spines of a pinecone, to the seeds of a sunflower. Name this splended pattern, the ratio of all things that when shows a proportianl structure with a value of 1.618.
What is the golden ratio?
The limits of y as it increases and decreases without bound, given y=(4x+3)^2/((3x-1)(2x+5) .
What is y=8/3?
Solve the following inequality: (x^2-4)/(x^2-10x+25)<0 .
What is (-2,2)?
The holes and vertical asymptotes of the function r(x) given that r(x)=f(x)/g(x) , f(x)= x^3-100x , and g(x)=x^2-5x-50 .
What is a hole at x=10 and a vertical asymptote at x=-5?
The remainder from the following long division:
(3x^4-5x^2+3) divide (x+2)
What is 31?
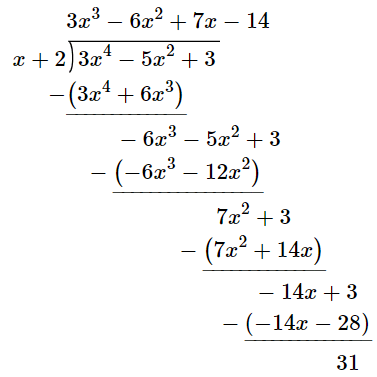
The domain and range of k(x) given that k(x)=-3f(2x)+1 and the function f(x) has the domain [-3,3] and the range [-5,3].
What is the domain [-3/2, 3/2] and range [-8,16]?
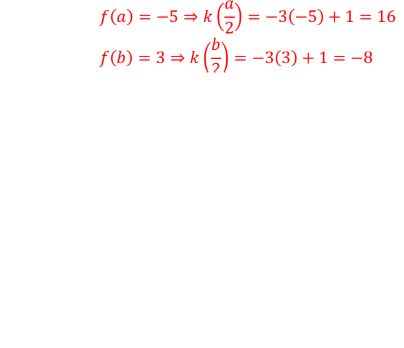
As plants grow they branch out into new buds that repeat the same shape of the original plant. These buds eventually do the same creating a pattern of repeated objects each smaller than the last. Name this pattern found in all things from tree branches, ferns, coastlines, and is even mentioned in a disney film regarding snowflakes?
What is a fractal pattern?