What is the degree and leading coefficient?
f(x)=-5x^5+3x^3-3x+1
D:5
LC:-5
Factor the polynomial:
x3+7x2+10x
x(x+5)(x+2)
What do we know about the leading term of this graph?
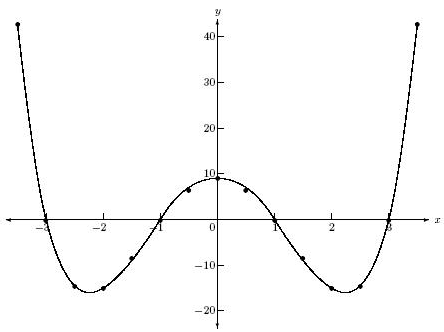
Degree: Even
L.C.: Positive
Factor the polynomial:
9x3+6x2-3x
3x(3x-1)(x+1)
Describe end behavior (using infinity)
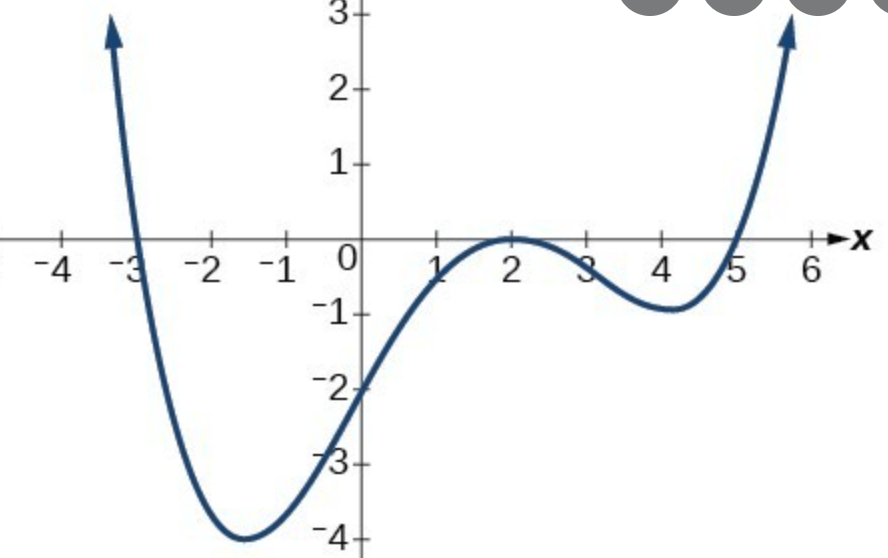
As x -∞, f(x)
∞
As x ∞, f(x)
∞
Factor the polynomial and find the zeros:
3x3+12x2-3x=12
x=-4,-1,1
Find the x and y intercepts of the function
f(x)=-2(x+1)(x-2)(x+3)
x intercepts: -1, 2, and -3
y intercept: 12
Factor the polynomial to find the zeros. You may need to use the quadratic equation.
12x3=60x2+75x
x=0, (5 +/- 5sqrt2) /2
Write a function with the following characteristics. A hole at x=3 and a HA at y=6 There are many possible answers.
What is 6x/(x-3)?
Describe the following for the graph:
Leading coefficient, degree, zeros, y intercept

L.C.: positive
Degree: even
Zeros: -3, 2, 5
Y-int: -2
Factor the polynomial to find the zeros.
x3+1=x2+x
x=-1,1
Find a function with the following characteristics. An xintercept at x= -7, a VA at x=9, a HA at y=3, and a hole at x=-2
What is 3(x+7)(x+2)/(x-9)(x+2)?