convert 135o to radians. Give your answer in terms of pi
(3pi)/4
The point (-4/5, -3/5) lies on the unit circle. Find the value of secx
secx = 1/cosx = 1/(x value on unit circle) = -5/4 or -1.25
Period of sinx
2pi
range of y = 4sin(x - 90o)
-4<=y<=4
In which quadrants is cosecant (csc) positive?
Quadrant 1 and Quadrant 2 (same place sin is positive)
Angle of
(16pi)/3
Find a coterminal angle between 0 and
2pi
(4pi)/3
a. sin21 = a/13 --> 4.7
b. cos21 = b/13 --> 12.1
Range of secx
y <=-1 uu y >=1
give three asymptotes of y = cot(x/2)
... ,-4pi, -2pi, 0, 2pi, 4pi, 6pi, ...
Which quadrant has cosx < 0 and cotx > 0?
Quadrant 3
Find the reference angle for
(16pi)/3
pi/3
The angle of elevation to the top of a building from a point on the ground 30 yards from its base is 37°. Find the height of the building to the nearest yard.
tan37 = x/30 --> x = 22.607 = 23 yards
Asymptotes between -2pi and 2pi for tanx
-3pi/2, -pi/2, pi/2, 3pi/2
Range of y = 5tan(3x - pi/6) + 4
All real numbers
If cos u = 1/3 and tan u < 0, find the value of u in degrees. Round to two decimal places
cos-1(1/3) = 70.53o but tan < 0 so should be in quadrant 4.
reference angle 70.53o
actual angle u = 360 - 70.53 = 289.47o
Find the arc length: Circle with radius of 20 feet. Central angle of 75o. Round to two decimal places if needed.
1. convert 75o to radians
2. s =
r*theta = (5pi)/12 * 20
Answer: 26.18 feet
A 73-foot rope from the top of a circus tent pole is anchored to the flat ground 43 feet from the bottom of the pole. Find the angle, to the nearest tenth of a degree, that the rope makes with the pole.
in your drawing, looking for the top angle not the bottom angle.
sinx = 43/73 --> sin-1(43/73) = x --> x = 36.1o
What's the difference between tanx and cotx graphs?
tanx goes up, cotx goes down.
tanx goes through (0,0). cotx has an asymptote at x = 0
Write a sin equation for the graph below
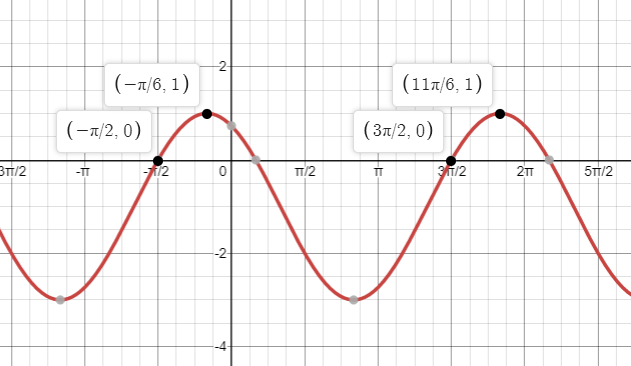
y = -2sin(x-pi/3)-1
If cotx = -3 and sinx > 0, then secx = ?. Round to two decimal places
cotx < 0 and sinx>0 means x is in quadrant 2 and secx < 0
cotx = -3 --> tanx = -1/3 --> tan-1(-1/3) =-18.43o
Reference angle = 18.43.
sec(18.43) 1/cos(18.43) = 1.05 but said in quadrant 2, secx is negative
final answer: - 1.05
If (-2, 5) is a point on the terminal side of angle u, find the exact value of csc(u).
radius =
sqrt(29)
csc(u) =
1/sin(u)
=
sqrt(29)/5
What's the difference between secx and cscx graphs?
cscx has an asymptote at x = 0.
secx has a y-intercept at x = 0 (y = 1)
Write a sec equation for the graph below
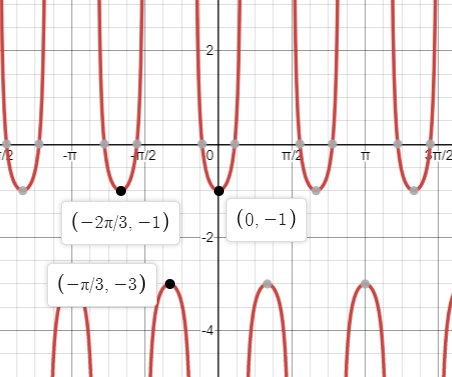
y = sec(3x) - 2