The slope m, between two points (x1,y1) and (x2,y2).
What is m=
(y_2 -y_1)/(x_2-x_1
Do these ordered pairs represent a function?
{(-3,7),(2,6),(1,9),(4,6)}
Yes, each input value has exactly one output value.
Find the domain of f(x)=(x+3)3 -6
All real numbers
(-oo,oo)
True of false
The domain of a function, [3,7) includes the point at x=7.
False
What kind of transformation does f(x+5) represent?
Point Slope form of a line
y-y1=m(x-x1)
Does the equation represent y as a function?
x=-y+5
Yes, the equation is a function.
Find the domain of
f(x)=root(x)
using the graph 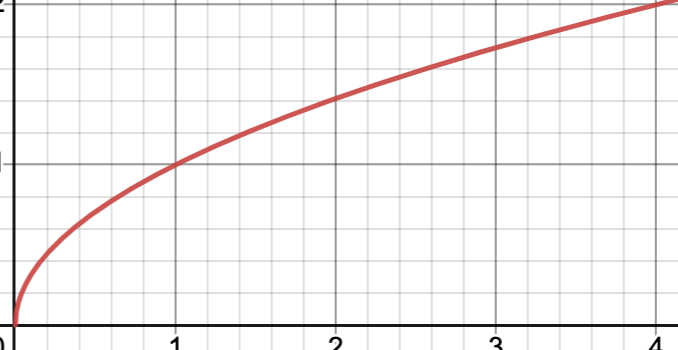
[0,oo)
or x>=0
Graphically, we test for functions by using the
The vertical line test
What is the parent graph of this function?
g(x)= 5 sqrt(x-3) -1
f(x)= sqrt(x)
Write the equation of a line that passes through the point (-5,4) and has a slope of m=2
y=2x+14
Evaluate
q(t)=(2t^2+3)/(t^2)
at t=3
g(3)=7/3
Find the domain of
g(x)=root3(x-4)
All real numbers
(-oo,oo)
Is this function even, odd, or neither?
f(x)=x^3-2x^2+5
Neither
Graph f(x) = (x+2)3 and describe its transformation from its parent graph.
Left 2 units
Determine the slope and y-intercept (if possible) of
2x-5y+10=0
m=-2/5 b=-2
Evaluate the function
g(x)=x^2 -8x +3 at g(x+5)
x^2 +2x-12
Find the domain of
h(x)=1/x - 3/(x+2)
x!= 0,-2
(-oo,-2)U(-2,0)U(0,oo)
Is this function even, odd, or neither?
Even
Describe the transformation that happens from
f(x) =x2 and h(x)= -(x2) +4
A reflection across the x-axis and then a vertical shift up 4
Write the equation of a line that is parallel to 3x-2y=6 and passes through the point (1,-4).
y= -2/3x-10/3
Find the difference quotient
[f(x+h)-f(x)]/h
of
f(x)=2x^2-x
2h+4x-1
Find the domain of
z(x)=sqrt( x-4) /(2x-6)
x>=4
[4,oo)
Graph the function and then estimate the relative minimum or maximum.
f(x)=x^2-4x-5
Relative minimum (2,-9)
Graph f(x)=|x| and g(x) = -|x-4|-7