Vocab
Quadratic Functions & Polynomial Functions of a higher Degree
Real Zeros of Polynomial Functions & Complex Numbers
The Fundamental Theorem of Algebra & Rational Functions and Asymptotes & Graphs of Rational Functions
100
Degree of a Polynomial Function
The highest variable power, n, for any function of the form f(x)=a_n x^n+a_(n-1) x^(n-1)+⋯+a_2 x^2+a_1 x+a_0
100
Describe how the graph
y=-(x-4)^2+1
is related to
y=x^2
.
Opens in the opposite direction
Translated left 4 units
Translated down 1 unit
RAX
L4
D1
100
Divide using long division.
(24x^2-x-8)/(3x-2)
8x+5+2/(3x-2)
100
Find all the zeros of the function, write the polynomial as a product of linear factors, use your factorization to determine the x-intercepts of the graph of the function.
f(x)=x^3-5x^2-7x+51
x=-3,4+-i
(x+3)(x-4-i)(x-4+i)
(-3,0)
200
Vertex Form of Quadratic
f(x)=a(x-h)^2+k
Where (h,k) is the vertex of the parabola.
200
Describe the graph of the function and identify the vertex and any x-intercepts.
f(x)=(x-4)^2-4
Parabola that opens upward
Vertex: (4,-4)
x-int: (2,0), (6,0)
200
Use synthetic division.
(2x^3+6x^2-14x+9)/(x-1)
2x^2+8x-6+3/(x-1)
200
Write a polynomial function in expanded form with real coefficients that has the given zeros: 2, -2, 2i (There are many correct answers)
f(x)=x^4-16
300
Upper/Lower Bound Test
If dividing a polynomial by a linear divisor (x - c) with synthetic division, check the result.
If c is positive and everything is either positive or zero, c is an upper bound.
If c is negative and everything alternates in sign from positive to negative, c is a lower bound.
300
Write the vertex form of the quadratic function that has the vertex (2,3) and passes through the point (0,2).
f(x)=-1/4(x-2)^2+3
300
Evaluate using the remainder theorem at f(-2).
f(x)=x^4+10x^3-24x^2+20x+44
-156
300
Find the domain of the function and any asymptotes.
(2-x)/(x+3)
Domain: All real numbers x except x=-3
V.A. x=-3
H.A. y=-1
400
Rational Function
f(x)=(N(x))/(D(x) )
Where N(x) and D(x) are polynomial functions
400
Describe the transformation of the function from f(x)=x3.
f(x)=-(x-1)^3+3
Rises to the left, Falls to the right
Right 1 unit
Up 3 units
400
Verify that the factor (x-4) is a factor of
f(x)=x^3+4x^2-25x-28
. Find the remaining factors. List all the real zeros.
(x+1)(x+7)
x=4, -1, 7
400
Find the domain of the function and any asymptotes.
2/(x^2-3x-18)
Domain: All real numbers x except x = 6, -3
V.A. x=-3, x=6
H.A. y=0
500
Vertical Asymptote
The vertical line x=a of the graph of f when f(x)→∞ or f(x)→-∞ as x→a , either from the right or from the left.
500
Use the Leading Coefficient Test to describe the end behaviors of the graph.
-x^5-7x^2+10x
Up to the left, Down to the right
500
Use the Rational Zero Test and list all the possible rational zeros.
f(x)=10x^3+21x^2-x-6
+-1,+-2,+-3,+-6,+-1/10,+-1/5,+-3/10,+-2/5,+-1/2,+-3/5,+-6/5,+-3/2
500
Find the domain of the function and any asymptotes.
(7+x)/(7-x)
Domain: All real numbers x except x=7
V.A. x=7
H.A. y=-1
600
Horizontal Asymptote
The line y=b of the graph f when f(x)→b as x→∞ or x→-∞.
600
Find the zeros and their multiplicities algebraically approximate any zeros using a graphing utility.
f(x)=x(x+3)^2
x=-3, -3, 0
600
Use Descartes’s Rule of Signs to determine the possible number of positive and negative real zeros.
3 or 1 positive real zero
0 negative real zeros
600
Find all asymptotes and holes of the graph:
f(x)=(2x^2-7x+3)/(2x^2-3x-9)
V.A.: x=-3/2
H.A.: y=1
Hole: (3, 5/9)
700
Intermediate Value Theorem
If (a,f(a)) and (b,f(b)) where f(a)nef(b) , then for any number d between f(a) and f(b) there must be a number c between a and b such that f(c)=d
700
Write a polynomial function that has the given zeros. (there are several possible answers)
-2, 1, 1, 5
f(x)=a(x+2)(x-1)^2(x-5)
700
Solve and write the result in standard form.
sqrt(-9)+3+sqrt(-36)
3+9i
700
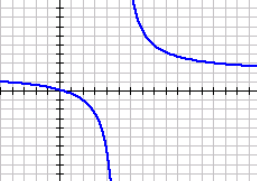
Sketch the function
f(x)=(2x-1)/(x-5)
800
Linear Factorization Theorem
If f(x) is a polynomial of degree n , where n>0 , then f has precisely n linear factors f(x)=a_n (x-c_1 )(x-c_2 )⋯(x-c_n ) where c_1,c_2,⋯,c_n are complex numbers.
*Note: This also means that f MUST have n complex roots.*
800
Use the Intermediate Value Theorem and a graphing utility to find approximate a zeros of the function
f(x)=2x^4+7/2x^3-2
Intervals/Approximations
(-2,-1), (0,1)
x=-1.897, 0.738
800
Write the quotient in standard form.
(1-7i)/(2+3i)
-19/13-17/13i
800
True or False: The Upper/Lower Bound test can only tell you if negative numbers are Lower Bounds for the zeros of a polynomial and positive numbers can be Upper Bounds for the zeros of a polynomial.
C. True!