Transformations
Inverses
Properties
Relations
Compositions
100
What is an equation for the squaring function shifted up by 2?
f(x) = x2 + 2
100
What is an equation for the inverse of the function f(x) = 5x, if the inverse exists?
f(x) = x/5
100
What is the vertical and horizontal asymptotes for
f(x)=(2x-7)/(6-x)
x = 6
y = -2
100
Find the (x,y) pair for the value of the parameter t = 2
x=t and y=t^2/4
(2,1)
100
What is the equation for f(g(x))?
f(x) = x^2 and g(x) = x – 2
f(g(x)) = (x – 2)^2
200
What is an equation for the absolute value function shifted to the left by 20?
f(x) = |x + 20|
200
What is the equation for the inverse of the function f(x) = 7x + 1, if the inverse exists?
f(x) = (x – 1)/7
200
What is the domain?
f(x)=(7x)/[(x-3)(x+2)]
(-oo,-2)uu(-2,3)uu(3,oo)
200
Find the (x,y) pair for the value of the parameter t = -3
x=-2t and y=t^2-5
(6,4)
200
What is the answer for g(f(5))?
f(x)=4x-3 and g(x)=x-2
g(f(5)) = 15
300
What is an equation for the cubic function stretched vertically by a factor of 4 and reflected across the y-axis?
f(x) = 4(-x)3
300
What is the equation for the inverse of the function, if the inverse exists?
f(x) = x/2 + 15
f(x) = 2(x – 15)
300
What is the absolute maximum and the absolute minimum?
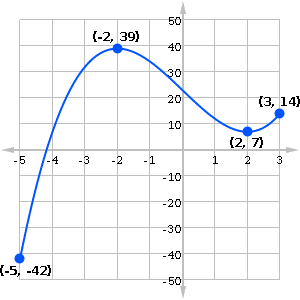
Absolute maximum at y = 39 ; absolute minimum at y = -42
300
Find the (x,y) pair for the value of the parameter t = -1 and t = 3
x=-2t-3 and y=2t^2+2t-5
(-1,-5) and (-9,19)
300
What is the equation for f(g(x)) and g(f(x))?
f(x)=-2x^2 and g(x)=3x+4
f(g(x))=-18x^2-48x-32
g(f(x))=-6x^2+4
400
What is an equation for the quadratic function shifted up by 5, to the right by 4, and reflected across the x-axis?
f(x) = – (x – 4)2 + 5
400
What is the equation for the inverse of the function, if the inverse exists?
f(x)=(3x-1)/(x+2)
f^(-1)(x)=(2x+1)/(3-x)
400
Indicate the intervals where the graph is increasing, decreasing, and constant.
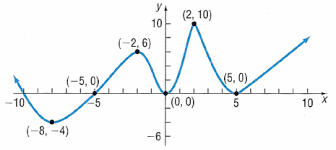
Increasing:
(-8,-2),(0,2),(5,oo)
Decreasing:
(-oo,-8),(-2,0),(2,5)
Constant: none
400
Find the relationship between x and y algebraically.
x=t+3 and y=t^2-2
y=x^2-6x+7
400
What is the answer for f(f(2)) and g(g(3))?
f(x)=6x+2 and g(x)=x-5
f(f(2)) = 86
g(g(3)) = -7
500
A function, f(x)=-4(x+3)2-5, is shifted up by 3 and translated left 2 units. What is the equation of the new function?
f(x) = -4(x+5)2-2
500
What is the test to determine if a relation's inverse is a function?
How do you verify 2 functions are inverses of each other algebraically?
Horizontal Line Test
F and G are inverses if f(g(x))=x and g(f(x))=x
500
Is the following function bounded above, below, or both? Then give the range.
f(x)=2-(x+3)^2
Bounded above
(-oo,2]
500
Find the (x,y) pair for the value of the parameter t = -3. Then find the relationship between x and y algebraically.
x=(t+3)/2 and y=2t^2-1
(0,17)
y=8x^2-24x+17
500
What is the equation for h(g(f(x)))?
f(x)=2x^2-x, g(x)=x-5, and h(x)=x/3
h(g(f(x))) = (2x^2 – x – 5)/3