Degrees, Radians and DMS
Trig Functions of Acute Angles
Circular Functions
Arc length and area of a sector
Problem Solving
100
Convert 3pi/7 to degrees. Round to the nearest hundredth of a degree.
77.1 degrees.
100
For an acute angle, A, in a right triangle, the ratio of the length of the opposite leg to the length of the hypotenuse.
sinA
100
Two angles are ___________ if they have the same initial side and terminal side, but have different measures.
Coterminal
100
What is the arc length formula for a sector?
S=theta * r
100
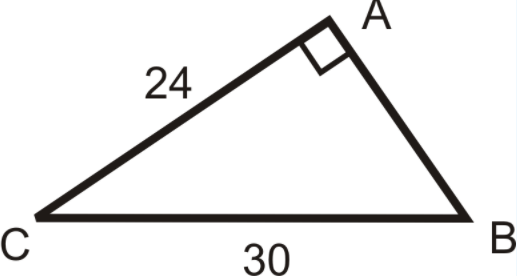Find the length of AB
18
200
Convert 24 degrees into radians. Reduce your answer to the simplest fraction.
2pi/15
200
Find cosA and tanA if sinA = 5/13.
cosA = 12/13; tanA = 5/12.
200
Find one positive and one negative angle that are coterminal with -142 degrees.
+218 degrees; -502 degrees (other coterminal angles acceptable, also)
200
What is the area of a sector formula?
A= 1/2 * theat * r^2
200
Find the measure of angle B.
50o
300
Convert 150.625o into Degree-Minute-Second Form
150o 37' 30"
300
Using the unit circle, evaluate sec(pi/3).
2
300
Find sine trig of angle A, whose terminal side contains the point (-8,15).
sinA = 15/17
300
Use the arc length formula to find the arc length if the radius is 5ft and the central angle measures 18 degrees.
pi/2 ft
300
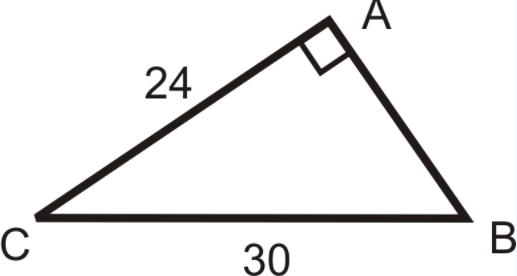Find the measure of angle B
approximately 53.13 degrees
400
Convert 118.32 from decimal form to DMS.
118 degrees, 19 mins, 12 sec
400
Find cotA if the measure of angle A is 135 degrees (use your unit circle!)
-1
400
Find the 6 trig functions of 330 degrees.
sin(330) = -1/2; cos(330) = sqrt3/2; tan(330) = -1/sqrt3
csc(330) = -2; sec(330) = 2/sqrt3; tan(330) = -sqrt3
400
How far has the hour hand (which has a length of 6 inches) traveled if it goes from 12:00 - 4:00 on a clock? Round to the nearest tenth.
12.6 inches
400
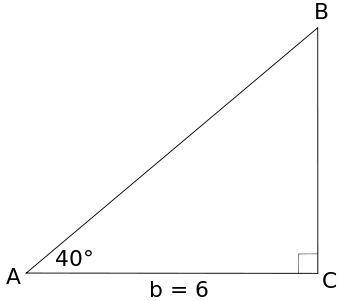
Find the measure of side BC
approximately 5.035
500
Convert 48 degrees, 30 mins, 36 sec from DMS to degrees.
48.51 degrees
500
A guy wire from the top of a transmission tower forms a 75 degree angle with the ground at a 55 ft distance from the base of the tower. How tall is the tower?
205.26 ft.
500
Find secA and cscA if cotA = -4/3 and cosA < 0
secA = -5/4; cscA = 5/3
500
What is the area of the region formed between the hour and minute hand if it is 4:00 on a clock with a radius of 6 inches? (Hint: Draw a picture to help you!)
37.7 in2
500
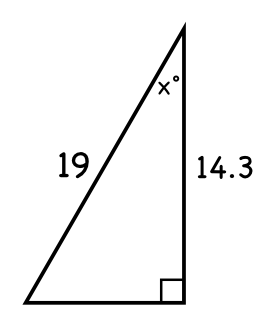
Find the value of x and the missing side length
x=41.181 degrees
Missing side = 12.510