Find the zero of the linear function.
f(x) = -4x+7
x = 7/4
Determine whether the relation represents a function
{(-1,8), (2,4), (4,-5), (8,-2)}
What is yes
What is a function
Solve and write interval notation for the solution set. Then graph the solution set.
-2</=x+5</= 4
Find the slope of the line containing the points
(−10,−4)
and
(−10,4).
The slope is undefined.
Solve:
29 - (2/7)x = -(2/7)x + 29
All real numbers
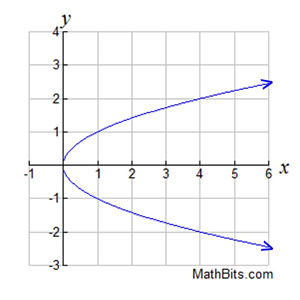 Is this a function?
Is this a function?
What is no
A person buys a phone for
$85 and signs up for a single-line phone plan with 2000 monthly anytime minutes. The plan costs $119.98 per month. Write an equation that can be used to determine the total cost, C(t), of this phone plan for t months. Then, find the cost for
21 months, assuming that the number of minutes the person uses does not exceed 2000 per month.
C(t) = 85 + 119.98t
C(21) = 2604.58
Determine whether (7, 4) is a solution to the equation y = 18x + 8
No
Determine whether the relation is a function. Identify the domain and the range.
{(3,15), (6,30), (7,35)}
Yes
Domain: {3, 6, 7}
Range: {15, 30, 35}
The perimeter of a rectangular field is
320yd. The length is
80yd longer than the width. Find the dimensions.
40 and 120
Given that g(x)=2x^(2)−2x+4,
find each of the following.
g(1−t)
g(1−t)=2t^(2)−2t+4
Juliet has a choice between receiving a monthly salary of $1360 from a company or a base salary of $1200 and a 4% commission on the amount of furniture she sells during the month. For what amount of sales will the two choices be equal?
$4000
Find the domain of the function.
f(x) = (x+7)/(-1+x)
Give answer in interval notation
(-inf, -1) U (-1, inf)
The annual per-capita consumption of whole milk in country A was
27.1gal in 1980. By 2011, this amount had decreased to 6.2 gal. Find the average rate of change in per-capita consumption of whole milk from 1980 to 2011.
Decrease of .7 gal per year.
Find f(a+1) for f(x)=2(x-1)2+3
What is 2a2+3a+3
(7/9) - 5x = -5x + (1/9)
No solution
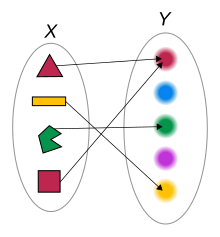 Is this a function?
Is this a function?
What is no.
Suppose that for some function g,
g(x+3) = 4x+2.
Find
g(−2).
g(-2) = -18