Quadratics
Graphing Polynomials
Synthetic Division
Rational: vertical asymptote
Rational: horizontal asymptote
100
What equation do we use to find the x-value for the max/min of a quadratic?
What is
x=-b/(2a)
100
How do you find the degree of a polynomial in factored form?
What is. . .
count all the factors (binomials). If there are multiplicities, add up the multiplicities to get the degree.
100
How do we know that a factor is a root of a polynomial using synthetic division?
What is. . .
we get a remainder of zero
100
Find all vertical asymptotes of:
r(x)=4/(x-2)
What is
x=2?
100
What is the horizontal asymptote of the following rational:
r(x)=(3x^2+2)/(4x^2-7)
What is y=3/4 ?
200
What does
f(-b/(2a))
give you in a quadratic?
What is the value of the max/min?
200
Consider the polynomial:
p(x)=-(x)^3(x-3)
What is the end behavior?
What is. . .
Down and down (negative, even)?
200
Let's say we check to see if x=1 is a root of
x^7+x^2+10
.
What will be the degree of the "reduced" polynomial after going through synthetic division?
What is. . .
6.
200
Find all vertical asymptotes of
r(x)=(4(x-2))/((x-2)(x+3))?
What is x=-3?
200
What is the horizontal asymptote of the following rational:
r(x)=(3x^2+2)/(4x^3-7)
What is y=0 ?
300
A fountain sprays water in an arc, and the height of the water above the ground, as a function of time can be represented by
h(t)=-0.5t^2+3t+1
.
How do we find the max height that the water gets to?
What is plug in t=-b/(2a) into h(t)?
300
Consider the factor:
(2x-3)^6
.
What is the root and how does the polynomial hit this root?
What is. . .
x=3/2
Bounce.
300
Say we test x=1 into a quadratic using synthetic division, and end up with the following "last line":
1 3 |0.
What are the two roots of this quadratic?
What is
x=1, and x=-3?
300
Find all vertical asymptotes of
r(x)=((x-2)(x+3)(x-7))/x^2
What is
x=0?
300
What is the horizontal asymptote of the following rational:
r(x)=(3x^3+2x^6+10)/(4x^3-10x^2+7)
What is. . .
there is none!
400
A fountain sprays water in an arc, and the height of the water above the ground, as a function of time can be represented by
h(t)=-0.5t^2+3t+1
.
The roots of this function are at t=-0.32 and t=6.32.
What do EACH of these values mean in CONTEXT?
What is. . .
t=-0.32 has NO meaning in this context
t=6.32 is the time at which the water hits the ground.
400
Consider the polynomial:
p(x)=-x^101
As
x to +\infty, p(x) to ?
What is. . .
- infty ?
400
How can we set up synthetic division to prove the following:
x^7-4x^5-3x^3+6x^2+2x-4=(x-2)(x^6+2x^5-3x^2+2)
Place x=2 into synthetic division with the coefficients 1,-4,-3,6,2,-4.
We should end up with the coefficients 1, 2, -3, 2
400
Looking at a graph of rational function, how do you identify the vertical asymptotes?
Look at the dotted vertical lines at which the graph approaches
\pm \infty
400
Looking at a graph of rational function, how do you identify the horizontal asymptote?
What is. . .
look at the horizontal line that the graph approaches on either ends (as
x to \pm \infty
500
Consider the following profit function
P(x)=-5(x-50)^2
where
P(x): profit
x: units produced and sold
In this example, the vertex (maximum) is equal to its single root at x=50.
Explain what this means in context?
What is. . .
this is the point when the business "breaks even", the point when they don't make or lose money. Selling more or fewer units results in a loss, so the only point where they break even is at exactly 50 units.
500
A polynomial is a CONTINUOUS graph. This means there are no breaks in the graph.
Is it possible for a polynomial to have 8 bumps and no x-intercepts?
What is. . .
YES! Think of an even degree polynomial with only complex roots.
500
Rational root theorem:
What are all the possible
p/q
for the following polynomial:
p(x)=2x^5+4x^4-3x^3+2x^2-x+12
What is. . .
p/q=\pm 1/2, 1, 3/2, 2,3,4,6,12
500
Describe the end behavior near the vertical asymptote at
x=4
:
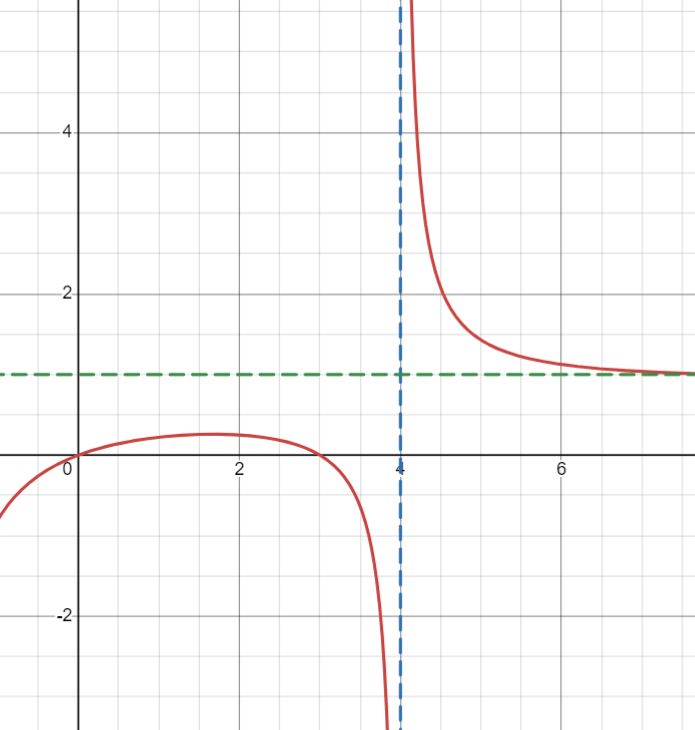
What is. . .
as
x to 4^+, r(x) to +\infty
x to 4^-, r(x) to -\infty
500
Describe the end behavior near the horizontal asymptote:
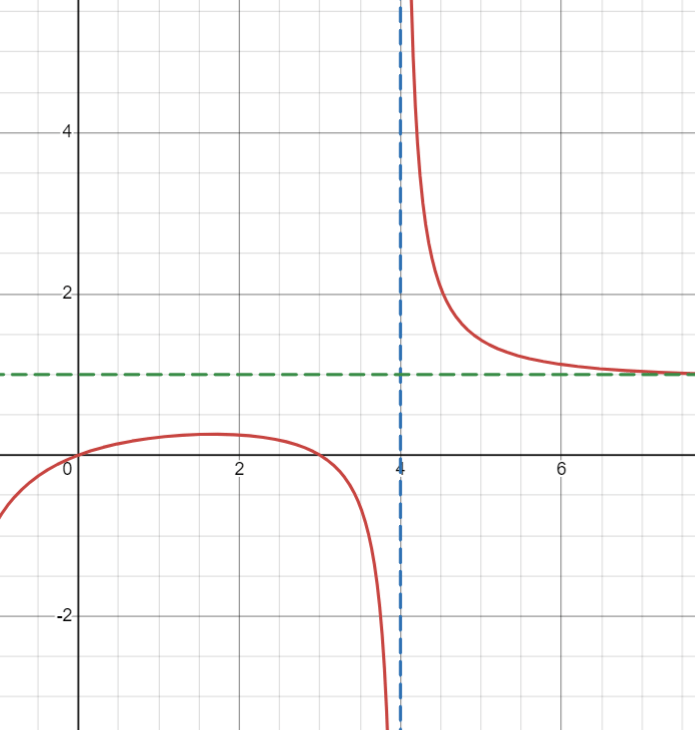
What is
as x\to +\infty, r(x)\to 1