classical
empirical
axiomatic
Random
100
a witch flips a coin. what are the chances that it's heads?
what is 1/2
100
Based on the experiment, what was the probability of getting a tails?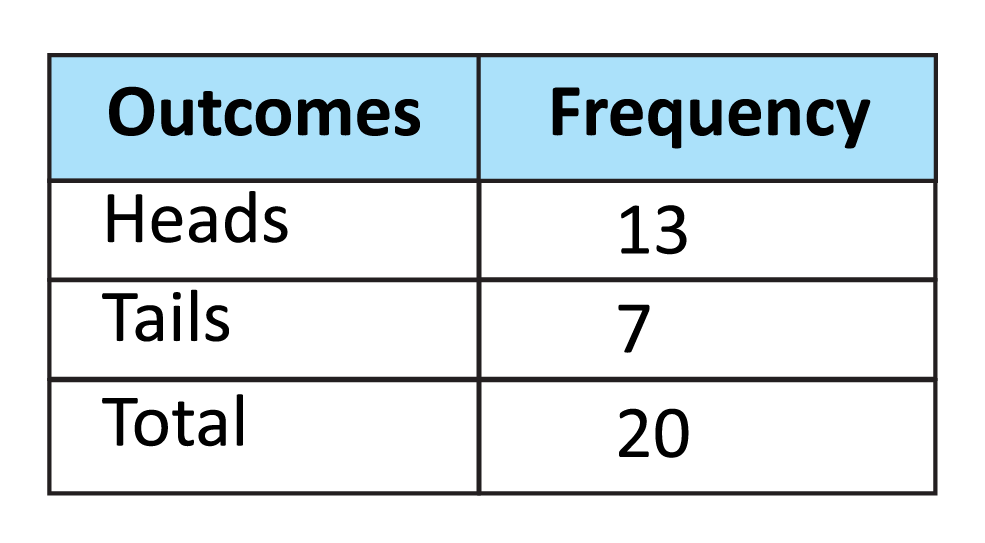
7/20
100
is drawing a card that is simultaneously a red card and a club mutually exclusive?
yes
100
a trick or treater has just lost their costume in their room. if they have 3 drawers with equal amounts of clothing in each drawer, what is the probability of their costume being in the first drawer they look in?
1/3
200
A ghost rolls a fair die. What are the chances that it lands on a 2?
what is "1/6"
200
Based on this experiment, what was the probability of getting heads?
13/20
200
the probability of flipping a coin and getting heads three times in a row
If you flip a coin, the chances of you getting heads is 1/2. This is true every time you flip the coin so if you flip it 3 times, the chances of you getting heads every time is 1/2 * 1/2 * 1/2, or 1/8.
200
If three coins are tossed simultaneously, then the probability of getting at least two heads, is
1/2
300
a pumpkin, a squash, a Cucurbita maxima, and a gourd are having a tea party. They each brought a gift and laid them down on a table. They then pick up a random gift and open it. what are the chances of the gourd opening up its own gift?
what is "1/4"
300
Based on the information shown, what is the probability of selecting an enlisted marine out of all marines?
8928/9782
300
In an election, there are four candidates. Let the four candidates be A, B, C, and D. Based on the polling analysis, it is estimated that A has a 20 per cent chance of winning the election this time, while candidate B has a 40 per cent chance of winning the election. What is the probability that candidate A or B will win the election?
Solution) We notice that the events that {A wins election}, {B wins election}, {C wins election}, and {D wins election} are disjoint events since more than one of the events cannot occur at the same time. For example, if candidate A wins, then candidate B cannot win the elections. We know that the third axiom of probability states that,
If A and B are mutually exclusive outcomes, then P (A1 ∪ A2) = P (A1) + P (A2).
Therefore, Probability P (A wins election or B wins election) = P ({A wins the election} ∪ {B wins the election}) = P ({A wins election}) +P ({B wins election})
=P ({A wins election}) +P ({B wins election})
=(20/100)+(40/100)
=0.2+0.4
= 0.6
300
A card is drawn from the set of 52 cards. Find the probability of getting a queen card.
1/13
400
You are blindfolded and spun around ten times. You are asked to touch a rectangular candy corn with each of its colors taking up equal areas. What are the chances you touch the yellow section?
what is "1/3"
400
based on the informational shown above, what are the chances of selecting a marine out of all the soldiers?
9782/198420
400
2. Three coins are tossed up in the air, one at a time. What is the probability that two of them will land heads up and one will land tails up?
- 0
- 1/8
- 1/4
- 3/8
D
400
What is the probability that a number selected from the numbers (1, 2, 3,..........,15) is a multiple of 4?
1/5
500
there are 30 pieces of candy in a jar. If there are 6 pieces of snickers, twix, twizzlers, dum dums, and sour patch kids, what are the chances a trick-or-treater will get a snickers?
What is "1/5"
500
Based on the information shown below, what is the probability of selecting an Army officer at random?
10367/198420
500
8. An MP3 player is set to play songs at random from the fifteen songs it contains in memory. Any song can be played at any time, even if it is repeated. There are 5 songs by Band A, 3 songs by Band B, 2 by Band C, and 5 by Band D. If the player has just played two songs in a row by Band D, what is the probability that the next song will also be by Band D?
The probability of playing a song by a particular band is proportional to the number of songs by that band divided by the total number of songs, or 5/15=1/3 for B and D. The probability of playing any particular song is not affected by what has been played previously, since the choice is random and songs may be repeated.
500
100 cards are numbered from 1 to 100. Find the probability of getting a prime number.
1/4