Simple Probability
Theoretical Probability
Experimental Probability
Marbles/Determine Probability
Probability Models
100
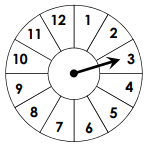
P(even number) =
6/12 = 1/2 = 0.5 = 50%
100
There are 2 blue, 6 yellow, 10 red, 3 green, 5 orange, and 4 purple marbles in a jar. One marble is chosen at random.
P(red or blue)=
12/30 = 2/5 = 0.4 = 40%
100
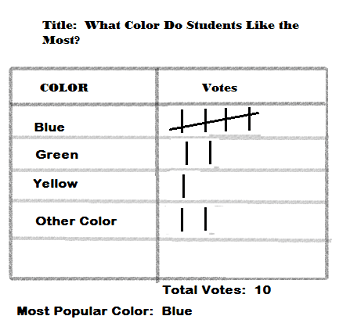
What is the experimental probability of choosing green based on the data?
2/10 = 1/5 = 0.2 = 20%
100
Randomly select a colored marble from a bag that contains 5 red marbles, 5 blue marbles, 5 green marbles, 5 yellow marbles, and 5 purple marbles.
What is my sample space?
{R, B, G, Y, P}
100
Randomly select a coin from a jar that contains 14 quarters, 26 dimes, 12 nickels, and 8 pennies.
Draw the probability model.
200
P(not a triangle)=
6/8 = 3/4 = 0.75 = 75%
200
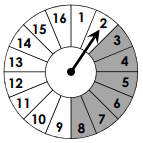
P(grey)=
6/16 = 3/8 = 0.375 = 37.5%
200
What is the experimental probability of choosing grapes based on the data?
round to the nearest percent
6/19 = 0.32 = 32%
200
Randomly select a colored marble from a bag that contains 5 red marbles, 5 blue marbles, 5 green marbles, 5 yellow marbles, and 5 purple marbles.
What is P(G)?
1/5
200
What is always the sum of every probability model?
1 whole or 100%
300
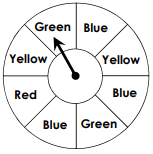
P(green or blue)=
5/8 = 0.625 = 62.5%
300
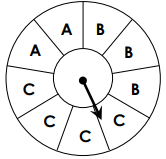
P(C)=
4/9 = 0.444444 = 44%
300
A piece of fruit was selected from a basket 40 times. The results are shown in the table below.
What is the experimental probability of choosing a banana or a cherry?
12/40 = 3/10 = 0.3 = 30%
300
Randomly select a colored marble from a bag that contains 5 red marbles, 5 blue marbles, 5 green marbles, 5 yellow marbles, and 5 purple marbles.
Are the probabilities equally likely?
Yes, because every color of the marbles has the same chance of being selected.
300
How can we tell when a probability model is uniform?
When all of the probabilities have the same chances of occurring.
400
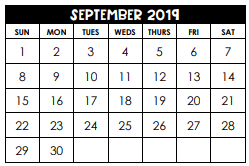
P(a date that is a multiple of 5)=
6/30 = 1/5 = 0.2 = 20%
400
Cara is playing a number game where she has two tiles for each number 0 – 9.
P(a number less than 3)=
6/20 = 3/10 =0.3 = 30%
400
A marble is picked from a jar 60 times. Results are shown in the table below.
What is the experimental probability of not choosing a black marble?
48/60 = 4/5 = 0.8 = 80%
400
Determine the probability of the event.
A coin is flipped and the coin lands heads up. Express the probability as a fraction.
1/2
400
Randomly select a coin from a jar that contains 14 quarters, 26 dimes, 12 nickels, and 8 pennies.
What is P(Dimes)?
26/60 = 13/30
500
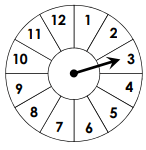
P(prime number)=
(round to the nearest percent)
5/12 = 0.42 = 42%
500
P(grey)=
(round to the nearest percent)
12/36 = 1/3 = 0.33 = 33%
500
A number between 1 and 3 is chosen at random 30 times.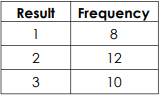
What is the experimental probability of choosing a 1? What would be the theoretical probability of choosing a 1?
Round to the nearest percent.
Experimental: 8/30 = 4/15 = 0.27 = 27%
Theoretical: 10/30 = 1/3 = .33 = 33%
500
Determine the probability of the event.
You have only white shirts in your closet. Express the probability of reaching into your closet and choosing a red shirt as a fraction.
0/100
500
Randomly select a coin from a jar that contains 14 quarters, 26 dimes, 12 nickels, and 8 pennies.
What is P(NOT dimes)?
34/60 = 17/30