Permutations
Permutations and Combinations
Fundamentals of Probability
Conditional Probability
Two-Way Tables
100
There are 7 performers who will present their comedy acts this weekend at a comedy club. One of the performers insists on being the last stand-up comic act of the evening. If this performer's request is granted, how many different ways are there to schedule the appearances?
What is 720.
100
Evaluate the given expression. 6C5 (combination: # of ways to combine 5 items from a set of 6, no repetition)
What is 6.
100
You are dealt one card from a standard 52-card deck. Find the probability of being dealt an 8.
What is 1/13.
100
A bucket contains 20 lottery balls numbered 1-20. Find the probability of getting an odd numbered ball given that it is a 2 digit number.
What is 5/11.
100
Define what the difference between joint frequency and marginal frequency is.
Joint frequency is the total inside the main box where two categories describe the box. Marginal frequency is the total of each singular category where the totals for each row and totals for each column are.
200
9P3 (permutation: number of ways to order 3 items from a set of 9, no repetition)
What is 504.
200
An election ballot asks voters to select three city commissioners from a group of eight candidates. In how many ways can this be done?
What is 56.
200
You are dealt one card from a standard 52-card deck. Find the probability of being dealt the ace of diamonds.
What is 1/52.
200
A card is randomly selected from a standard deck of playing cards. Find the probability that it is a 10 given that it is a red card?
What is 1/13.
200
If 74 students were surveyed on if they like Algebra and/or Geometry, what is the probability a student likes neither?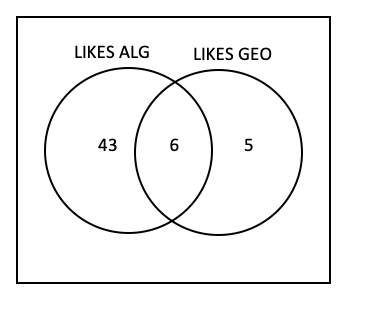 
74-43-6-5=20
20/74=0.27=27%
300
A club with 10 members is to choose three officers: president, vice-president, and secretary-treasurer. If each office is to be held by one person and no person can hold more than one office, in how many ways can those offices be filled?
What is 720.
300
A health inspector must visit 3 of 12 restaurants on Monday. In how many ways can she pick the 3 restaurants?
What is 220.
300
You are dealt one card from a standard 52-card deck. Find the probability of being dealt a diamond and a spade.
What is 0.
300
There are 90 students in my math classes. 32 take Algebra 2 and 30 take Geometry. 3 students take both Algebra 2 and Geometry. If a student is randomly selected, what is the probability that they are in Geometry given that they don't take Algebra 2.
What is 27/58.
300
What is the probability the student is a sophomore and prefers vanilla? 
Must use overlap!!
8/100 = 0.08 = 8%
400
At a benefit concert, thirteen bands have volunteered but there is only enough time for six of the bands to play. How many lineups are possible?
What is 1,235,520.
400
How many different four-letter passwords can be formed from the letters A, B, C, D, E, F, G, and H if no repetition of letters is allowed?
What is 1680.
400
A fair coin is tossed and a card is drawn. What is the possibility of getting heads and a red 10 card?
What is 1/26.
400
There are 50 student in football and 30 in wrestling. If 15 student are in both football and wrestling, what is the probability of selecting a student that is in wrestling given that he also plays football?
What is 3/10.
400
What is the probability a student is a junior or likes swirl ice cream?
42-4-15 = 23 juniors like swirl ice cream.
P(junior) + P(swirl) - P(overlap)
42/100 + 62/100 - 23/100=81/100 = 0.81=81%
500
In how many distinct ways can the letter of the word ROBBER be arranged?
What is 180.
500
Using 10 flavors of ice cream, how many cones with 3 different flavors can you create if it is important to you which flavor goes on the top, middle, and bottom?
What is 720.
500
Two cards are drawn from a deck of 52 cards. What is the probability of getting a black card or a king?
What is 7/13.
500
There are 50 slips of paper with numbers from 1-50 on them(each slip has one number). What is the probability of selecting a 2-digit number, given that it is prime.
What is 11/15.
500
If 74 students were surveyed on if they like algebra and/or geometry, what is the probability the student likes Geometry?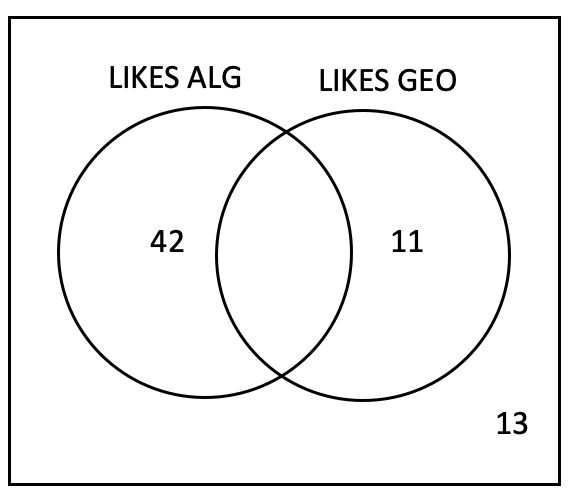
74-42-11-13=8
8+11 = 19 students like geometry
19/74=0.26=26%