`If `y=e^(kx)` then `dy/dx=?
dy/dx=ke^(kx)
`Rewrite using a power. `log_9 3=1/2
9^(1/2)=3
`Solve, giving your answer to 3sf ` 2^(3-2x)=88
-1.73
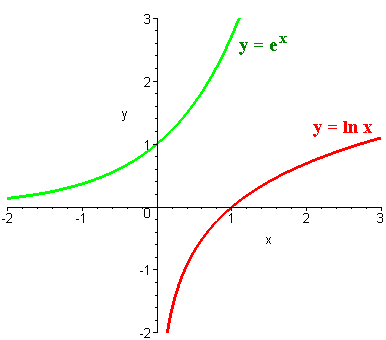
`Sketch the graph of `y=e^x` and `y=lnx` on the same grid. Label points of intersection with the axes.
`Complete the sentences. If `y=ax^n` for constants `a` and `n` then `logy=...` If `y=kb^x` for constants `k` and `b` then `logy=...`
logy=loga+nlogx. logy=logk+xlogb.
`Differentiate `e^x(e^x+1) ` with respect to `x.
2e^(2x)+e^x
State the multiplication, division and power laws of logarithms.
{(log_a x+log_a y = log_a xy),(log_a x-log_a y=log_a(x/y)),(log_a(x^k)=klog_ax):}
`Solve, giving your answer in exact form `e^(10x)-8e^(5x)+7=0
1/5ln7, 0
`Solve, giving your answer in exact form:` (lnx-1)^2=4
e^3
`Data are coded using `Y=logy` and `X=logx` to give a linear relationship. The equation of the regression line for the coded data is `Y=1.2+0.4X`. State whether the relationship between `y` and `x` is of the form `y=ax^n` or `y=kb^x.
y=ax^n
`The graph of `y=ka^x` passes through the points (1,6) and (4,48). Find the values of the constants `k` and `a.
k=3,a=2
`Write as a single logarithm and then simplify: `2log_10 2-(log_10 5+log_10 8)
log_10 (1/10)=-1
`Solve `log_5(x-3)=-1
3.2
`Solve `3^xe^(4x-1)=5`, giving your answer in the form `(a+lnb)/(c+lnd)
(1+ln5)/(4+ln3)
`The scatter diagram shows the relationship between two sets of coded data, `X` and `Y`, where `X=logx` and `Y=logy`. The regression line of `Y` on `X` is shown, and passes through the points (0,172) and (23,109). The relationship between the original data sets is modelled by an equation of the form `y=ax^n`. Find, correct to 3 decimal places, the values of `a` and `n.
a=1xx10^172, n=-2.739 ` (3dp)
`The population of a country is modelled using the formula `P=20+10e^(t/50)` where P is the population in thousands and t is the time in years after the year 2000. Use the model to predict the population in the year 2030.
38,221
`Given that `p=log_q 16`, express in terms of `p, {(a. log_q 2),(b. log_q (8q)):}
{(a. 1/4p), (b. 3/4p+1):}
`Solve, giving your answer to 4dp ` 7^(x+1)=3^(x+2)
0.2966
`Officials are testing athletes for doping at a sporting event. They model the concentration of a particular drug in an athlete's bloodstream using the equation `D=6e^(-t/10)` where D is the concentration of the drug in mg/l and t is the time in hours since the athlete took the drug. Find the concentration of the drug in the bloodstream after 2 hours.
4.91 mg/l
`Data are collected on the number of units (c) of a catalyst added to a chemical process, and the rate of reaction (r). The data are coded using `x=logc` and `y=logr`. It is found that a linear relationship exists between `x` and `y`and that the equation of the regression line of `y` on `x` is `y=1.31x-0.41.` Use this equation to determine an expression for `r` in terms of `c.
r=0.389c^1.31
`Nigel has bought a tractor for £20,000. He wants to model the depreciation of the value of his tractor, `£T`, in `t` years. His friend suggests the two models below. Interpret the meaning of the 1000 in model 2 and suggest why this might make model 2 more realistic. `{(1:, T=20000e^(-0.24t)),(2:,T=19000e^(-0.255t)+1000):}
`Given that `a` and `b` are positive constants, and that `a>b`, solve the simultaneous equations ` {(a+b=13),(log_6 a+log_6 b=2):}
a=9, b=4
`Given that `y=9^x` and `log_3 y=log_9 y^2`, solve the equation ` log_3(2-3x)=log_9(6x^2-19x+2)
x=-1/3, x=-2
`The graph of `y=3+ln(4-x)` is shown below. Calculate the exact coordinates of the `x`-intercept.
(4-e^-3,0)
`The table shows some data collected on the temperature, `t^oC`, of a colony of insect larvae and the growth rate, `g`, of the population. The data are coded using the changes of variable `x=t` and `y=logg`. The regression line of `y` on `x` is found to be `y=0.09+0.05x`. Given that the data can be modelled by an equation of the form `g=ab^t` where `a` and `b` are constants, find the values of `a` and `b.
a=1.23, b=1.12