Vocabulary
Proofs
Transformations
Shapes
Random
100
What is a regular polygon
A shape where all sides and angles are congruent
100
True or False: Corresponding parts of congruent triangles are congruent
True
100
How do you find the minimum number of degrees of rotation?
360/(# of sides)
360/n
100
What is the sum of the interior angles of any quadrilateral?
360o
100
ABC is a triangle, m<A = 117o, and m<C = 33o. What is the measurement of <B?
m<B = 30o
**Sum of all the angles of a triangle is 180o
200
What is a rigid motion?
A rigid motion is the act of taking an object and moving it to a different location without changing its size or shape
Partial Points for translations, reflections, rotations
200
Name all of the postulates that prove two triangles are congruent
1. SSS
2. SAS
3. ASA
4. AAS
BONUS (50 points): 5. HL
200
What is the rule to use for R270?
(x,y) ----> (y,-x)
200
What quadrilateral(s) have perpendicular diagonals?
1) Squares
2) Rhombi
3) Kites
200
ABCD is a trapezoid. If the m<D=3x+35, m<A=2x+95, and m<C=10x+25. Find the value of x and the m<B.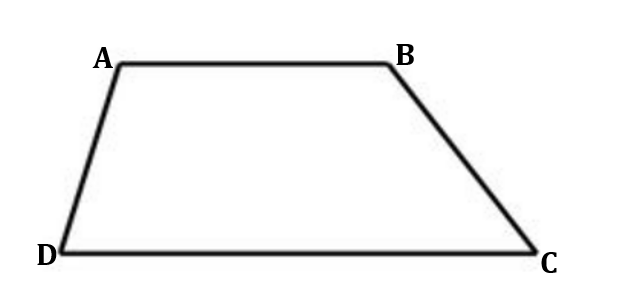
x=10
m<B=55o
300
A shape with 9 sides is called
Nonagon
300
Given the figures below, write the triangle congruency statement and name the correct postulate.
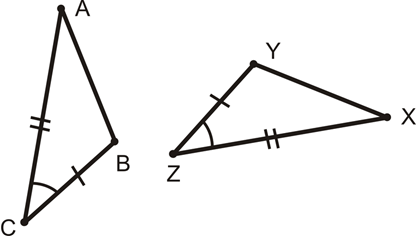
∆CBA≅∆ZYX
by SAS
300
What is the image of point (-2,7) after the transformation R-270 and what quadrant do you land in?
(-7,-2) landing in Q3
300
What is true about the diagonals of rectangles and squares but not rhombi?
The diagonals of a rhombus are not congruent
300
Triangle XYZ is an isosceles triangle, where XY is congruent to XZ. If the m<Y = 82o, find the m<X.
m<X = 16o
400
What shape has the following defintion: a quadrilateral with two pairs of congruent adjacent sides
A kite
400
What does CPCTC stand for and what must you prove first before using it?
Corresponding parts of congruent triangles are congruent; you must first prove that two triangles are congruent by a triangle congruency postulate.
400
What is the image of the point (-8,-4) under the translation T(-2,6)
(-10,2)
400
True or False: in all quadrilaterals diagonals bisect each other
False; only parallelograms have diagonals that bisect each other, this is not true for isosceles trapezoids and kites
400
In rhombus QUAD below, <QDR=6x+13 and <DQR=x+35. Classify triangle QRU
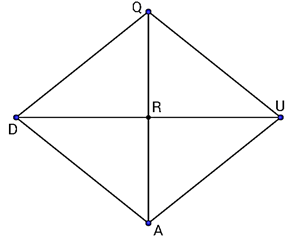
Triangle QRU is a right scalene triangle.
<RQU=41o, and <QUR=49o
500
What is a line of symmetry?
a line that can be drawn through a figure so that the figure can be mapped onto itself after a reflection across the line
500
Fill in the correct reasons for the proof below:
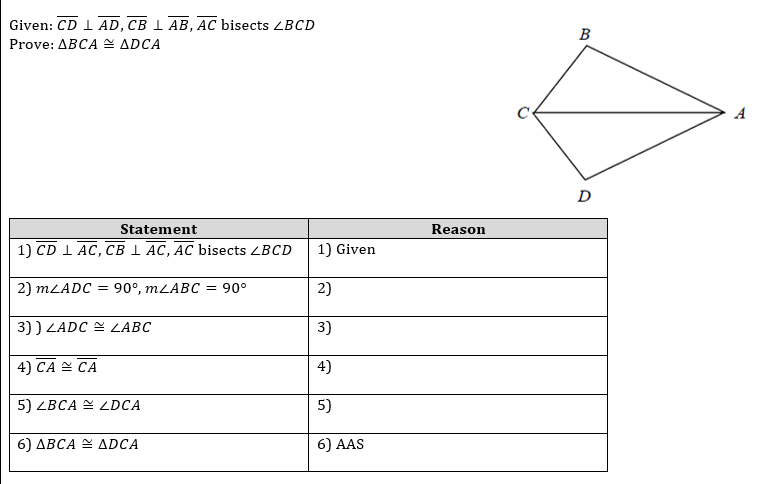
2.) Perpendicular lines defintion
3.) All right angles are congruent
4.) Reflexive Property
5.) Angle Bisector Defintion
500
There is a triangle, regular hexagon and a regular decagon that are all rotated about themselves. After a 180 degrees rotation, which of the shapes, if any, are mapped onto themselves?
The hexagon and decagon are mapped while the triangle is not.
500
Name the 5 properties that are true for all parallelograms
1) Opposite sides are congruent
2) Opposite sides are parallel
3) Opposite angles are congruent
4) Consecutive angles are supplementary
5) The diagonals bisect each other
500
Right triangle ABC is graphed below. If ABCD is a square, what is the length of diagonal BD?
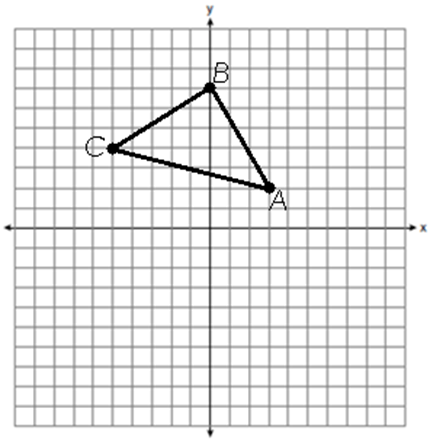
**Diagonals in a square are congruent**
2sqrt17