Factored Form
Vertex Form
Give me a Quadratic
SUPER HARDY HARD HARD!
100
Convert x2+6x+9 to factored form.
(x + 3)2
100
Tell me the vertex and axis of symmetry.
y = (x+3)2 - 9
Vertex at (-3, -9)
Axis of symmetry at x = -3
100
Give me a quadratic with a vertical stretch of 2, that has a maximum, and has x-intercepts at 2 and -7.
-2(x - 2)(x + 7)
This will face downward, so it will have a maximum.
100
Factor x2 + 3xy - 18y2
(x - 3y)(x + 6y)
200
Convert (2x +1)(x - 5) to standard form.
2x2 - 9x - 5
200
Complete the square on this quadratic, then tell me where the vertex is.
y = 3x2 - 18x + 27
There are 3 squares.
Divide by 3, then by 2.
3(x - 3)2 + 0
But is the zero necessary?
200
Give me a quadratic that has a stretch of 1/2 and also a y-intercept of 10.
The middle term can be anything.
1/2x2 + x + 10
200
An ball is launched at 19.6 meters per second (m/s) from a tall platform. The equation for the object's height s at time t seconds after launch is s(t) = −4.9t2 + 19.6t + 58.8, where s is in meters. You can graph this if you want.
What does the y-intercept represent in this story?
It would be (0, 58.8), which is at the beginning, before the ball was thrown, you were 58.8 meters high.
You were on the platform and hadn't thrown it yet.
300
Convert 2x2+10x-24 to factored form.
2(x2 + 5x - 24)
=2(x + 8)(x - 3)
300
Convert to standard form.
4(x + 1)2 - 9
4(x +1)(x + 1) - 9
=4(x2 + 2x + 1) - 9
=4x2 + 8x + 4 - 9
=4x2 + 8x - 5
300
Give me a quadratic with an axis of symmetry of 5 and has a vertex that is a minimum.
___(x - 5)2 +/- ______
The "a" and the "k" can be any number, but the "a" has to be positive so the vertex is a minimum.
300
Factor by grouping.
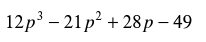
3p2(4p - 7) + 7(4p - 7)
(4p - 7)(3p2 + 7)
400
Convert (x - 1)2 + 14 to factored form.
Unfactorable!
400
Complete the square.
y = x2 + 7x + 12
(x + 3.5)2 - 0.25
400
Give me two different quadratics that BOTH have x-intercepts of 3 and -3.
(x - 3)(x + 3)
2(x - 3)(x + 3)
400
Write a graph that has the x-intercepts of 4 and 0.
y = x(x - 4) or (x + 0)(x - 4)
Any number can be in front.
500
Factor 3x2 - 16x - 12.
Multiply 3 and -12
What are factors of -36 that add to give you -16x?
-18 and 2
Use those in grouping or the box method.
(3x + 2)(x - 6)
500
Complete the square.
1/2x^2-8x+1
1/2(x-8)^2-31
500
An ball is launched at 19.6 meters per second (m/s) from a tall platform. The equation for the object's height s at time t seconds after launch is s(t) = −4.9t2 + 19.6t + 58.8, where s is in meters. You can graph this if you want.
What do the x-intercepts represent in this story?
The x-intercepts are (-2, 0) and (6, 0).
The x (or t) is seconds and the y (or s) is meters. (-2,0) doesn't make sense because you can't have -2 seconds. So (6, 0) means that after 6 seconds, the ball hit the ground (height is 0).
500
Make me a graph with a vertex of (-5, 9) and has a vertex as a maximum and a vertical stretch of 1.
Change it to general form.
Vertex form is -(x + 5)2 + 9
Then general form is -x2 - 10x - 16