Factoring
Vertex Form
y=a(x-h)^2+k
y=a(x-h)^2+k
Completing the
Square
Square
Quadratic Formula
Discriminant
100
Surprise! This question is actually worth 1000 points!!
Fully factor:
12ab^2c^3+18abc^2
6abc^2(2bc^2+3)
100
What are the coordinates of the vertex of
y=-3(x+4)^2-1
(-4,1)
100
What value would you need to add to both sides of the equation to solve by completing the square?
x^2-6x+ ?=-5+?
? = 9
100
What is the quadratic formula?
x=(-b+-sqrt(b^2-4ac))/(2a)
100
Find the discriminant of
x^2+6x+10=0
Discriminant = -4
200
Solve for x by factoring:
x^2-4x+3=0
x=1, 3
200
Describe how the graph of
y=-(x+5)^2-12
compares to
y=x^2
The graphs are congruent to each other (same size and shape). Every point on
y=x^2
was flipped over the x-axis, shifted 5 units to the left, and down 12 units.
200
Solve
(x+7)^2=5
x=-7+-sqrt5
200
What does the quadratic formula actually do?
The quadratic formula is used to solve for the x values that make quadratic equations in the form below true.
ax^2+bx+c=0
200
How long has Waynflete's longest serving faculty member been teaching at the school? (This is a current member of the faculty - double points for naming the person!)
45 years
Susan Nelson!!
300
Fully factor
xy^2-9xz^2
x(y-3z)(y+3z)
300
What color are the walls in our classroom (Morrill 25)?
Light blue / green (either or both colors are acceptable).
300
What value would you need to add to both sides of this equation to solve by completing the square?
3x^2+5x=3
25/36
300
Use the quadratic formula to solve for x:
2x^2-6x+5=0
x=(3+-i)/2
300
Use the discriminant to describe the nature of the roots of this quadratic. Be specific!
3x^2-8x-5=0
Two irrational roots (conjugates)
400
Write a quadratic equation in factored form that matches this graph:
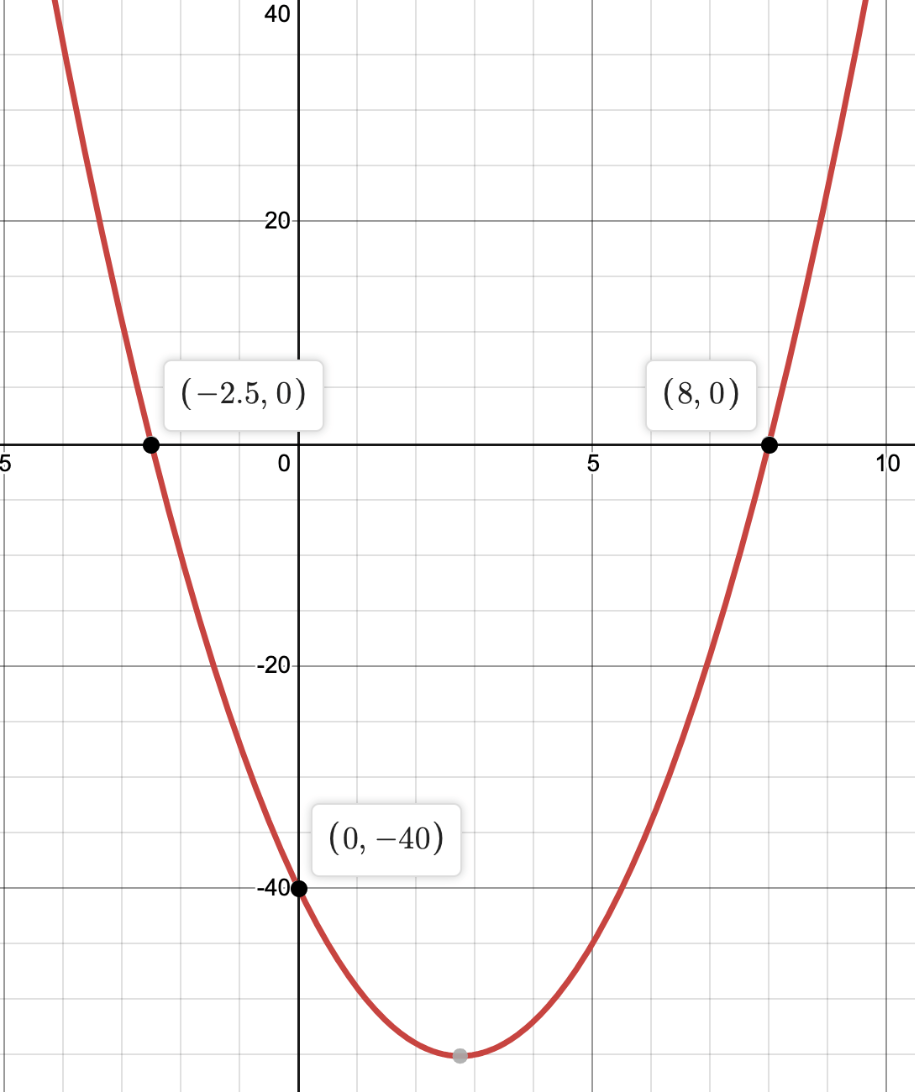
y=(2x+5)(x-8). or. y=2(x+5/2)(x-8)
400
Vertex form is:
y=a(x-h)^2+k
Find a, h, and k for the parabola graphed below:
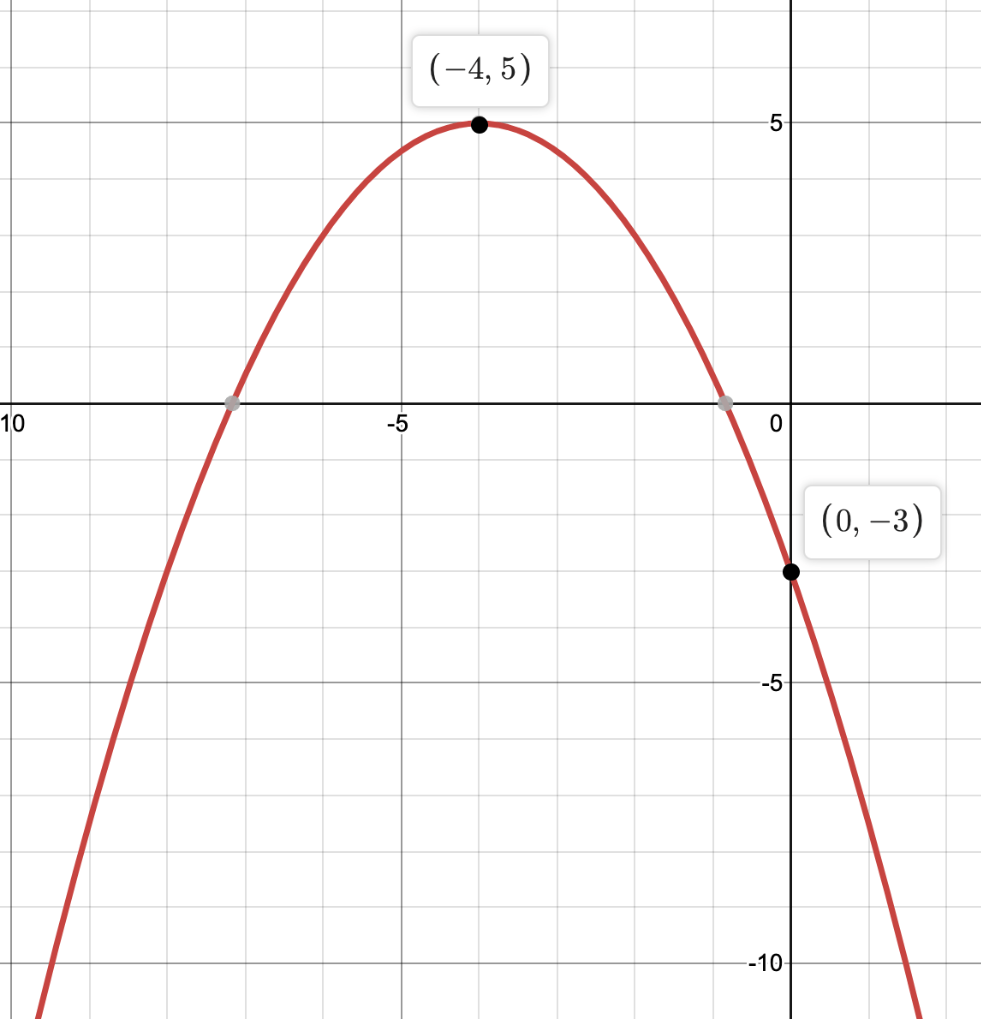
a = -1/2
h= -4
k = 5
400
What value would you need to add to both sides of this equation to solve by completing the square?
ax^2+bx+c=0
(b/(2a))^2=b^2/(4a^2)
400
A box with a height of (x+5) cm has a square base with sides of x cm. A second box with height of (x+2) cm has a square base with sides of (x+1) cm. If the two boxes have the same volume, find the exact value of x.
x=(5+sqrt33)/2 cm
400
Find the value of k that will yield just one solution to the quadratic.
kx^2-4x+8=0
k=1/2