Inequalities
Inequalities
Is the point (0, 0) a solution to the following quadratic inequality?
y=x^2+2x-6
Yes (True)
A negative a value does what to a parabola
Vertical reflection
The transformation that occurs in the quadratic function
f(x)=(x-3)^2
Horizontal translation right 3 units
Write the function in vertex form: y= x^2 +2x+5
y= (x+1)^2 +4
A quadratic function that has been vertically shifted up 3 units
y=x^2+3
Is the point (–2, 3) a solution to the following quadratic inequality? y ≥ x^2 + 2x + 3
Yes (True)
The h value of a parabola does what to it?
Translation left or right/Horizontal translation
The transformation that occurs in the quadratic function
f(x)=2x^2
Vertical stretch (scale factor = 2)
Write the function in vertex form: y = -x^2+2x+2
y= -(x-1)^2 +3
A quadratic function that has been horizontally shifted left 6 units
y=(x+6)^2
Graph
y<x^2
See whiteboards
The k value does what to a parabola?
Translation up and down/Vertical translation
The transformations from the parent function to the graph shown below
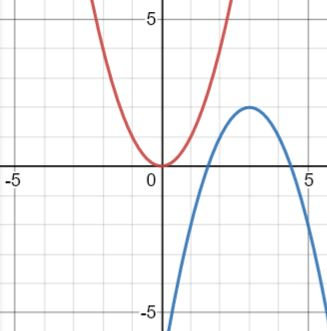
Reflection over the x-axis, a horizontal shift right 3 units, and a vertical shift up 2 units
Write the function in vertex form: y = -5x^2 +12
y = -5x^2 +12
A quadratic function that has been horizontally shifted right 2 units and vertically shifted down 5 units
y=(x-2)^2-5
Solve the inequality.
2x^2 + 3x <= 2
–2 ≤ x ≤ 1/2
If |a|>1, what transformation occurs?
Vertical stretch
The Transformations that Occur in the Quadratic Function
f(x)=1/3(x+2)^2-4
Horizontal translation left 2, vertical compression of 1/3, and a vertical translation left down 4
Write the function in vertex form: y=4x^2 + 7x
y=4(x+7/8)^2-49/16
A quadratic function that has been vertically shifted down 3 units, horizontally shifted left 6 units, and reflected over the x-axis
y=-(x+6)^2-3
Solve the inequality.
2x^2 + 2 > -5x
{x|x < –2 or x > –1/2}
If |a|<1, which transformation occurs?
Vertical compression
The transformations that occur in the quadratic function
f(x)=-5(x-3)^2+6
Horizontal translation right 3 units, reflection across the x-axis, a vertical stretch of 5, and a vertical translation up 6 units?
Write the function in vertex form:
y = 2x^2 + 8x -3
Find the maximum or minimum
y = 2(x + 2)^2 -11
Minimum = -11
A quadratic function that has been reflected over the x-axis, has been vertically stretched by a factor of 3, and has a vertex at (3,5)
y=-3(x-3)^2+5