How many solutions does this quadratic function have?
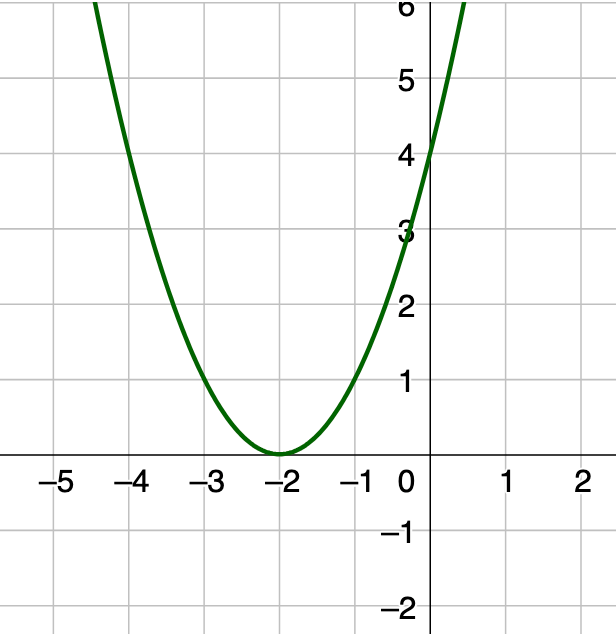
1
State the y-intercept.
6
Describe the transformation from
f(x) = x2 to g(x) = x2 + 6
g(x) shifted 6 units up
State the y-intercept.
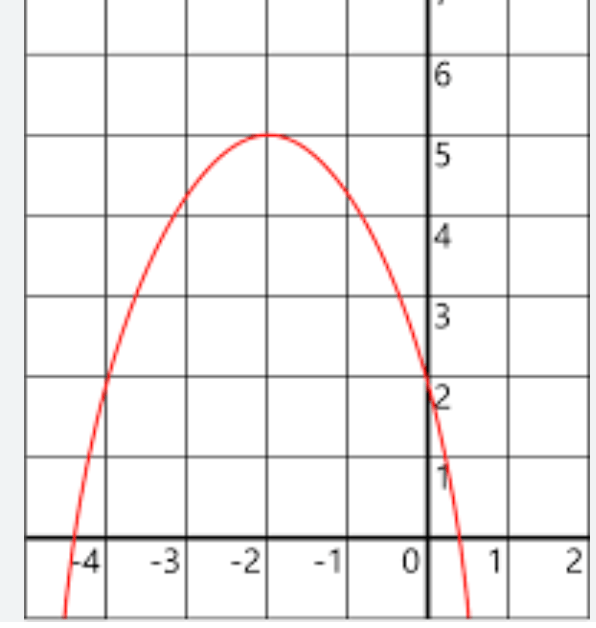
y = 2 or (0, -2)
Will the graph of f(x) = x2 - 3x - 4
open upward or downward?
upward
Does this quadratic have a maximum or a minimum?
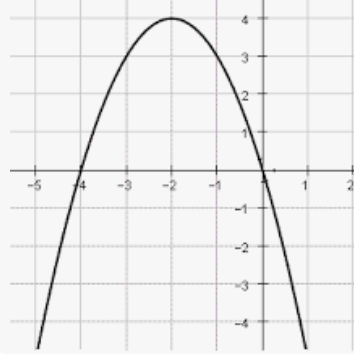
maximum
State the vertex.
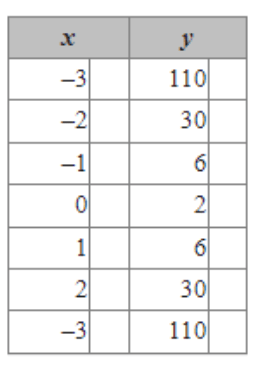
(0, 2)
Describe the transformation from
f(x) = x2 to g(x) = (x - 9)2
g(x) shifted 9 units right
State the zeros.
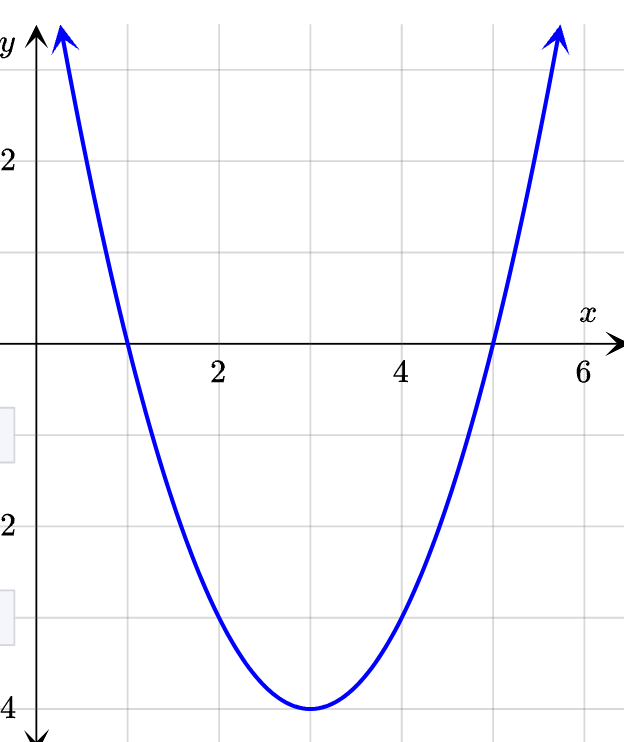
x = 1, x = 5
Describe the transformation from
f(x) = 2x2 to g(x) = 8x2
g(x) became narrower
State the roots(s) shown.
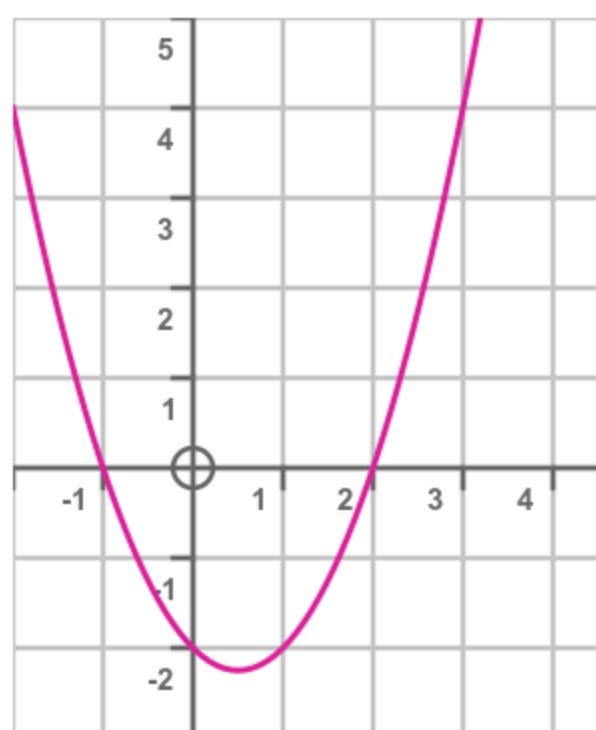
x = -1 and x = 2
State the vertex
(0, 1)
Describe the transformation from
f(x) = x2 to g(x) = 7x2
g(x) became narrower
State the vertex.
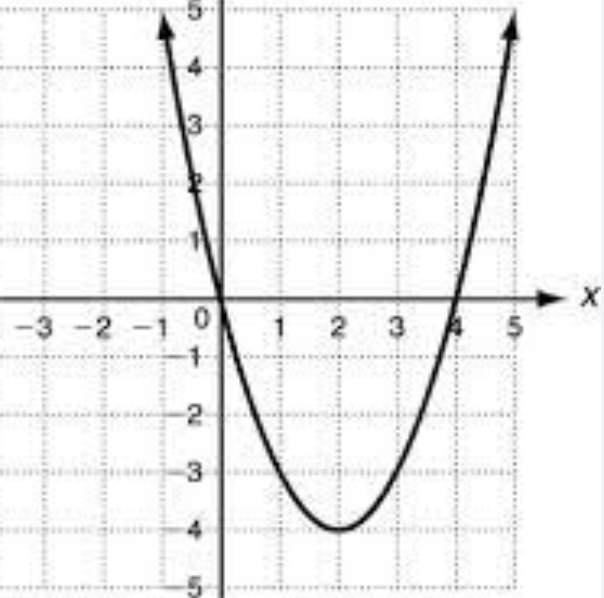
(2, -4)
State the minimum value.
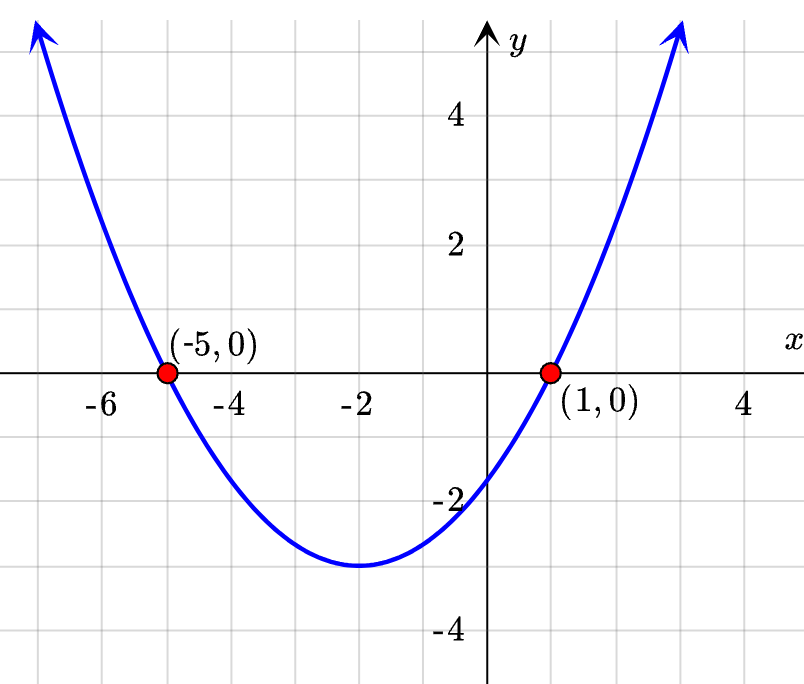
-3
State the vertex and state if it is a maximum or a minimum.
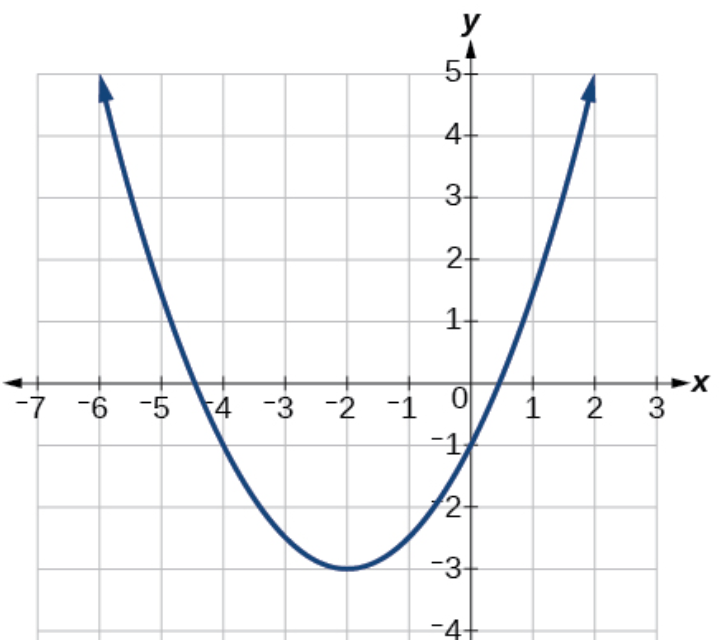
(-2, -3) - minimum
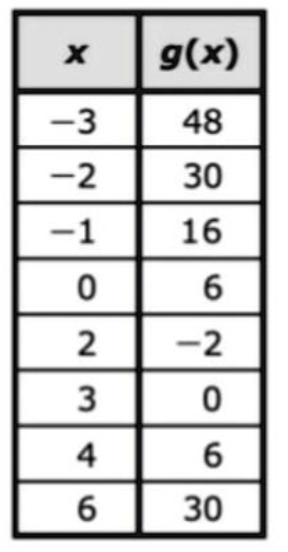
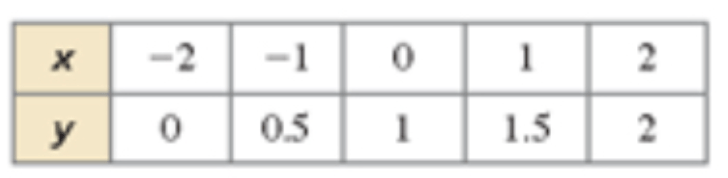
How many solutions are shown in the table? Name it/them.
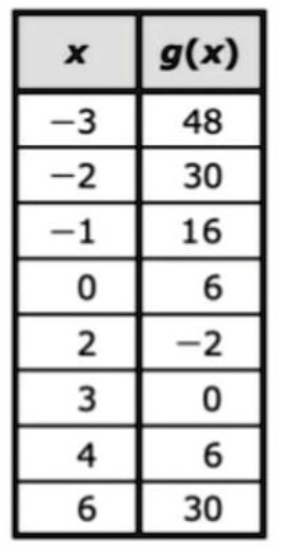
one. x = 3
Describe the transformation from
f(x) = x2 to g(x) = (x - 2)2 - 3
g(x) shifted 2 units right and 3 units down
State the maximum value.

7
Does the graph of f(x) = - x2 + 3x - 4
have a minimum or a maximum? Explain.
maximum
State the axis of symmetry.
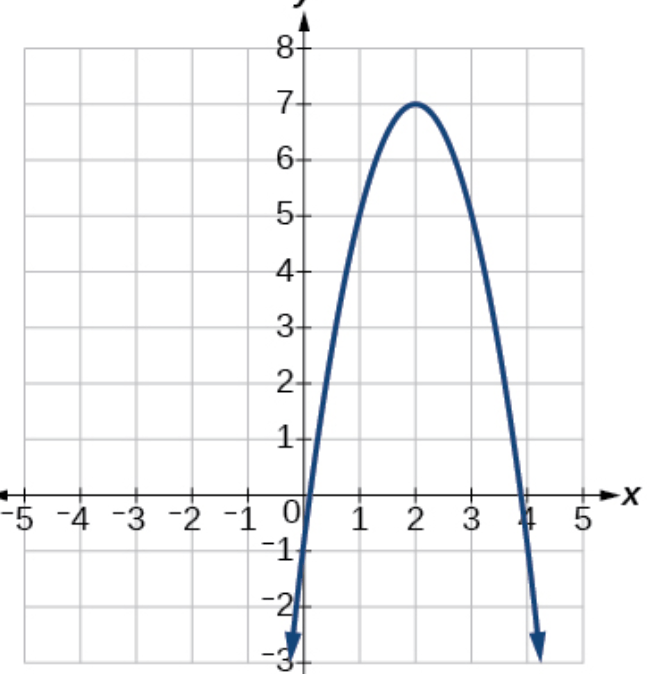
x = 2
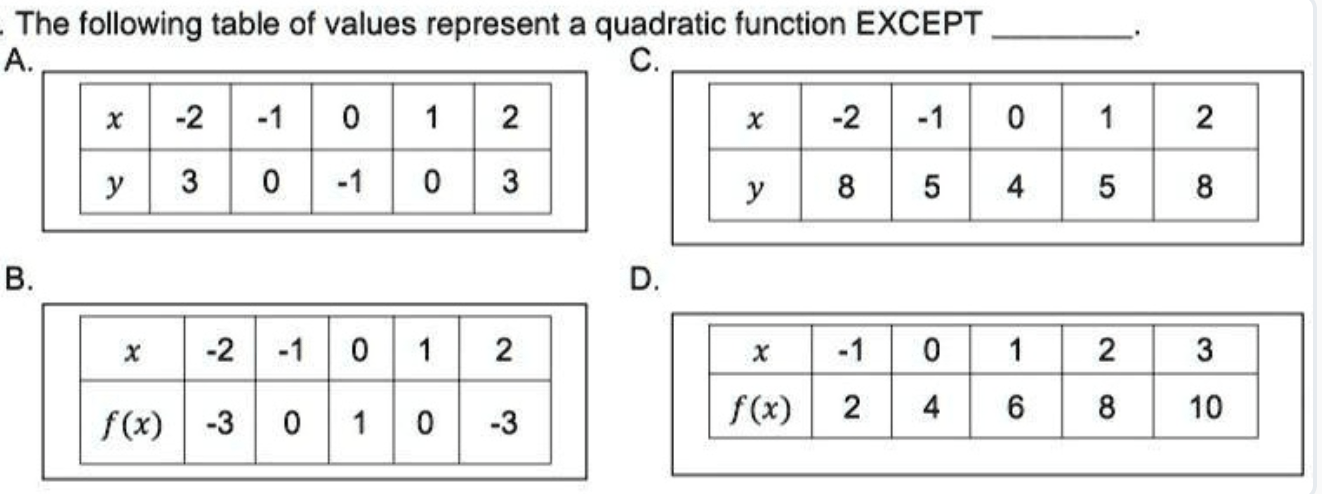
D.
Describe the transformation from
f(x) = x2 to g(x) = 3(x + 4)2 - 3
g(x) became narrower and shifted 4 units left and 3 units down
State the axis of symmetry.
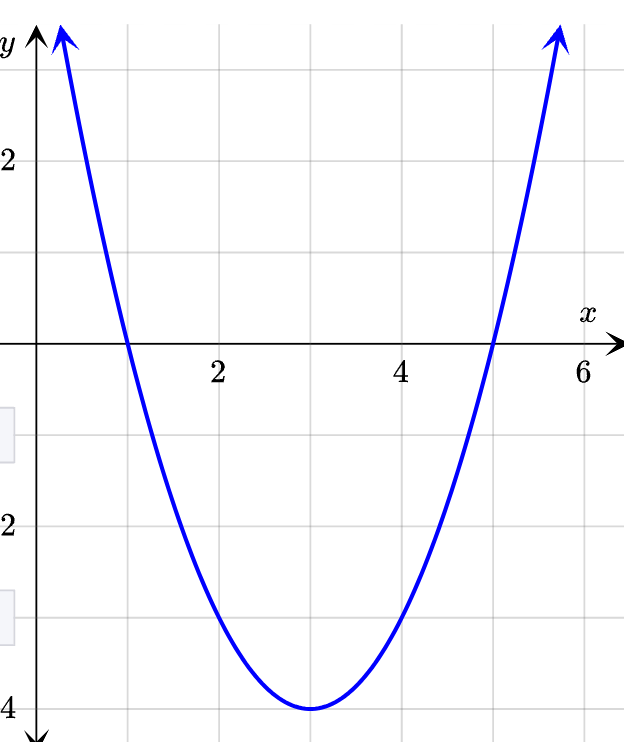
x = 3
State the solutions.
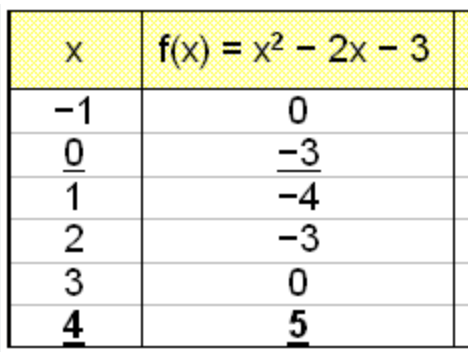
x = -1 and x = 3