f(x)=−(x−3)(x−5)
Find an equivalent form of the function f.
f(x)= -(x-3)(x-5)
f(x)=(-x+3)(x-5) <-- Negative is distributed
f(x)= -X² +5x +3x - 15 <-- Found using FOIL
f(x)= -X² +8x - 15 in Standard Form
or
f(x)= (x - 4)² + 1
h=-b/2a
h=-(-8) / (2*-1) = 4
Put x=4 into equation to find k:
k= -4² + (8 * 4) -15
k=1
Name three components needed to graph a quadratic function.
What is the quadratic formula?
What do p and q represent in intercept form?
y = a(x - p)(x - q)
How do you find the x-intercept of a quadratic formula?
Entering zero in the place of y:
Ex. 0= ax² + bx + c
Find the factors of the following equation:
x²+3x+2 = 0
(x + 2)(x + 1)= x²+3x+2
This is because 2 and 1 are the only numbers that multiply into 2 and add up to 3.
Draw the graph of the following function:
-x² - 2x + 3 = f(x)
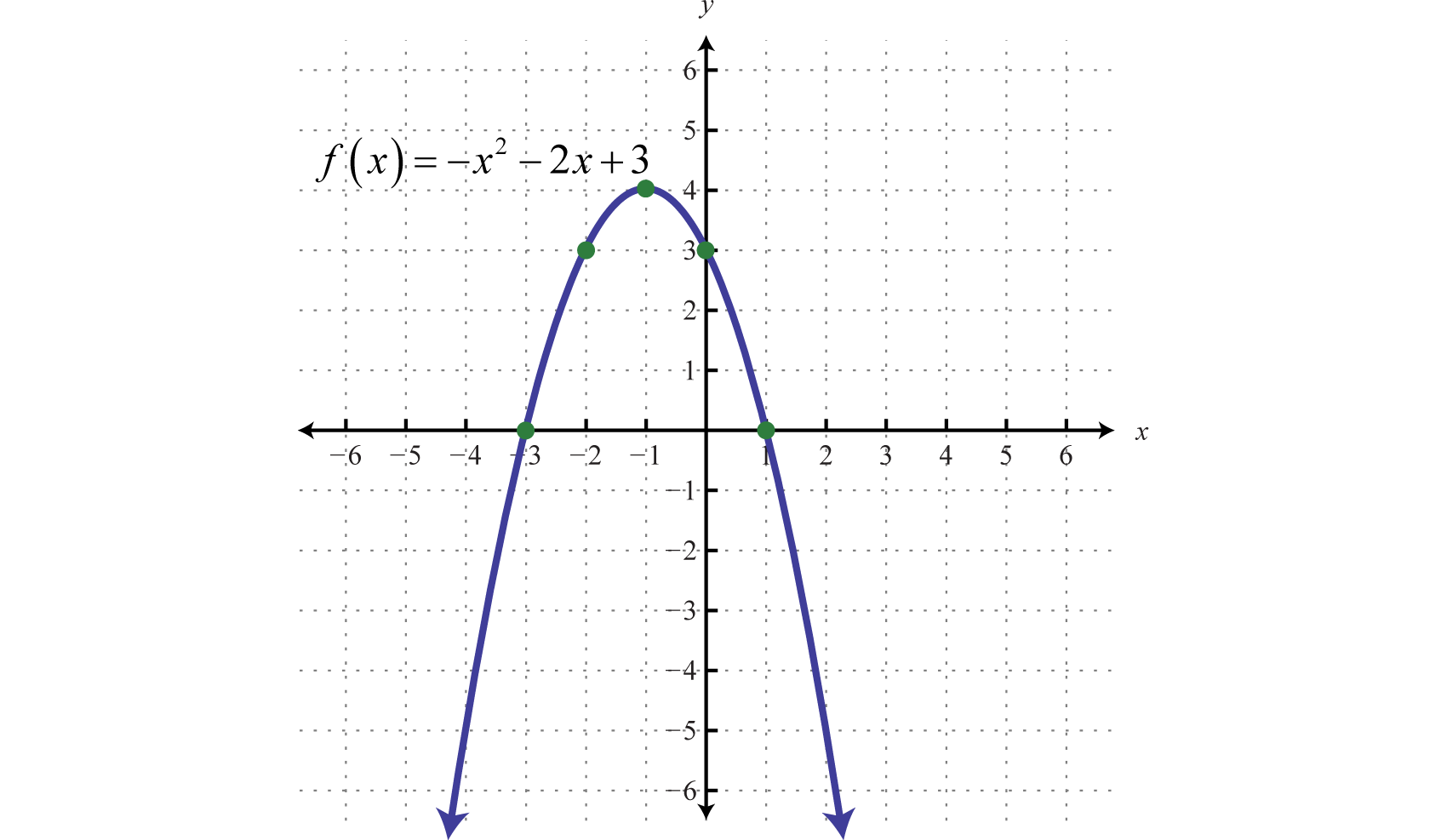 Line of symmetry falls on (-1,- 4) because of 2x value (as seen after experimenting on graph)
Line of symmetry falls on (-1,- 4) because of 2x value (as seen after experimenting on graph)
-x² implies negative parabola
What is Vertex Formula?
f(x) = a(x – h)2 + k
f(x) = (-x+2)²
g(x) = -4x² + 16x -16
Do the functions f(x) and g(x) share vertex coordinates?
Yes, we can see how g(x) is negative four times f(x), with g(x) being a reflection on the x-axis.
(-x+2)(-x+2)
x² - 2x -2x +4
f(x) = (-x+2)² = x² - 4x +4
-4(x² - 4x +4) = -4x² + 16x -16 = g(x)
Though f(x) is positive and g(x) is negative they share a vertex.
How do you find the y-intercept of a quadratic formula?
Entering zero in the place of all x-values:
Ex. f(0)= a(0)² + b(0) + c
Find the sum of all coefficients in the following function:
g(x)=7000x² + 34x - 400
7034
Draw the graph of the following equation:
f(x)= x² - 3
We can draw this function but first drawing f(x)=x², we can then translate the function f(x)=x² three units up the y-axis.
(v+1/5)²−9=0
Find the sum of all solutions to the function.
(v+1/5)²−9=0
+9 +9
(v+1/5)²=9
SquareRoot ((v+51)²)= SquareRoot (9)
v+1/5 = 3
v= +-3 - 1/5 or v= 3 +- 1/5
Sum:
(-1/5+ 3) + (-1/5-3)= (-2/5)
g(x) = -4x² + 16x -16
Find the vertex of g(x)
X-vertex = -16/(2*-4) --> X-vertex = 2
For Y vertex we can plug in X vertex
g(2)= -4(2²) + (16*2) - 16
g(2)= 0
Vertex: (2, 0)
Name the x-intercepts y=x² - 3x + 2
0= x² - 3x + 2
Using the quadratic formula we get:
3 +- SquareRoot (-3² - 4*1*2)/2
We get:
X= 1
X=2
What does the value of the coefficient a tell us about any given function?
A value smaller than 1 lead to a skinner parabola.
A value greater than 1 leads to a wider parabola.
Find g(f(5)) given:
g(x) = 2x²+3x+10
f(x)=x/10
2(5/10²) + 3(1/2)+ 10= 12
g(f(x))= 5
1−9b²=0
List all solutions to the function above.
1−9b²=0
-1 -1
-9b²=-1
9b²=1
SquareRoot (9b²)= SquareRoot (1)
3b = +-1
b= -1/3 and b = 1/3
p+1 and q-1 are roots to the function f(x)= x² + 4x - 12
Find p and q.
f(x)= x² + 4x - 12 factors to f(x) = (x-2)(x+6)
x=2
x=-6
Consider the first-factor p and the second-factor q:
(p+1) =2 --> p=1
(q-1) --> -6 --> q=-5
Name the y-intercept y=x² - 3x + 2
y=x² - 3x + 2
y=(0²) -3(0) +2
y= 2
Describe the relationship between the vertex and the axis of symmetry.
The axis of symmetry is the line of symmetry found in the middle of the parabola. The axis of symmetry is either one x value or one y value. The vertex is a coordinate that described the highest or lowest point in the function. It has an x and y value in the coordinate. The line of symmetry showcases one of the two values depending on how it is structured: In the case of quadratic functions, the line of symmetry is always on the x-axis.
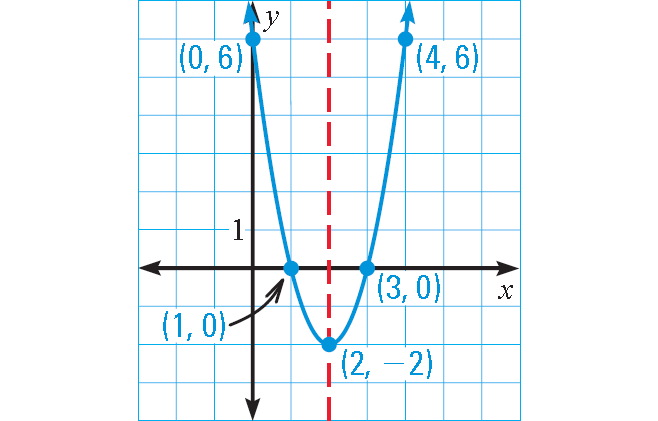 What is the equation of this graph in standard form?
What is the equation of this graph in standard form?
(X+1)(X-3)
Distribute using FOIL
X² -3x + 1x -3
X² -2x -3 = 0
Find the sum of the following answers:
a.) Mrs. Naik throws a ball into the air and times how long it takes for the ball to hit the ground, modeled by:
f(x)= -(x-3)² + 15
In how many seconds will the ball hit the ground?
b.) Hamza is studying ants in a part of an area (in hundreds) as a function of temperature in degrees Celsius modeled by:
g(x) = −4(x−6)²+400
What is the maximum number of ants in the area?
c.) Grace is flying a drone that that flys off of a platform. Its height (in feet) is measured by the function h(x), x seconds after take off, modeled by:
h(x)= −3(x−4)²+110
What is the height of the drone at the time of take-off?
a.) Using the Quadratic formula we get:
x=-6 +- SquareRoot(6^2 - (4*-1*6))/-2
Using GDC we get:
x=-0.87299
x=6.873 Seconds
Time cannot be negative: x = 6.873
b.) g(x) is in the Vertex form, therefore, we can identify the vertex as the maximum point of the parabola (g(x) also has a negative parabola).
x=400 Ants
c.) h(0) helps us find the height at the time of take off.
h(0)= -3(0-4)² +110
h(0)=-3(16) +110
h(0)= 62 feet
Sum: 6.873 + 400 + 62 = 468.873
Find the Vertex of the following function.
k(p)= 2k² - 3k + 1
h = -b/2*a
h = 3/2*2
h= 0.75
Plug into function:
2(0.75²) + -3(0.75) +1 = -0.125
(h,k)= (0.75, -0.125)
Find the sum of both x-intercepts and the y-intercept of the following function:
h(x)= x² + 7x -14
We can use the GDC to make the process more efficient:
x= -8.62
x= 1.623
y-intercept= -14
-8.62 + -14 + 1.623 = -20.997
Sum = -21