Quadratics in Standard Form
Quadratics in Vertex Form
Quadratics in Factored Form
Conversions
Graph
100
The standard form of quadratics
y=ax^2+bx+c
100
The vertex form of quadratics
y=a(x-h)^2+k
100
The factored form of quadratics
y=a(x-r)(x-s)
100
The process to convert quadratics in standard form to quadratics in vertex form
completing the square
100
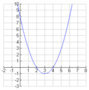
What is the vertex ?
(3,-1)
200
The value of y -intercept of quadratics in standard form
y=c
200
Values of a to reflect
y = a (x - h)^2 + k
a < 0
200
The factored form of
x^2-6x+8
(x-2)(x-4)
200
What is the vertex of the equation
y= (x-12)2+7 ?
(12, 7)
200
Quadratic equations take the shape of a what when graphed.
u
300
The y-value of
y = x^2 + 2x + 1 at
x=-4
y=9
300
The vertex of
-2 (x + 4)^2 + 2
(-4,2)
300
Formula to find x -value from the factored form
y=(x-r)(x-s)
x_{\text{vertex}} = \frac{r + s}{2}
300
When x2 is changed to x2 -3, the graph
Shifts down 3 units.
300
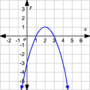
How many solutions does this graph have?
No solution
400
Special Term of
y=a^2 + 2ab + b^2
The perfect square trinomial
400
The y -intercept of
y = 2(x+3)^2 - 8
y=10
400
The equation an which the quadratic reflects its self?
Axis of symmetry
400
A parabola has a vertex at (-3,2). Where is the axis of symmetry?
x = -3
400
Name the zero ?
0 and 4
500
Special term of
y=a^2-b^2
Difference of squares
500
Transformation(s) of
-4 (x + 6)^2 - 4
1. vertical stretch by a factor of 4
2. vertical shift 4 units down
3. horizontal shift 6 units left
4. vertical reflection (flipped upside down)
500
How does the value for "h" transform a graph?
Horizontal Shift
500
Does the graph of
-2(x + 5) + 2
have a minimum or a maximum?
Maximum
500
what is the solution ?
1 and 3