Vertex Form
Standard Form
Intercept Form
Radicals/Complex Numbers
Factoring
100
Does this graph open facing upward (smiley)
or open facing downward (frown)?
y = -1/2(x+8)^2 + 5
downward
100
Identify the a, b, and c values:
4x^2-5=24x
a=4
b=-24
c=-5
100
What are the x-intercepts?
y=(x-6)(x+2)
x=6
x=-2
100
simplify the radical
sqrt(60)
2sqrt(15
100
What is the GCF of the following three terms?
12x^2
30x^5
24x^3
6x^2
200
How is this being translated?
y = (x-4)2+6
translated right 4 units
translated up 6 units
200
What is the axis of symmetry of the following quadratic:
y=2x^2-8x+12
x=2
200
What is the axis of symmetry?
y=(x-7)(x+3)
x=-2
200
simplify the radical
4sqrt(-72)
24isqrt(2)
200
Factor the following:
22x^3-14x^2
2x^2(11x-7)
300
What is the equation of the quadratic described by the following transformations from the parent function:
- translated 5 units down
- translated 3 units left
- reflected over the x-axis
- vertically compressed by a factor of 1/3
y=-1/3(x+3)^2-5
300
What is the vertex of the quadratic:
y=1/2x^2+10x+15
(-10, -35)
300
Convert this quadratic to intercept form:
y=x^2+4x-21
y=(x-3)(x+7)
300
simplify as much as possible
(4sqrt(3))/(6sqrt(5))
(2sqrt(15))/15
300
Factor the following:
9x^2-64
(3x+8)(3x-8)
400
What is the equation of this graph in vertex form?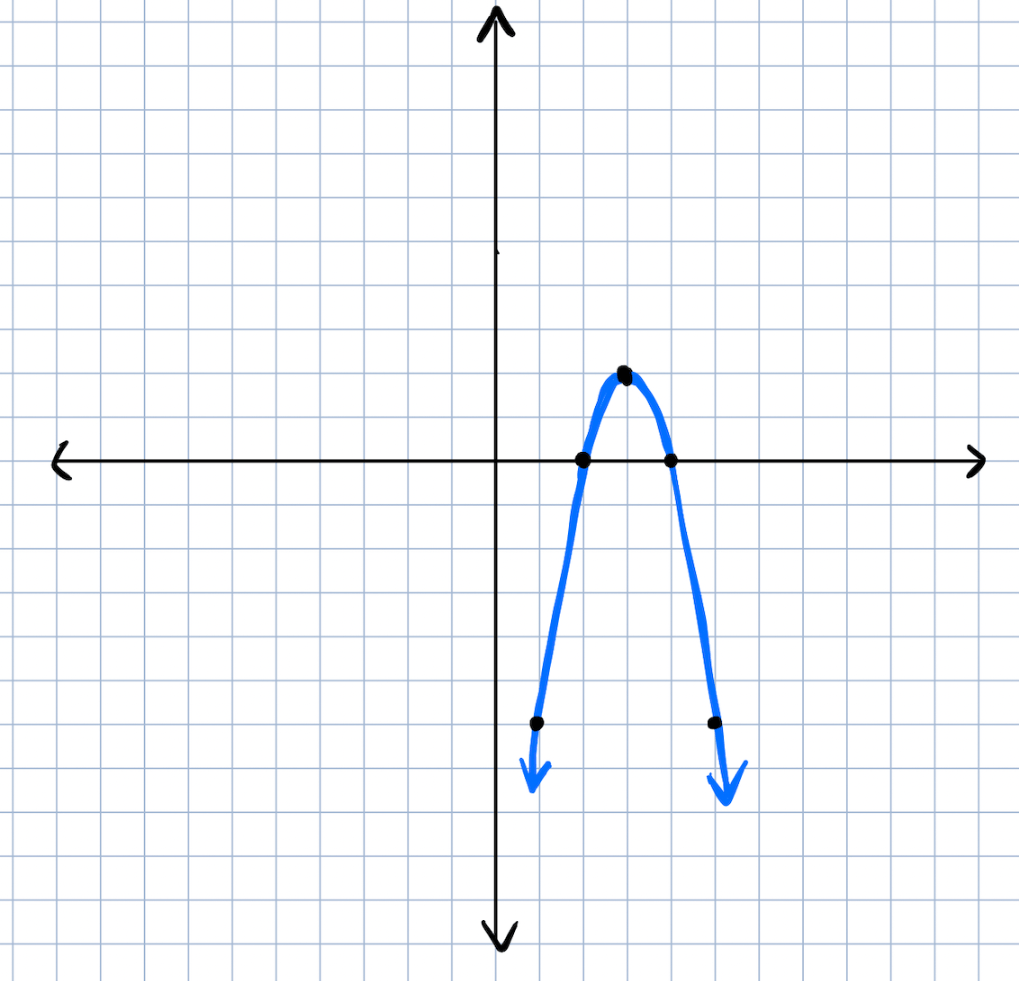
y=-2(x-3)^2+2
400
What are the x-intercepts of this quadratic:
y=2x^2-x-15
(-5/2, 0) and (3, 0)
400
What is the equation of this graph in intercept form?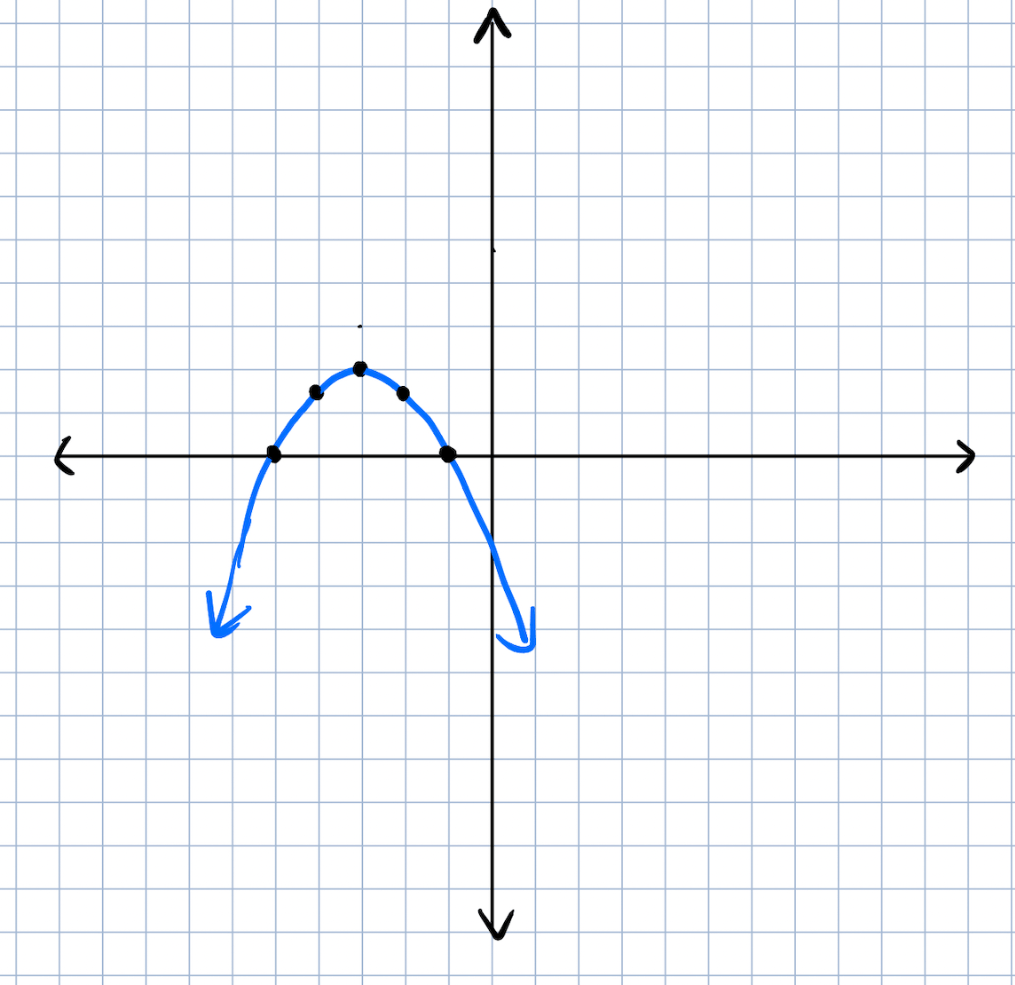
y=-1/2(x+5)(x+1)
400
simplify as much as possible
6/(2+4i)
(3-6i)/5
400
Factor the following:
3x^2-24x+36
3(x-2)(x-6)
500
Convert from standard form to vertex form:
y=x^2-8x+11
y=(x-4)^2-5
500
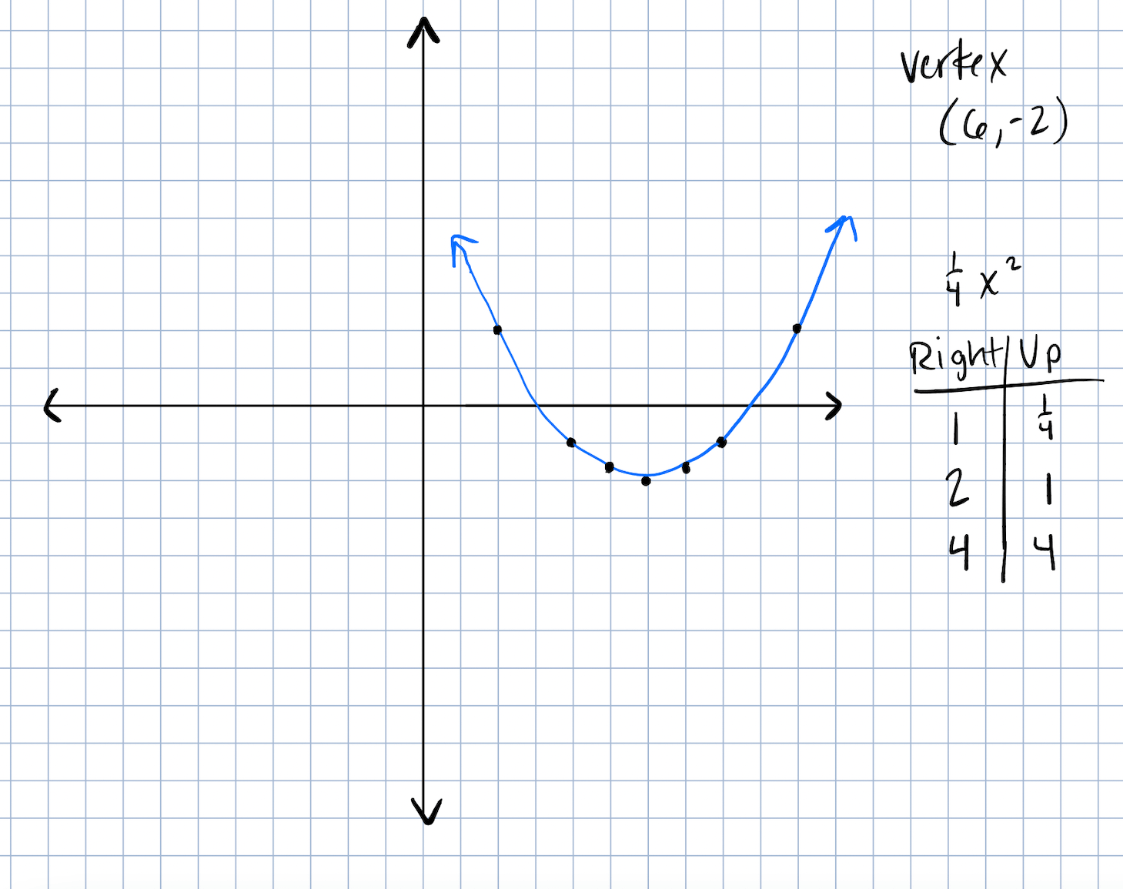
Graph the quadratic using a min. of 5 points
y=1/4x^2-3x+7
Must show all work, including:
- computations for finding vertex
- scale factor chart
500
A quadratic has x-intercepts of (3, 0) and (-1, 0) and goes through the point (2, -6). What is the equation of this quadratic written in intercept form?
y=2(x-3)(x+1)
500
simplify as much as possible
(3+2i)/(5-4i)
(7+22i)/41
500
Factor the following:
6x^3-22x^2-8x
2x(3x+1)(x-4)