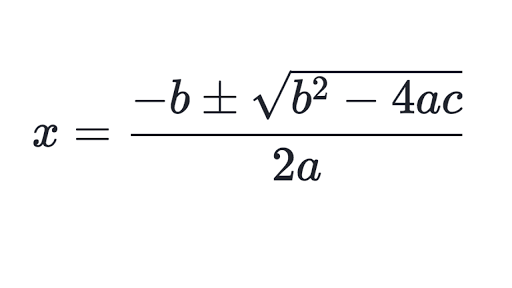Solving by factoring
Completing the square
Quadratic formula
Vertex form
Applications
100
Solve this quadratics by factoring.
x2 + 2x = 3
x2 + 2x - 3 = 0
= (x-1)(x+3) = 0
x = 1 or x = 3
100
Solve.
3x2 - 12x - 96 = 0
x = 8, x = -4
100
The discriminant tells you the _________ and ________ of the roots
number and nature
100
What is the vertex of y =( x -4)2 + 7 ?
(4,7)
100
A rock is thrown from a 33 foot cliff. If the height of the rock, h, at a given time, t, in seconds can be modeled by the function h(t) = -16t2 +33, how long was the rock in the air? Round to the nearest 10th of a second.
The rock was in the air for about 1.4 seconds
200
Solve this quadratic equation by factoring.
X2 + 16 = 10x
x2 - 10x + 16 =0
(x-2)(x-8)
x = 2 or x = 8
200
x2 + 9x + p = 7, find p that makes the left side of the equationa perfect square trinomial
p = 81/4
200
Find the discriminant adn describe the number AND nature of the roots.
6x2 - 17x = -21
Discriminant is -215, 2 imaginary roots
200
What is the vertex of (x+9)2 - 40 = y
((-9,-40)
200
After scoring the game winning touchdown, a football player spikes the ball. The path of the ball can be modeled by the function f(t) = -16t2 + 15t + 8. Use the discriminant to determine if the football reaches a height of 12 feet after it has been spiked. Justify your answer mathematically.
The discriminat is -31, therefore there are 2 imaginary solutions to this problem. The football will NOT reach a height of 12ft.
300
Solve this quadratics equation by factoring.
18x2 - 3x = 6
18x2 - 3x -6 = 0
= 3(6x2 - x - 2) = 0
= 3(3x -2)(2x +1)= 0
= 3x -2 = 0 2x + 1 = 0
x = 2/3 or x -1/2
300
Solve.
(x+6)2 = -18
x = -6 ±3i√ 2
300
Solve x2 - 8x + 14 = 0 using the quadratic formula.
x = -(-8) ±√ (-8)2 - 4(1)(14) / 2(1)
= (8 ±2√ 2)/ 2
= 4 ±√ 2
300
Put the following in vertext form by completing the square method:
y = x2 + 12x + 32
y = (x + 6)2 - 4
300
Freddie Freeman hits a walkoff grand slam in the World Series. The path of the baseball can be modeled by h(t) = -12t2 +37t + 6, where h(t) represents the height in feet and t is time in seconds. What was the maximum height of the ball. Round to the 100th.
The maximum height of the ball was 34.52 feet.
400
Factor completely, then solve.
6x2 + x = 35
(2x+5)(3x-7) = 0
x = -5/2 x = 7/3
400
Solve x2 − 6x − 3 = 0 by completing the square.
x2−6x=3
x2−6x+(−3)2=3+9
(x−3)2=12
x−3=±√12
x=3 ±2√3
400
Solve x2 + 4x - 21 = 0 by using quadratic formula.
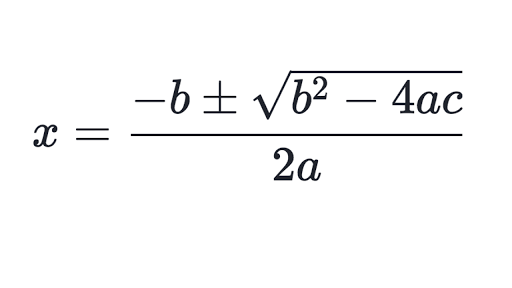
x = 3 or -7
400
Put the following in vertex form by completing the square:
y = 4x2 + 24x + 38
y= 4(x+9)2 +2
400
Freddie Freeman hits a pop fly that is not caught in the outfield. The path of the baseball can be modeled by h(t) = -12t2 +37t + 6, where h(t) represents the height in feet and t is time in seconds. How long was the ball in the air? Round to the nearest 10th of a second.
The ball was in the air for 3.2 seconds
500
Factor completely, then solve.
8n2 - 98 = 0
2(2n+7)(2n-7) = 0
n = -7/2 n = 7/2
500
Solve 2x2 - 12x + 22 = 0
Divide all terms by 2
x2 - 6x = -11
x2 -6x + (3)2 = -11 + 9
x2 -6x + 9 = -2
(x-3)2 = -2
x -3 = ± i√2
x = 3± i√2
500
Solve 2x2 = 3x - 6 by using quadratic formula.
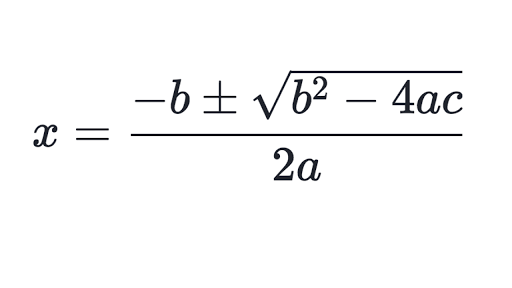
x = -(-3) ±√(-3)2 -4(2)(6) / 2(2)
x = (3 ±√ -39)/4
x =3/4 ± i√ 39/4
500
Put the following in vertex form by completing the square:
y= -2x2 + 8x -18
y = -2(x-2)2 - 10
500
A water baollon is dropped from the roof of a building that is 70 ft tall. How long does it take the balloon to pass by a 3rd floor window, 30 feet above the ground. Use the function h(t) = -16t2 + 70
It will take about 1.6 seconds for the ballon to pass the 3rd floor window.