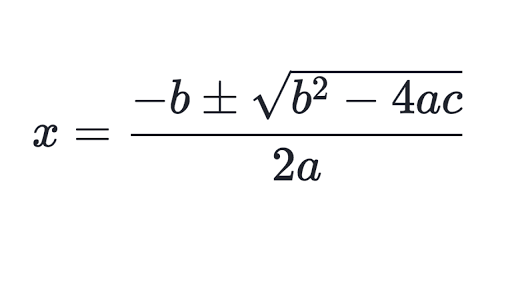Solving by factoring
Completing the square
Quadratic formula
Solving by taking square roots
Solve by Graphing
100
Solve this quadratics by factoring.
x2 + 2x = 3
x2 + 2x - 3 = 0
= (x-1)(x+3) = 0
x = 1 or x = 3
100
Is Completing the square a method used to solve a quadratic equation by changing the form of the equation so that the left side is a perfect square trinomial?
(Yes or no)
Yes
100
Is this quadratic formula?
Yes
100
Solve this equation by taking square roots.
x2 + 1 = 26
x2 = 25
x= 5, -5
100
Graph y = 2x^2 -3x +7
See board
200
Solve this quadratic equation by factoring.
X2 + 16 = 10x
x2 - 10x + 16 =0
(x-2)(x-8)
x = 2 or x = 8
200
What's the first thing you have to do to complete the square?
Divide all terms by the leading coefficient
ax2 + bx + c =0
200
Are these steps right?
Step 1. Identify a, b, and c and plug them into the quadratic formula.
Step 2. Use the order of operations to simplify the quadratic formula.
Step 3. Find the positive answer only.
No - both answers work. (Negative answers are OK too)
200
Solve this equation by taking square roots.
(x-4)2 - 16 = 0
(x-4)2 = 16
x- 4 =± 4
x = 0 or 8
200
When will a quadratic inequality have a solid parabola?
When it is <= or >=
300
Solve this quadratics equation by factoring.
18x2 - 3x = 6
18x2 - 3x -6 = 0
= 3(6x2 - x - 2) = 0
= 3(3x -2)(2x +1)= 0
= 3x -2 = 0 2x + 1 = 0
x = 2/3 or x -1/2
300
What do you have to do after first step to complete the square?
Step 2. Move the c value term to the right side of the equation.
Step 3. Add (b/2)^2 to both sides.
Step 4:Write as a perfect square.
Step 5. Take the square root on both sides of the equation.
Step 6. Finish solving for x.
300
Solve x2 - 8x + 14 = 0 using the quadratic formula.
x = -(-8) ±√ (-8)2 - 4(1)(14) / 2(1)
= 8 ±√ 8 / 2
= 5.41 and 2.59
300
Solve this equation by taking square roots.
(x+7)2 - 11 = 0
(x+7)2 = 11
x + 7 = ±√11
x = -3.68 and -10.32
300
When will a quadratic inequality have a dashed parabola?
When it is strictly > or <
400
What's the first step to solve quadratics by factoring
Step 1. Write the equation in standard form.
400
Solve x2 − 6x − 3 = 0 by completing the square.
x2−6x=3
x2−6x+(−3)2=3+9
(x−3)2=12
x−3=±√12
x=6.46 and -.46
400
Solve x2 + 4x - 21 = 0 by using quadratic formula.
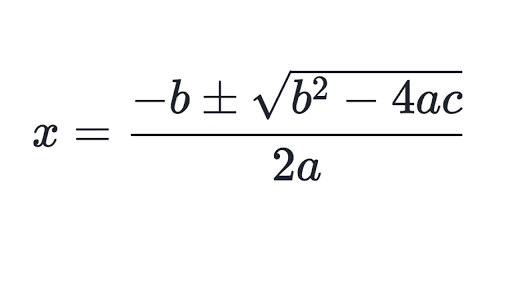
x = 3 or -7
400
What do you have to do first to solve quadratics equation by taking square roots?
Isolate the square.
400
Graph the following: y = 3(x - 4)^2 +8
See board.
500
What do you have to do after write the equation in the standard form?
Step 2. Factor completely.
Step 3. Use the zero product property.
Step 4. Solve each factor to get the x.
500
Solve x2 - 6x + 7 = 0
x2 - 6x = -7
x2 -6x + (3)2 = -7 + 9
x2 -6x + 9 = 2
(x-3)2 = 2
x -3 = ± √2
x = 4.42 and 1.59
500
Solve 2x2 = 7x + 6 by using quadratic formula.
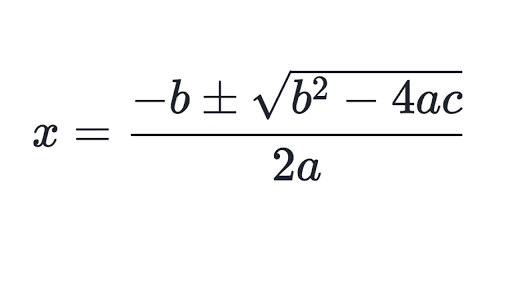
x = -(-7) ±√(-7)2 -4(2)(-6) / 2(2)
x = (7 ±√ 97) / 4
x =4.21 and -.71
500
What do you have to do to solve quadratics equation by taking square roots after step 1?
You have to take the square roots both sides. After that, solve the square roots and sole for x.
500
Graph the following: f(x) = -3(x -4)(x - 6)
See board.