y = x2
(0, 0)
x2+5x+4
(x+1)(x+4)
(x+3)(x+1)
x2+4x+3
If the radicand b2-4ac is positive, how many zeros are there?
2 solutions (2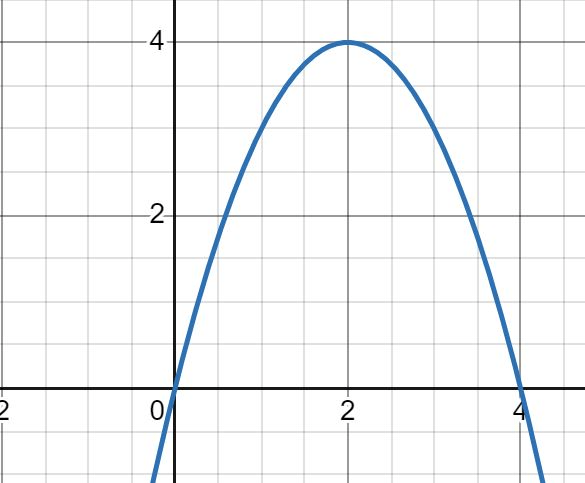 zeros)
zeros)
(x+2)(x-3)
x = -2 and 3
f(x) = (x-3)2 + 4
(3, 4)
x2+5x+6
(x+2)(x+3)
(x+2)(x-3)
x2-x-6
√(b2-4ac) / 2a is negative, there are this many zeros
zero (none) 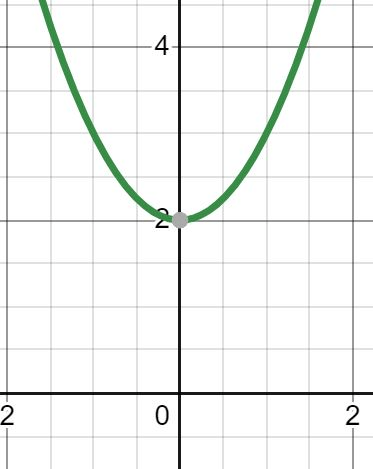
(x+3)(x-2)
x = -3 and 2
f(x) = (x-5)2 -7
(5, -7)
x2-3x-4
(x-4)(x+1)
(x+3)(x-3)
x2-9
If the radicand b2-4ac is zero, there are this many zeros
one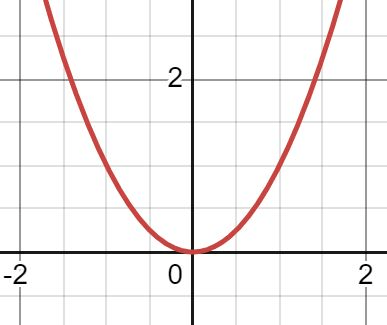
How many real solutions does this function have?
x2-6x+5
b2 - 4ac is POSITIVE: TWO solutions
f(x) = -2(x+3)2 + 4
(-3, 4)
x2-49
(x-7)(x+7)
(x+6)(x-6)
x2 - 36
if the radicand is positive, there are this many zeros
two
x2 +4x+20
b2 - 4ac is NEGATIVE:
NO real solutions
f(x) = -0.25(x-3)2 + 2
(3, 2)
x2-9
(x+3)(x-3)
(x-4)(x+4)
x2-16
If the radicand is negative, there are this many zeros
none
x2+4x+4
b2 - 4ac is ZERO: ONE real solution