Solving for Solving's Sake
Factor T. Rex
Fill in the Blank
Graphing in the dark
Just for Graphs
But Mr. Yurgens!
100
The solutions to:
x^2 +13x - 68 = 0
x = -17,4
100
Factor the expression
15x^2 + 8x-16
(5x-4)(3x+4)
100
The axis that this function's vertex crosses.
f(x) = x^2 + 35
The y-axis
100
If the solutions to a quadratic equation are, the graph of the same function has a vertex at what x-coordinate?
-7 pm sqrt(34)
x=-7
100
What is the vertex of the function:
f(x) = 3(x-5)^2 + 4
(5,4)
100
How many times the graph of f(x) touches the x-axis
f(x)=x^2 - 24x + 144
One
200
The solutions to
2x^2 - 32x + 128 = 0
x = -8
200
the factored form of
9x^2 - 150x + 225
3(3x-5)(x-15)
200
This function has a vertex at (-6,64) and passes through (2,0)
f(x) = -(x+6)^2+64
or
f(x) = -(x-2)(x+14)
200
If the x-intercepts of a quadratic function are (-5,0) and (11,0), this is the x-coordinate of the vertex.
x= 3
200
These are the x-intercepts of the graph of:
f(x) = x^2 -3x + 2
x = 1, 2
200
These positive values of k make the expression:
x^2 + kx + 225
factorable
k = 30, 34,78, 226
400
The solutions to:
(x+7)(x+6) = 30
x=-1,-12
400
this is factored form of
3x^2+54x-120
3(x+20)(x-2)
400
The function graphed here has the form. What is the value of a?
f(x) = a(x-50)(x+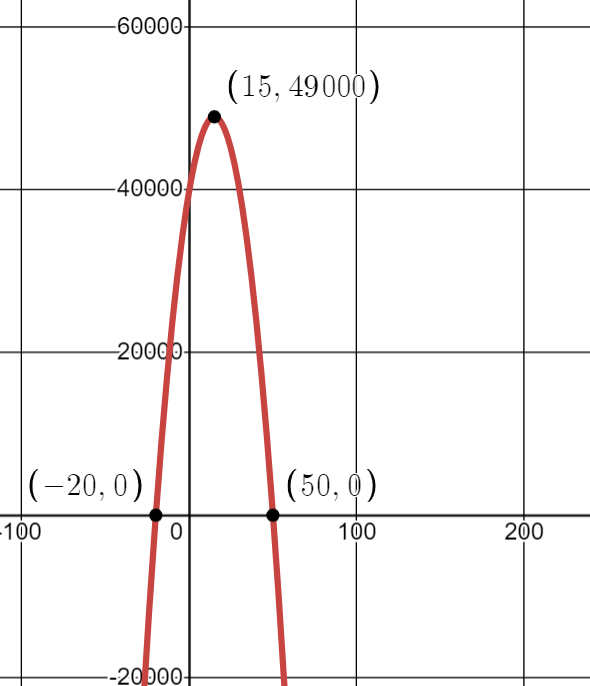
20)
-40
400
This is the function of a graph with vertex at (2,-9) and x-intercept at (5,0)
f(x) = (x-2)^2 - 9
400
If f(a) = -4 on other half of the quadratic graph, what is a?
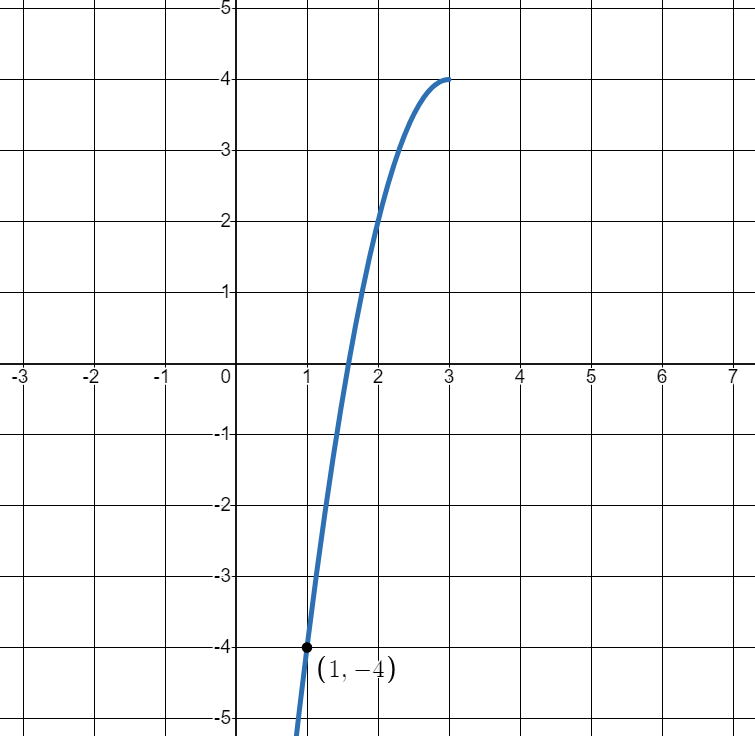
a = 5
400
We can multiply this expression into:
64x^2 - 81
(8x-9)(8x+9)
800
The solutions to:
(x+5)(x^2-5x+25)=0
x = -5, (5 \pm 5i sqrt(3))/2
800
The factored form of
26x^2-10x-8
2(13x+8)(x-1)
800
The fully factored form of the function graphed below:
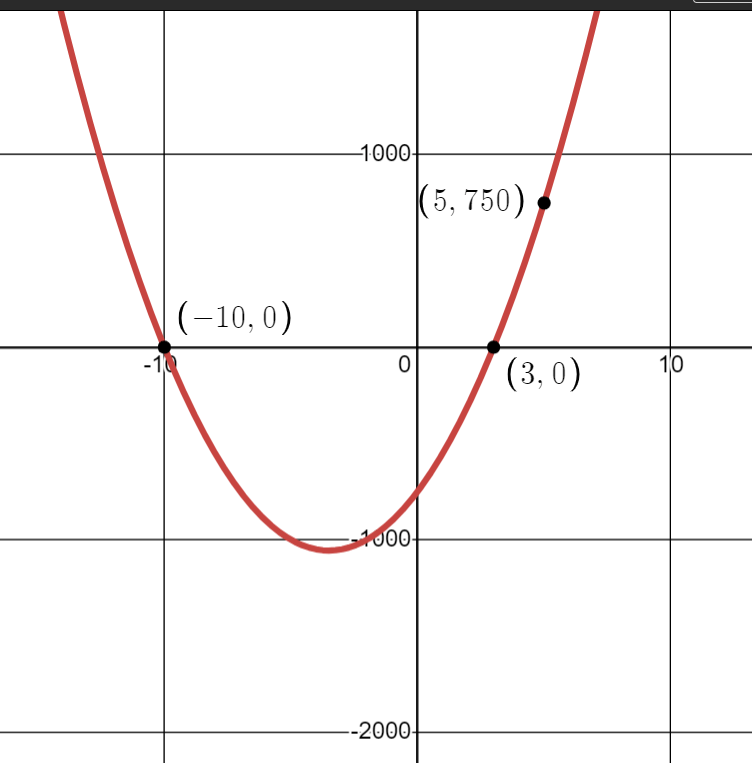
25(x+10)(x-3)
800
If a quadratic function has one x-intercept at (-3,0), this is the ordered pair of its vertex.
(-3,0)
800
The ordered pair of the vertex of
f(x) = 2x^2 + 16x + 42
(-4,10)
800
The solutions to:
(x^2 +7x+10)(x^2 -4) = 0
x=-5,-2,2
1600
The solutions to:
(x-4)(x+5)(x-6)=0
x=-5,4,6
1600
The factored form of:
30x^2 +7x -4
(2x+1)(15x-4)
1600
A function has a vertex on the line x = 8. If it passes through (0,25) what other point is it guaranteed to pass through?
(16,25)
1600
What is the x-intercept of a function whose vertex is (-3,4) and has a x-intercept at (-1,0).
(0,-5)
1600
The number of times that the graph crosses the x-axis:
f(x) = 4x^2 +28x + 49
One
1600
The fully multiplied form of:
(2x+5)^2(2x-5)^2
16x^4-200x^2+625