Which of these is NOT a way to produce heat energy?
A. burning
B. melting
C. mixing
D. rubbing
B. Melting
Carmen is building a snowman outsider with her coat on. What might the temperature be outside?
A. 90°F
B. 85°F
C. 75°F
D. 28°F
D. 28°F
Grace and Tyler were outside on a sunny day. Grace wore a white shirt and Tyler wore a black shirt. Why did Tyler feel hotter than Grace?
A. He was sitting far away from Grace.
B. Dark colors take in the Sun's energy.
C. He was sitting closer to the ground than Grace.
D. Dark colors push away the Sun's energy.
B. Dark colors take in the Sun's energy.
Which of the following is NOT a test to help classify a mineral?
A. Luster test
B. Weight test
C.Hardness test
D. Streak test
B. Weight test
What is Moh’s Hardness scale used to figure out?
A. the shape of the mineral
B. the color of the mineral's streak
C. which minerals reflect the most light
D. which minerals can scratch other minerals
D. Which minerals can scratch other minerals
Which of the following are sources of heat energy?
A. Friction, wood, sunlight
B. Wood, hand lens, burning
C.Wood, hand lens, sun light
D. Sun light, friction, burning
D. Sun light, friction, burning
A cup of ice water with a thermometer in it is left on a park bench in the sunshine. Which best describes what will happen over time?
A. The ice will melt, causing the thermometer's temperature reading to go up.
B. The ice will melt, causing the thermometer's temperature reading to go down.
C. The ice will melt, causing the thermometer's temperature reading to stay the same.
D. The ice will melt, causing the thermometer's temperature reading to reach freezing.
B. The ice will melt, causing the thermometers temperature reading to go down
Kayla wants to build something that will keep her plants warm in December. Which material should she use?
A. white foam
B. dark colored foam
C. plastic wrap
D. clear glass
B. dark colored foam
A scientist has a sample that is made of a single material. The sample is most likely
A. an element.
B. a mineral.
C. a rock.
D. a crystal.
B. a mineral
Using the table, which of the following has a metallic luster, streaks brown, and can scratch Sphalerite?
A. Wurtzite B. Pyrargyrite
C. Manganite
D. Boulangerite
C. Manganite
At home, Sally touches a warm object. She wonders, “Is this object warm because of friction?”
Which question would help her understand whether it was caused by friction?
A.Was the object inside a refrigerator?
B.Had the object been in the garage?
C. Was the object near an oven?
D. Had the object been rubbing against another object?
D. Had the object been rubbing against another object?
The table shows the temperatures taken during different times of the day.
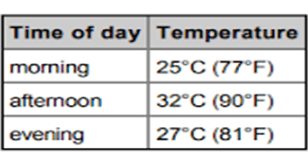
Which of the following best puts the times of day in the correct order from hottest to coldest?
A. morning, afternoon, evening
B. afternoon, morning, evening
C. afternoon, evening, morning
D. evening, morning, afternoon
C. Afternoon, evening, morning
Ron pours hot cocoa into an insulated travel jug. The cocoa is still hot two hours later. Which best describes why the cocoa is still hot?
A.The insulation stops the movement of heat.
B.The insulation slows down the movement of heat.
C. The insulation slows down the movement of cold.
D. The insulation stops the movement of cold.
B.The insulation slows down the movement of heat.
Pick the correct difference between a rock and a mineral.
A. A rock can be made up of minerals, but minerals cannot be made up of a rock.
B. A mineral can be made up of rocks, but rocks cannot be made up of minerals.
C. A rock always has the same shape, while minerals may be different in shape.
D. A mineral always has the same shape, while a rock may be different in shape.
A. A rock can be made up of minerals, but minerals cannot be made up of a rock.
The students in Mr. Rowe’s third grade class are observing and classifying minerals. One group has decided they want to group their minerals by luster. Which question will best help the students classify the minerals?
A. What color is each mineral?
B. Can the mineral be scratched?
C. What does the mineral feel like?
D. Is the mineral metallic?
D. Is the mineral metallic?
Janet left her jacket outside for recess. She went to get it later, and it felt warm. She wants to identify the source of heat energy that warmed the jacket. What question could she ask?
A.What season is it?
B.Was the jacket sitting in the sun?
C. How much did the jacket cost?
D. Is the jacket a soft fuzzy material?
B.Was the jacket sitting in the sun?
The picture shows the four temperatures of a glass of water that was placed in a freezer. The temperatures were recorded after 10 minutes, 20 minutes, 30 minutes, and 60 minutes.
<img data-fr-image-pasted="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAd4AAADtCAYAAAARBxR0AAAgAElEQVR4Aey9B5xdV3Xvv26d3jWaohn1bkm2VYwsYxtcwcTGAVMCLwEMxCQkoaT8U3gJCQEeqS9/UkgAY8dAAtimhbiDC66Sq3rvZUbSSJo+t/4/39/e+86d0ciSy3t/NKMj3bnnnrLPPmutvdbaq+1IPp/Pm9/S6bStWbPG1q9fb2VlZRaLxYzTkUjEotGo9nO5nK7mWPFWaKT44CvcH9niK7z53OX/5yFwDsn/52F8lj/hHImc5Qg8k+7nzcDzq+HXhftezc1n0rdf0GuK5SgyNF7cz6GhIfvBD35gd955p1199dVWVVVVELwlJSW6NJVKGTeOFryczL8GYCL+o8WdObf/CwmBCHrXq8SzVLxzSP6FxOvr1SkYK3zg1ZCImHL+1d37evX/XDtnBoFXzQcQ2hDHqyGQM+vaL+xVTF6TyaQhQ0cI3mw2a3V1dfYrv/Ir9vGPf9yqq6v1EmHGyw8kd9EkecRLvhbBiwo1AXExAn5nw48I3PFVbrr1HJJfJfTOntteCx94LfR19kDo7O/pa8HTa6GPsx1y8XhcE9cRgpeXQqhiZq6oqLDy8nJdhMk5bKcSuuH8ue9xDoHXIHhfF8icE9yvCxjPNXIOAq8JAv9/8oGzkAeMthCfJHhBBqbkIGCZBbMxTQ7+3deEsHM3T2gIvCZNGcidhYNuQiP83Mufg8AoCExEHhAEb5CjJwleTjAd5kI+zHaLbxoFw3M/JzgEoI2gpJ0JKCbioDsTuJy75hwEJgoEJjoPkIwdjWyYaGCmxQw1BFQFIVx8LuyHc6PbPJPfr7WNcD/PGt2P4nNn0pdXc014Js/iA3DH6surafsX7Z4AT76hi/Cuxe89Zp9zREOebKMqhl24LxwLv8eK6Qr94JrR14f7wjfXhmuK7wvnX+13aJe22Q+weLXtnW338c7hvfnGQgYMAqxHvw/XjLWF68P58Husa0cfC/eMPh5+h7bGuo5zYx0P957pd3gG19NeaJfv4nNn2t7ZcN1ouPGewVr6cu+dz51MAwFGxW2GY8WwOPlOd7b4vuLri/dDe2dybfF9YT/cz+/RbXCOY3wX73PtaNnJsZNmvNycyWQKAAwPDQyF8+GhNMgW0o7Cta/qGxPiqaB6Bg2Glz2DS1/RQAjvOla7PBMYBDjwnUgkdCn3BSSMde/ZfKz4fWG0eejAp5y97Huhi4yB4zEOnXTZy1mYgfPptuJrivdPd9+ZnA80wncQPNw33vHP+wY6572H3/f0+BgB11d4+Yh7i36cDq8vd/7lzhU9YszdYjiwD/8M/LLYYjjmzWfhwdHvy2+28D1MB6d4OfA9atCP+unaO8Xtpzp8pjg80+tO9RyOj25jNEwCj+Ta0Yoo154keMPDRjccjoeHcp7GaTQQWfE1E2W/+N0JEw/wGa/vLwKzvEUjDu+MIVwTCN5zm0nwBgYU4PFyYylcczZ/Fwdfns3v8Xr0HQVkPArbYtgEuRm+OXeOBoYhFJRQjozmBeGqUwrecMGpviW143Hr7Oy0ffv22eDQoOVei6ltDPODmLzXpkYzr9G/R/fzVC9cfF1og+/R14djo48X3x/2Eb6kYU2fPr2g3ZzJfeH+s+07Ho0J1/Q7ncnYzt27rOvIURtKpSwSpdjKcBT86HcrHqwjz/ms/JEHC6Zp4Bm1yAhFGbgHOPMd9kc1cdLPgPfiExwLOB99/HTtooCSnzdlyhRramoqzPzCfWM9r/gZZ+N+gBfK5o4dO+zw4cN6Db1z9OXNqwEuY773qLTC4mtH4+dUcC2+h2eE36e6nmvC+4Rrx+zbKQ5yD/hvaGiwxsZGq6ysFB8onvWc4taz87AfK1kmXpGIUf/hwIED1tXVpX3eO4YyfqqNsXqqc+Bi1LlwNXCO6N/whHk0TnXNGPycJsO5Uc0Xfhbzk8JBTxvcW7yF5xYf537wDx+AHrjmVG2+DHSKH+P2eUjoPA2yPfHEE/aVf/mKxRNxq2uod7PfUZ0MLY3sejgKoPnH2dEgP3lKH+4qfmGOhYHDfujny10bzoXri3+f6T4wgOh2795tM2fOtH/4h3/Q4EPjCdaAM23rbLkO2GazObOoC7zr7euz73z3O/bgAw/a5KYmKystLQjlsd4JPBXjzk2UgziGDkZu5PzpaBHxhGtoJ+AdeIffw8OSttzzRj5zpGAoPjfy6S//Kzz76NGjogPy3/mUlpbK3Ei743EmwHvxgf6PHz9ud9xxhz344IPW0tIioeNwdmrYFaHSs1GHMfB6Cm+E8Dy6xYA38DB6C0JPtONPh+uLry2+d6zzxdeOtc/93Hfo0CG7/PLL7f3vf7+DQZEiyPni54zVztl0jPfJwa8Zm5GIHT56xP79jjvs8ccft5raGr1/gL/eK6CnGPEFbh9ODkNgNDrDbcXcIdwVcBbgWwzr4j7QZi43Nh6K7x3uxci98JzRgjTIwZ6eHtHAZZddZp/4xCds8uTJBT5X3KfQ6isSvHQwAIEGssx2du60wcEBu+Hat9uSC863aDxmuazQMmx95CZByoFOLxoYKg1F3ICL+tpVxYCPREKQkr9wlIAebssRgWQ+bfvRz2OZTBe3GYAXAB6AcfpvGDZMxz2LdtD0v/Wtb0n4Dg4OCtgAmnPjkekCyKzlLBZx5USxeGxYv9Ha29vtpne/y2qqayyTzQxz0mKC8f6OAGeoQXjxtCEMFyEK/BRw5HHoKMgRVOFcaBBSKro/HHbNOwZZjPuxrg33jP4e61raYqPM6ve+9z3bv39/QeBynPNj3Te67bPtd2BCvBs0f/DgQZsxY4a95S1vsdbWVstHBfExX4t7CjAp4gHhGBAVjrlOLbhZDoQS8DisWLm2uFfMjStGPTq0S1O0EGZP4Xj4Hos5jvkCow4GGvibv/kb4b+/v3+En3/U5ePiJ6OPAKmoxzOTj6NdR21yU6Ndf/0NsvpI6AVcqGKGZwQe54L7GPh3wzfcGPg2FwZ6cCjmF1eJE4wa8wGnxcAOxwKew2+uKd4vvudM9h0MIrZ//z676667be/evdbX16c2aXcEHIoafEWCV532ko39VDptmBuaWlps4Xnn2YVLl1o8kZRgyuWyw8wXwIhxQvYRmSd0KI9/EAbugBkGXQAE1wTB60edA3XR4NW1QiBvFZDrjJKRSKwwDoUk9f21ANq3LwA64ujqOirGi5mFvvBhMBZrW0XwHhe7KBSxSNQyuaz19vVaf3+fLVx4nl1w4VKrr2+wdDrlzcIaFsOqEmVBJawc+xPu8jmLxZyPWGkGfsy5sQQ8i/AVAa9srt2YVwR1TDdEnOrmbnaw5mQQ2sXHT4MJ94TTXORPw3gefvhn3rfHQadZj2fBK9zxqpGIfPwzZs7U+G9rb7MI9O9hA59AEY/GvAKtW4JC4sYTcHJ04XHlhaTU/DDWC4zXiU/36KgYhycZx0R8n0Q3UIv+uyuGWbfrnFOgfUdP+nolFGAyL46O8eDdGSsFWJ30jLP7gFyLEbNYNKZiS5VVVbZs+XJrbJpsEIDkBWNU2QyuzDAjP8SHaJzAKTwCcVM5nuDh4nHHsYA7h1fOF+HW7Rbd5K8ONFNo58xxeuZXuse2tbXbSy+ts7179ur96DPvL97j++o7qK/TC14vFIGNXkdv7t4Uoas2ozDhvGXzZpmhtGOk+Yjl8jkNQgDNxt98LmuZvDMLMiBzyYQAn4jFNTN1TMt1Ef8BM0yekc8Xa6swNo1gi2j0IM650x8H0/TWJ4zxRR8EhxCBi4BU5/NG9/J5F50sQS9+4JlDxCyTzqjtTHrIMYiIWTKRtGgsMSKYRoBWt5zwHY8DDjgDN94tMEveO53LWSabl883lcka+Mxk8fUkRDfghn/gBaUkkyEIRRRhOcNX5AZwPuuElpRkY7B6wStCdtHT9AFsy5KBIscv4VoU4PeDEHYMgNFPfwOO2Idx0Bf2hXfRmaO9MPDcoGcAORO76M7PZsP741pgi0aZBdBfBAnHoEN653rsWv7F/yvy990cq+cOXv4M1qpYTKbHrOXFBxiTWQ9vmskLidFC9Ltji46G5LaAGUcjUuIdowJkfqbrdgu/4QIOJxxyvIH2wD9jWBSg5wH5qI5Hzccc5PLqg8ObU47hMcQsgKZshomEw6WEAJRLzIKjML0Hb03zPFp9jUVF1UQysxFoGCxd0Np45QEODtA2vBVcOv6azuYMT1SYeDCeGR/w35KShMYfo0Kw4WboB16iNiKWYSwFa6V4NPB2/F2XS5gG2gsCtniE5QvjXzQkZLnzslZmM+7ZHPeb6MnzAPqNXIM3FOOR/kFFknnwHpmtHf8ikyWTQaZFLBaNWzTqxCpW1zBWHO8LTxwjnWj41CvY04Q2Z93dPbZx4xY7cuSI1dfX2cKFC6ypudkNlDyacVTmaV6OF0tnslZSUuqEKEzQE294coEBeC4YQKXvcLKAFJDjA3SCBqRx6YiDAYXAABDh1p7eHtu2bZt1dB6SiXDW7Nm2YMECCYrQB74TyYTugViYodPhoExImHt/TmDq3DMeB1wxTPSOhT+OG4HTXbt327Zt2zXLqa2rtxXLlxsLbLiUIy9cLSdlRpYqX6QFmkB25s0xPgE8IBz4Oj4nBswwCqfogs76wequ5Cx7nsVLKDsNVDjyM2Wu6OjoUHBQd3evVVSU24IFC625eXLh8e45kv6GhlZsRQ3MI9AAOl0+7+htNKzG2+8R9O2VI+CAz3fn7t2G3xshxJiaPm1aIc0ukYhbLuOUXK6Px92YRAlLp7POVO+hD+xBnZejDs9FDFPjmD/iP445j8Q8AXlugxIQoihr4AklKZGIWTqVts3bt8tVlM2mraW1xWbNmuUWiIG5encCrTha8O0V/1B/w/HhEyNg5E6Pq7/Db+peC1RE43H5Ol96aa2Eb0N9o82ePUvmZ5Qr4A/cUUrBPwJMglfcO+eEG5K7ePM45hD3eIHhHQdujHO4sOkaN/ly/MApfyzsQJ8laL2gZ7+7u9vWbdhgHYc6raa21ubMnSs6iNNfj/dCuKifRGZzaUsogMw9GaWPzoXnqS+SQ6Oh5Hp5+hlv4W1Os+M1hMrKCnv00UcUaNHS0ix7d1VVtVZkwCeMZsjygzXVlRaLJ23XseNizE2NDVZeVlYASvHTRhNwYLsCokA5AuyB3epbcNLsm6v9LFY+2IjFk0mLxhO2ect2S2fSVtfQaJu2bLOamlpp4H29fZZOZyydzVppMqEa1vi0+gf6jXebVFfviaC4txN3H56IYnPk8BHbt2+/nX/++bZr1y7V/Ub49nR3O42XqMdYzCoqyiydSolGgPmkhgZLsBSlB2GBZP0g0eEiRuyEoLu6iB+7cRnGJzd5H5Ob6eDzdxYXfqNU4ad/4YWXbO7cudbQMMm6e3usrr7OUkND1t3TZzFmPZGIlZaWSOHq6elW1GJrS4sCqVx3HTWOZM/+RSbKVyQvkzKM7PnnX7C2tinW2tJqu3fvkVKD8nXiRLclEwnhn8hPhHNPT6/GW2PjZKsoLxcPAKsSlp7xDe8XqEJQDbxB0PdEoH3XgOcF0ADKfnB1BIREhH9mWS+uXWvRWNxqJ0223XsPCL+YTocGB1ykLrPZWNwqyivEKwYH+q26psYmNzYaDPrc5iAAnhjrBw/ut66jx2zFijdofOGOItp7aChlg0MDBf8w6wHksznr7e218vIygwakqEvCBqXrZPiG8R6+i+GvYyICGSWcsC3wA9cWSjMf+FBJadLwzROrMXfePGtqabahXUNWkkzqfF9fr+QXto/KikpLJhO6PpUakkJRW1MbXt5Ldt8bHhWYWXEHxyqgMer8Gf3US5iJKOfPn2/btmyR6elnP/uZNMmWllaLx6KGtouJsbe3z5qaJlvblDbbsGGjpu8rli+1Sy6+WEAvzoMKA4uOhH2BrsCMmSYNv6EDq5/iY2qSJpKzWEFzdZBA0yICl6CQHbt3W//AgO3ed8Du+PZ/2qxZs620FKGQtiNHj1pjY4MdP37M5s2ZZ4ePHJZfc9KkSfaed93ESD4jGI37i7xZrbm5WRouCgqfL3/5y9ba2mJTp06TJgx+CD4Qk60oE1PrOHTQZs2cZStXrrTZs2ZJC3ZmIge1gHf98iYfpKvDdWFEudP8dRZIr926uW+xWZnRodlqPmL19fXC9+HDRzXI7n/gATtw8IBddvnl1tnZYcePdxsRi5UsGlJWZvFYTKkT9XX1dsmll9iSxUssEkVZCP0JIy30Lny7dxmvfwVPMzGmpqZma5w02epqG2z16mdty9YttmjhQisrK7cXX3zJWlqbbWhw0BKKB8lZf78LSly5coVdtGy5VVZVS1Bqtllkrh1BB8X8QCDGX5RzNKHf4EM2Lk8Qzj48zKidy4OZNtHYrW3tssB1HumyH/zwxxaLx+zCCy5UsAyzdxg0ggMhncmkxRvmzJ5t17zlapvcUE9vhNqA/fGK55d9L2+1bGpqtdmz59jO2C6N74ceekhjZsmSJZqx7ti5XZajsvIyKTjZdMYGBgaspqbGrrvuOps1a6ZzLbrprcfp8DgquBCHkVlwK3o0FPAhE7bHDBYPyw23A81iaYPXT58+TRbaiopKW7N6tW3ZulUTLfg8Flz6h1xqbW5WuiS8YOvWLXbNNdfaG9/4RsnXV4L7101qAAOImCAKfDoEGvT1DVhDQ2Mh0nPG9BnSgltamhSAMzDQZ7Nmz7Da2ho7euSoiJpZCB8G2UkfP9g4HgCKyZchVvgnc6AbcLyc888E/7DzuTg/nLNHkwaFJktfDx8+ItM3Wlh3T480WgYb5sdcNm9Huo5aNpe3qdOm2Y6dOySAwSnPPrc5CIA7ZjEIXVIsIO7q6hoFYCG8yHGb1Nhgra1NyvvDBTC5ebIUn86ODjWCSUp4DUU6oAVoAtqA0PyAg87CR4JYNONpxwdq4HviM8JfIxrzMQg+OIh+khZ2rOuYNU1ukhmJGIRp06Zqxo7ZvLev3zqPHLGqmhpLlpbZjh27pPk6gSDvowQwL+EcH3J+TCDScHhiPDEmYFjAtKG+wcrKK+X/b5/aZnPnzFUQHjxiz569snwkknFZSY53d4spg+eozw7QeD8VTxAtBF7hcC2vbIEvOB4g/hDoRhySP45VRmLwroj19PZKQOD+mjZ1utxh+K8bJjVqzJOrv337dk0c6uobrHdgwLq6TrhYA992aHMCIb3oVR2flSUpkZRyQo0Hxta0adOcmy+fs/q6OqusqlTqJUruie4TmjliDcVaIrdT4P+M4wLu/QwY92IU7Rp+jhkjr0h6RdOH+7C+8PEjUUYJWcvcpKwgY2jbIpIBWGB6unskB8A1vJ+ZOKv1kaPNsf7BQdu2fZvV1NVYRVWVrLf0N2zDVOUogTmh5oXhAv/9mkzNiJvwIJQTtMFs1iWTw3wHBoY0W+CF8Pmi0cQTMSGgv39AM5uX1r4ozXfOrJkyQYGksDmG5n5JtBWIO1zhnPTDxM5VTgi6QAu3DxMXAMj15J+0aCcwSX1BE6qprrLyslJbv2HQctmsNdTVWl1trQ0ODFhlRblNmuRM4bt377IjRw7b5MYmqygvK/JJDfdpIu8BWz6s5VxZWWUvvvSSYMTMEmKvqqoyIt45j8bLQNu3d68tXXqhNTW74hOq5epQNwxKmDC/vLBVYE34LSr0Nzh9avi+oj2Er8M9gTyBDmjV0ezUqVOVGgMDZqOP9Lur65g1NNQTUmEHD3bYpi1brKWp2VYsX6bBSZtsw15Gfo1+AV0yfv8EGCh+I2clpSVWW1srxsSMERjByBLxmFVXV9nAQL0Ua8z8mzdvEXNbvnSZNdTVOch5BiqAFQSmU5wDDgV3f92wby2owU4YB0xw1AV5OeYd2uA8/CGZLLGqykorryi3joOHrLe3xxobJwn/TNPKykpFZdAEGQyYJpctW2aNkxosBqoV0Bmepl5PzD9KoaFed0TCtaqyWmlWzsrVKJdDNIa1wa39fqjjkHUe6rTU0A7xWGgmHk/qPPw/YFPAlN/QOWrDiJMSXiwXfDwIh0BLGIUEOokGQJVX6OBHoiFfeYsgKYJBq9NDMo8jUOkPpm+UAma8HDt2rMu2bttuBzs7ZXYm7qdYVp0J4l+b4BVg9CZ6KR4OgV511VVismi0mOmYQfIBCHScFwbwW7dus8GhlF100QqbNXOmxV8uDacYuKPeTC8dIB3OKVDHVTtyh3zknSZMHh15TGMV9ubLLlO/8P2tuvgNMimWl5UrmIZUEQC/YP586+w8ZCWJqLVOmWKYxmuqqq3DV+wJj5243wgyF4hGatn8BQulRcKcUMIQuGyasUp+Rqy9faqtX7/O5s2dK3NNY0ODZhlOhIUhA6P0ofkSbg7CDDyHdxdwwdUc4+MsHSMxoWvDPQy0qE81i5jNmTPHpk2boQCgEydO2MDQoKwdmnXFYnbBBRdKKcTt8MILL9r8efNs6QUX2KyZMywRHx68I584gX4FoesZGm6D9rapgic84PiJE1Ji8O3i58UytmjRYrkcMOUhxDBDYu6rKCUQ7/TRwKIJYVthOsMMFrCfic+1iJ+gIF5z1VXi0lhglp6/RIK4rq5WNJ3LUbs+L/8zCjmVus4//wKbOXO61ddiFnd0N4EwPvarMrvzhWwuOP8CuWFisYQC7hBcCDG2rCY7LgJ83tx59uyaNbKELVy4UDNLZEOxYhQe5sa4Rr47VITDcA2hmbKUjDg3rI2PEOT+JtxQuEOvubpBwWGkSB4/fsIqKit8kB2Rzs4sDT2vXr1aQviX3/EOm9rWpqh++huEeOjLy32/JsFboHYGntIonJZZUVEhpsg3JbTokASuj2ClQyCCak8k3Lc0N2mQhqjmwCS5zu17tsoXGhWw9wwW+OY1o2U+YtI+CzDXdbrJddUPyGB4ZrgwcyovL5HiRGpDTfW0wmvpIVXl+gLwJYlWqyq/3GrrquXP5kRh5qWrJsafYvzwxoAZEuA4ZkYrcdolM0wKa4SZJtcizLiOAZpMtllNTbVwjxkHzifjrEcgmBuxySzkBJ0nAZmRdbkIAQ5IR0SMLkpaQmF49kN73Fv8DihWpSUlGlzMbPHveYpzs+yKcsVacx1WEd6nob5eQVfQYvGAGzYuF3o44hXG24/CLMLDFKWavGyXrUBAWqmYV1g8hPcPNMA5/Pps4B+BDBMkP1sDcjSwCscjctUxyYzEnNvJQdvxgPCMmDIe8P06pItOOOkJy/EBJgJmFRWlnvryVlVeoRkbfQmKYujKBYsX2dxZM8XXmNXTFEI5bCfRbDgxjr95e8G2CD/AJrgBk5MbNU5RwJVaFMN87PAGXSDgqquqrdor54CqeHyG3w7KYE1RnIUIYkzRBYuHBKBZPrilxJc8yjF7FojAISQ8h75Bt5ym75iWwWX4cDXPH0xnbOmFFyrWY1Jjo3gAJ8QDRrXtnjD239cmeOmJ47iOaMXk3IOCsEXAEsUM0+rt75fvF5MTdnMGGy/Oh4hnvaTvfAAIkBDAOe6pmhxBaS7e9s/xDADHfBiNWDwSE8N0TngkcwBbaEIH1FECxhG4rh+mSFYRB7nJmawxAyLNhBkbJmf2c9m0ZuwwGd/42NCdSEc9TQe8M+iAHwoXWiLwZR+TE2H4NdXVmlUw4yncE/Dp4SZS8Dh3g8v9AHswRctHxaSdPxVSzIkGEjEYcMSlovDt2zgVOugXm5rM521gcEjtl5QkrbenR4EV1dW1CsZrnhwUSXJVebKjL6jUJao52vJU686f6sHj4DgMT0MzKFT6jfZPyhD5uTGNlYEB8vtjlhpKyW8mV0NZmUy5bqw7WGpEhaHuESeI6iHOX+bw5KrjieX6nGzoiHPuNjCjTF4HZbUZCCFQjOMHTnlyPAVBm8sTADqo/mIyZfaDObG2ts4aGuoUk6JnwTdi+JWH+ck4QOmreoUAAXCptCHVdSBF0MF8KDWkDAZigHqO92jWi5KLHGhvay/MlB0fDngCPxph6hPn5HDyky9GOZiM8XCdc2mqTIb4SPCHpiCMl9kCvXIJOCXVFb6F3MLqSUYGvB/LbYuvx06TxP7wvrpvlKDWUf/Y0U9/TYKXxkKDPCQAzX1H5SfZsGGDOk7tyq1bNitvcqaPYEUAQ8Bs0oJ9x3XA/9FZDzyxR5+czyF8NkHbyfjl+fISum4Qa3BoZqzeKXesuG32dSUO/LwL6tp7cK+tX7/eGidNsr7+ftu0aZNVVVXam9/8JkU/wkzoMkIXpSL0f3S7E+G3UIdZ0Asg8A5cIESInvMoLphm8JXCeDdv2iTiJdVo5swZLjk+SiUsPyv1BOV5rsDoBhy7TpxRslLKF/eQNxtxBRvwzZOkGYkkLEnAhW+kuK2x8KL2NVDNoKONGzfZvv37bcqUVtu6ZYsC/5YsXmSLFy+RAqaBlg/rzkL3UKaiB4ooOIwMvj0Bj/XwcXHM4U74Fw34Mq1SkDK2d98e27JliwQWKXqbN21R6tYFF5yvmraYy8T4NFYdnoO25Ma/k8QBosK399HDgBCwwB+6QAHHXqG+WERFfVyAjWPijmMVWjoZ+uR19vTYhvUbpCDE4wnbvn2b6HrVqlXqN3RMPIsKBCl45ORmJuQRBprGMUG2QolytskYgY/i6yfOZ/+BffKTLl++3JYsXmylJc5/Ds7Y4Kns67dHFfvsukgP9rMq1iJ8wnMMawkFOILQHR6PalVtn3oc0j7zKJ6BoD1w8JB800wacYVs27rNpk+bahdffLE1TZ7sxjTjXlobQZ8EaZ359ioELy/tBBucVR3mpZhpUqdZ/hlTlRJKB+7atdP6+vptz549lsukbWp7uzGTYIZLFSsEJz2mnWC2ZV8b3+yi4QASJWDnLZvBxhS1eN6UcE1/qJrDwGMQwgYZitj70UbVhNe8xgKNm6twZ8SOHjtmL760Vn5JgsIgDiItu3v7rT6V0WIQESqTKPnfRVGO1eZEPCYc+gGjWq6xmIj4hVZO6IwAACAASURBVBdeEOPCwtHc1GSkHPX29GompIAGTIzyDTnzUwF2bhz7n/wAl5QYYvasnwVapGoMs2CEPck9DCAU0TObjDh6c5p61vbv22ePP/G4+kxu74oVK4wgO2brxAQwQjGLjmAQhU57TlH4PXF23FCFYTr4gAyYGEU1nn/hBVkP8OldfPFKGxgcsGNdXVJwo3EfjQztFLGvoDgVDnleAFPI5oPSG/U4poa4qyMOxF2JBscH4AcqgMD9p0CPMxc7giEodP+BQ7Z6zRrJf9JFiPnoOHzUmlv6rKa2WgJAChgCQRroxMHzKd/UiQHxcinB4rlu9SKE7jOrV9vQ0KAtvfACW7x4sVLKCK4saSxRk/CP0WPKiQA3PgM90CxjXTgjm4a7OYaiJxw7axTCrTD+g0x5uc4rr5dCLhkFVxGR/9RTT8klev4FF1giErN+ajvUpiQfEPQJqu+pbVcbQPQVaCx8j/HMVyR4aceBYLgljum4osbMYnE6nrZ0elBpGGiJpJWQRB+xUpszd558utjRKb9FwQT5UXzjxQPPwdNpOmFIIlrdTNe78tQnn1biXXyhd/RVgNdO6Gg4G75BNufy8vG1T5tqV117jb3w4ouWHkq7OtSLF1kSH0DCg4t3PZMAjvCIcfJ9KgYD+AoE55UxBgDCFF/JjTe+3TZt2ixiJpCJykDOnE80oBtE4NfNJEcBS3QBQ+S4QyT4d6qfDjoK0CkGQVC7XI1YtRZuH9V0+CkKi0SkQTPDwYeD3+nJJ5+y2TNn2ooVy6yvp0cmcqqvycyNiSumIe+YhTc1O2oNLY/f78Ag9YYaPwE7Hk1eGJH3PGPGdLv+bW+zNavXKHL4klWr7ER3t6cBN1tgxssmWqIJh+qiA659NRt1UA7X6kaUsuDfK+ZSCAPNinWVpyO/H1iCUiFdyVpUNgpjLF9xkWhs1+5ddt55i2zmjGl27LgrnCKlT3SLKRWlIdDhcLsTcc9hBVjkVTcBJTmVyyiwjpktWSLr1q2T5XDVxauMwhQsHyiBy/ghBigeEx8+CX5hDANrPvng1w2E4u6Aj7ipFr/dOSal2pPi7l2Prpu6Sc0hKChbms1bZXmFzZg+XUG2yjePJ2zRggVKiyPnGPcJtEe6En1xXXIz9JG9OektCgdOL3jpZ1Frmu3yJDYeih/HzzyZZRLQkPcBD1QmmjNnlqIVMUG+8MLz9thjj8i3i+mWKkFsmIaoXgLCchE+DlC0p3ejA+qHA3YGs4BFLEEtTN1Fzh8zXZeTBVQAv0JkBBtHEuqvnujad39ZacdhhndrrK/Tp6KszJ54/AnbuGGdHTrUIS2daFYFgKivwIBB5xucAF+jGQwDxZlYHNz5ncAagH8HIo+QPlRpF154ofI2n3zicdu0eaPBzDA5XfrGSywRpxyn59zipI4BBwVM4PWmbMgAq4bq8oJ4zY9cpjbWDVGQQ6UGGmJRtDsKN8UoC8xbFOJppb2tVZWr+np67cC+A/bwzx6WnxfTKHnIFKN1zMLTkVcE3IBXx/ygd30c9fhf+J/F8DldZ4NCzFuzcAaUwIexjGKNwtra1GItk5ttqG/Q1q1fb489+nO5odqmtNp5ixfJsuBGslmeuABmMxpYvvY1bqDgUvB4zsoKBvPzgg9lWHTirCJS5DxvYXhLu6Zb4pLDb6V3FRE4uxeCnUC7mdPbzfJZO36syzasW2ebN25U5bIVb7jI4kqHQcv3MiAQ0XCz43oP2g8fXhQYigPkwBM+V+duonY/JUFj0RKbPWemxg6Lyuzft98orgT8xBuqaywXdWMK3BdbPhmXEnB+LIMfaIPgqWw0611UjgfAbxjvxPkQcBtowKHHIyngKnx7TAU6cPw8YsRy8Bno67P16zfYY488ZhWV5TZn9hybPmO6ZryK4C6MdBqEN7lPIAA9hsZHPS9wiXDdK/pWZ4vuYBIo8x6slOCKbEbBSjjUCb2HCZ/o6ZaWoxVpdB2rlxA+zlzWb+z4D190kg9Ap//u4y4I592d/pi4rWPdHBl+adDorvEsU7dhFpWJnP7I5Gk2bepUVVA5eOCg6gqX+ZrSrq/Ol6imRwHU9WP8/mWmMzzzdWbFQODyrfHqOTReZoRR1WzOZrI2eXKjzZ031/r6+6y754TV19d6DTNrnAe3YTDzDZqKf/MMh9GA/5N4qIAeBC30EjD9ctjgGg1m+YbZZ9WtrAKpMDFj2di4YaNyzam0hDVHg9ONUNe0pwFHl4EgzuTpL9ezs+Mcb8kmnAnmYMmrIJ5BZ1IZKdaYmSkh+eyaZ21wwKVs4TNwZkkYruxZvkWPwKLxL1bqH8gTJJylhJvFQKJ/Mj1wbLfI1KhOhqYDboZnFfAAajXj/grGLMpBLpg/T2VPKQRBICDLYTLroQUsNE5IOGXRtR7wH541Mb7d6HTqk1N0PDagATNLDWZEI1i7iI3ZsX2HSvNSTpjxL76KKQFXpUd9+C6G4EnHig7oSVgiEMx+fOp04U9xSyP3uRcSItCWdCb6w2fa1Gmaoe8/eEDBlLV1dVIUKa6jiVwxHxjZ5MsyoNPPeEc3VvQ7MODAIAFgoqREOZIsGef8vRFLZTJWVV1t5D1xT0kiqVZSqZSmJDBs1TstAAtIuU1tA5ThQ2KGDp3hqpO/iy4/+eSII25VFEyfhJSr/F8up2i2Sy5ZJY2MtAf6je0fbZfZO+ShsT6irfH9I+B7+C2dlaKY1RRfQ/BJeigjAmRWywIUCF9wCqxdNDHmnZzFcnnlxCpQXEMv0K3DJPiGLYtETkHsxf04c/wz1olsR6FIOzNSPq+I7ObmJrvxxhtVhQuhi8gnUhvNWqEJ8O3ihw4DZsLuAUtMDzLDM+WRHpbVAgjUPr7mmmtUrzeZjKv4ALgH01lzwoxVrRTkIgSOhUV/jK9ipvBqIa52iE5ldS2WL6QhxxMY95hEL7xwqZgxkwVolpk8ka9S6CVYivtZvP9qO3X23ufA6TNMpD+7FYfIhWajHC9leoExEcMM5TSL4/jV4XD1BBeObvDgDIodrOEUw//VAc23j6ySwEX4S6lywbbwgGuuvtouvewy4RyrHnKLPhZS5F4Fyl+T4KWDQeiK4WL+YfZqZqWl5L86RsX4gPEimLmeDlPBhlkJ407L7qmqlPAhjsu7SLhys9eadKzwkq8Px6PfCFICqYo3/AIggoIgBIPBYIMmzHEYMDO6AkEU3zxO93nXYsEqRPGuHicBFpiLmHFQMCHKmsj+PpmUs44pY84Ls1KWEmMmKYbmVrU4Ga6OINzDXiHquZxPgXRG4wdXSSzmcpCLzpG7Td8p3g7T1SqGvi0EtfP10eor7FDRM8bTrnIzGSTe10o1KMYWm5tJuOUgGU8Umi8pobSkgx7MjIBLBFsE37nwPaxeC3eaQTtYe+/Q6wI+aJq+J2OuKH5xo+lMzkrLygrxB5rlip85hS2Mh0D74XdxGxNlPyjF1MV3qXZ5WTdBJoG38NBBUvVyMfFOeG7SoxqsDgwMiudCM5rcBLfRCFoQJYwYy1J+3eEzBzXXjxq2TpiOFIni+1G3QAp0yTsqZoCZNcLa551znfpxhj0Y+ZQzvEmEWqR2hN8u4CgiU8LuPdsUVMWASmcz8unNmDHT6mpqFFa+ZctWhes3NTXZjKntVl1ZXWRMpCMOkppZeL+OujcKWGfY5VNexmuQ8kIAGFW2ACZIb5g0SSaGZEmJbd22Q5GuFMamuk7DpAZd47SkYjPTKR8zrk4EfA+/lFOOcBdwDq2QqOWdu3dZb2+/6AHzEgtkE2jDeaLc9+zeLZy3t7WpGlhZCcrPySMiMDXOiCocaYweN+oO5FG4rmhshePDfS4SxpGIavRSvpAoXNwNLOgxdfo0+aYH+vtVo/fIkaPOZD53nvx9CAne95UMuOLnj7d9iUkGFOVjiQztPGI7d+6UpQgYoXDjI29ra1M6yd69e1V+kZxeUstqa2pkTaAJj2KByIlfd4R9sR4EPNrxK9k8EYS7wjPgW4P9A7Z77147dvy4azFv4lks7kExEJaPJMoVBXHq1Hab0jZFNKK20MAmPBH4CRJKNuMum7Pu3m7rONxpx44dt6FUWvjCtDx12lTBlgpg+/fvtczQkDIdpk2bbuW+eAlIEJ49kvgSrEfRRsDlKyGDwrWBAGg7n7POw0fs0MEOrT7Hb1Yjmzy5SSvRMdHatmWzVl4j/mfevLkKGsPAAw+gd+pvofGX33lVgnd0k+GBrCEdL3UrEN1++212zz33Kun8WF+PXXrxKvud3/odG+gfsNtuvdUe+unPrH9wyCrLSu3mD/6avf36G7QsHGgrANhrPDwPGIXnjH6++10ExdEXjHGqWHiQa/x3f//31tFxWHma3P7Om26y62+4wTauec6++rWv2s7t2+X3W3L++fbrH/2ozZs3R8I3CIXRj5xIv4fB6/ZIEdu5a5f97//3H2znjl0WTyRscCht777pHdb6/vfburUv2b/+27/Ynn37LZfJ2sxp0+y3P/EJu3jlSgll6JiWgK1jum4/EIB7ythDjnOcQR1ycy2HCXfPSKzoOZi60ml75JFH7Pbbb9cFCF4YwJ9+9rOWLCmz27/xDXvggQckJEj4v+GG6+3mm282VjJxK3aO3ZeRTxtfv8ake8V4EFketZ6eE3bvvffaV7/6NcGSdK/JTZPsgx/4oGo1f++7d9ndP7jbWGKxrLTErr3mGvvVX/1VQwljEx8Qk3U0IPzxJyAShcf7kkdAFlR45syl/qe7r5ggRtxktmPnTvvXf/tXe+mldW5lsnTaVq682D784Q9LGbv11m/Yo48+qjXFWYHtPe95j11++WXqO4FeE48ChgEYaCGgRuM2GrGt27bZN7/9bdu0cZPM+BxfdfHF9o53vEMK2Te+cZutXrPa8pmMTWtvs5ve9S57+9vfrkUUZPbHhy4+4J5V/Bwd1+Hw1OH+jLUX8HMqGcLqQ/fdd7/94PvfV8Q9i2OwmMNN77rJLrv0Unvq6aftjm9/y/bv3WdVFZW2YsVy0SulhF2bZ9aP0LfXLHiDxg9QWPoP310yl7P1GzbINwaTYn3DKS1TVAT/mWeesW98/au25PwL7B3vuNH+7StfsbvuvEtL7r3xklUSZhRHYKaL31XOdghbCq77JhDC2X3dsHKi2lcQIbHem4LcDGxYGZUJ1JcSY7aCaQF/HStQUDRj6dJl9ku/dL2Kuc+RLzJqP//5z+1Hd99lt3zsY3bkaJd9+9vfsalt7TZ1aptSIwIgJ8q3w7cjY/aLlX1HAzH5bFhGkRnt0qVLbeXKN4iZkRPLohT33feAPfzAz+yTv/dpO3Bgv/3w+9+3i1autCXnLVaRBVeQwiGR2Qi40uxSC1P7coHQBKaeSE6RraJ+RkBINcFVQIqYtFkoJFTR8VzZ5/1G4lH5bA4ePGg9ff12/fXXa1lDZl9Tp0+1zVu22jdu+3errqywa6+91u6957/tK1/5Z7viiitt0aJFimcI5tSJQgO8Z7HiGt7bmX8jWtcWRrZjx05LJEvsHe/4ZZVYpPYxK31t3LjR7rz7buVFv/td77YffP8u+96d39MSa4wtRa2DSze89ZsKQXBhl0rm3EA8FxzL5C9ly3ECcv5Vs1f+orzFaYjqePCTQrMuMhfrC9u+/fukLFIvGL9uiZYMJXo1Zj/60f323e98T3Q8Y+ZU++Y3vykFfdnyCyV4h5cc9QpiAMg4/Q48INAA3yDLcQXcNs5UjCWRwhksPvK2666T2Zl9LBzf/e53lSN71VVX2nkL5tvnP/fnWrHu8ssvt0kNdfJBoqwFYatneE0Z3CIj9HzqOqOge5+7jgF3b/oVj+A+5AlRxwopcDin7TB2sXStXbvWuo4d0zgn7ZFKVShZZLV87Wtfs8NHj9pVV15pHQcO2t/97d8aq+1xntY8GZ0xxl9GBzx9GwEoXMm+Y5J5G0qnLVpabulcTrObLZs3Kz8L/wiVaxgsc+bOtZUXr7IlSy60gwc6TdHDWXKkopbEn2YxS8SSCnZBQFLUHsEOkWvpQaIQfaAD/iP5kBhfKm5AEXz65JaS0/2sBxwncMP5ZWHkzHQwhbM4c2lphVRlhDCpLlRaomA6if6YyOjrRRddZI2T6o0ZMkVB3PbKNJ3TQ/UX+wrhuYjK2OUT4EoxBBQeGC/E39/XZ0888YR1HDokPxml1w52dlhZQ5MtW7bcli1bYa3t07VKUW9fj+iIPDnh2vvQwV80GpeABf/6HYtZzpf7JDAGWpBihU8ZHGvi5Zkrv83fpxVJnPDlXXAXUBiD6jQUx8AkDi01NTernN3BAwfEEEgluvSySzXQhgZTWjosBIz8YmPs/2LvPCNDWDG2jh07ZuWlJaoAtHbteuvp6VPMBMsFan3ruXNt1SWrbPr06bp+cHBAsAYvcaqZqaKZy/NlzJM6pGh5RcwTCOkKrwhnaVcuNFRrhiYJ2GQRC/nmvDCgbdplo4/QDN/0iXXCCaga9AujUEceYb1121Ytlv7Wt77VVq26xKqqa0TfqaG02hkWOf8XYf0L/SjHEzE3Yz3qH+xXUaJt27ZrYgb8cevV19Xa5ZddrkV1qOk/lEo5BZs0MHi9xr3j1/AXZqGMf/DKOeQNghZ+QyYCwa+YhDH7i08wzGPkBns5wMIonv9znnsJ7IIGqESG8IX3sFHoo6a2Vq4lJgvbtu2wtrZ2e9vb3mZvWHmRVVaWWzoD/p2rEdku/eMM8fKaZ7zDz4HJASQ6nbJYOmWJCMUGYvbN2//dVj/9jH36935f665Goyz7lFeqUSqdLgCcFAP8gh1HOgVAcgCj1CXxgVcpNJZEwtpmz7T6qhppL2jHYQNxBzo6rKuj0+L5nMXFWMmrAj6uzCAz8smNk1WqDrMhyAL4A/198uPcd//99qUv/S/7tQ9+0N563ds08BisIJT2CRogclMIfhWaTujreP2WhulTsoA7K32QJP+lL35Bpqfr3nadm6FGmWkOOeYHbjIsKZmV/x/fH8n1UDKwd3ZCVwIyTUH72lpraWXBigpp2VriD0FreeWHbtm124Z6elVVBurQbNlXVGOQlpVVaDWS5mZKv0Wtn+Ur+/pty6aNVl5RYT/96U+t58Qx+5u//3v5e2hXStqQYwzgLqN63Y72hilwvGL1zN8LIaRCKGZ2tOuE7T1w2GbNPmGbN2+1u+680z7zPz9jZWXlogGYcjpF3XO4lptFowjv2bfXDh7ulHUEYyNhmHxglLlo3tKRiNW3tlhTa4slFQKdUzYCtEIw1MH9e6z7yBGzVEquC02J/SswG6YdeAC+Rgp8QHf9/UO2dcsOO3a0S7WZn3vuWZWH/M3f/C0F3cFUB4cGbGioXEqghL6P2g7ukDOH0vi9EhxICJGlkEhYsqTUjh/vlmL74x9+355+8nH7wIduFg4QpplMWnWbgQj3wVePn+hWiUYUYhQtNmiKcSYaIFirqtKaWlutrpZ6/1FX698H9jHT3kW8xolui4gXORmAgOU3ijWBXSzg0tjUpIkc01ZWylu/bp23hOblm/6Nj/+GsdpWnMwWy2uiRh1nuA10A+16Wf2KkPo6Cl4365XkjZjd8rHfUOfQGqkCdM8999hjjz1uTU2NlL6wCKtPh8AURT66aT+CMZ5IWjxBhHmW1Q/0ciqskUebceUaAYK024hbYxUgiFF7DAJcRjPoQuONJphF5xWdyjPQuiASBhDmgs997i+02PXho132mZ277ZFHf25Tp02XxoZmlYbRSqUB0GjfjiBeEbTH5cWjxA4RwtGYzZs7x/7g93/fWlvbNFi2bt1qmzdvLqQTgRdgKCYtAeu0UnCCNkvUq9eXXHBWlvKihEC6ARhAKTqQxkqd5axbKEMjFPpxBe+Js08m3OLsDFzaVo6xlqg05Zdfc+21tnzFCmubMsVQvv75K/9mjz/+hAY2hdGlbKXT0ozpGP0UJxC9hd5M7G+NJxSdfF4Wow/f/GuqQkQVoIce+ql86NS8nYI5OZ+3RDLhTH2AEl4g5ci5q4gLYJyhV+czbuaE0qtsJelivngLMxfvigjlAgNKlBVMm3mK5Lh23fzEVPrVzaKiFs/F5Xv8q7/+kjVObrT6unr7s89+1p574UXbvnOnLF/xhKtsxbvBi5x50/EAsYWJjXq9PePZo0aTnTlz59gnfue3rK6u3mbMmGW7t2+zTRs32OGODilcwB9eHGaZZIswqKhmSCYBQtlBGOU546xaZBNQntgHNjpcOx4EDXkNTtk1mUzOEHAchzbgNaqUFcu70r/i4U4Rw9Lxvve91978psu1TOj6Devt93/vd+2ZZ1YrwIr+aOU1BY+6GZdTMEMPxZrOmApeJ8HrIrrESCNmx7qO2XPPvWjVNdU2tX2qtU9t12Ds6e2xpsmNzBecUNXygDkrLy0z8vpKy0pVTnD6rJmqOgWzO3yoU0hi9pQhECYaVZF9GLBDNMhGoFK1JG4kOFeXVcivk0sNCRGV1dUKhEkqatYjAkbukULUHRGNs+fMttmzZtnkpmbr6T5hg4MpmTeCMHCAB4FOaJ8xlMfJhY6wvdDxsHOzUV7QKU6xWMRS6ZRt2brFnnjyaXvTm95ks2bNUIT40a5jlkqlZUbOp4eCWiTmy4CgilV9fZ2WCmRAgh9M+tRzZSYEDWQxG5GGUFKiIB6JYS8EEcyUIqUWdGwSKU05layjDB0LrFeUlUsvREvlFuXumln/QJ9qijNQlyxZrMhr6JQo5prq2oKy5gQF9Ia5Mi4N3aF2lPIxTvD9cq8hxeOkC5wwZMELFpJ/6qlnVDJ0wfwFNmlSvXx7jGkYFkxXOPWgC8cSyaRNnz7D2pXrSX5txgZ6+/VJZTMy7KUwI1ey9Kgby9AeyjFmP3hCbU2t1ZRXqKhGPpthGqXytTW1NUaeqK5UrrbLLaVPHZ2HbP+BAzZvwQKbPXumNTW32MbN22xgcFBVkmKJhJR0gk+k8pN3GiQuDU60jXce8d7+h3c3sNj9gYMH7eePP2Er3/AGBaohD6Q8e3Mv/ARLkksjczwcN0VlZYUtXLigAFHKNuICZJ3sbDprWSpUJeMa6861gCvKhTnCm8vKy8XDrX6SsXAj1ikKn1VXVrl1tn3L+ImxhuHCYOK2Y/t26+8fsLde91a5RqsqK92MPIeFM633ZVIg8a6CO7iw3CYZXujx6XdeJ8HrbO0QMB1hHd77779HpcGOHum0e++5z6rKy+2i5cutvKLcYqUltn7jJqt75BHbsP4FW3nRSmtrb5eGSxsi6IL/JitbOi+bRvtNxi2LJpRMOpMlx1Q+DjZLEnzWsumUm5lkWUGGhOe0lZRmLcoCzGhlsj2HWUvO9u7dY//0j/9o27dutdlz59r6jRtt+dKlNm3aVOvsPCQG8dyzz1lX1zEFjFGBp7yiTNANwuj0oD77rxib2XrOqVmre0eIE3/Z3T/8ge3YsV0D75mnnrDlF600ViU63tVl/ceO2GOP/dw6Ow7ZgX17rXFSg4La4GUwZVWGIYgCE//QkMv1jkcsQ0k6VofJZKwk6gueMMtGkOZNqWvMfNOYGcWK8f9mLTWYtmScpelC7rVj/lg50+mcvfD8C/bjH/3E9u3dY52dnXak46DNmT1biiBMffPmLfbUU0/btm3blPiPTyqRDMMnDL8iZuTBUhiZZz/6x3yDQP8aV94S4JhQxDZsWG/PPPO0HT1yxLZt32Fbt+60t99wgy1adJ61tEyxtes22kMPPWRYQzD9EdAEfmQJY0YDTnM5G0oN2cDQgLN8xSKGZy0KM8WqBeKVYuR8wPAO8J1Lp+VCYlF0ZrwI0NJUmZim6Bg6gxZAUN5US/5b3/qW4jcuu/wy27JpvSUsa42NkzXmHxh8QPTa3DJZcSrU80U5nIibcA3kQBDgF63DiB1PxYDJuEJh/tnPHrbnnn/Bjh7t0gpVFM2orKoWv//pww/bf9/z37Znz05llLRPnSbzNDBFKYaOUHMY6/AAFDUC6UikzSFJeR4fugBf54ZMRryfVcYi2azWz0Uu0Bj3Z/HraxlJp6ShqHEOlwezW8b4YGpI/OfY8R6LxRJKK5rS0mIH9u2z++9/wA7s3y/TOaZ0PVOTkFdGCa8b5TgCdgZgApB+82MftX+/41t2261fl+nxAx/8gL3pskvFVH/v05+yW2+93e647VY7b8ECe+/732tzFszX7JKBTPk3DSqAykxIjDVqCYJoIlErieD7dUxOVmp8BdwTicp8FccGz+pHLLjM4OJbq1hALI5Q8pq1ukWPFy5YYNdcfZU99NCDdu9999qsaTPsPe+80ZYtvcDKy0vthWefte/9539qnc6rr7rGrrrqikLa0SsD99l/Nfjhg3AEqA6cELaLMmTAke9MIfwPf+AD9tV//Yqtefopm79wod30zl+2pecvttrqSjt6tMPu/M63pTwR8Xj55ZdadVWFk1NEJLvRLNzFknEj+hhtmbqteRienu1LU6LVEvXOIMWNUJKU34d1Op0y6PrrLDJuxuLIh8j2qE1pbbarrrjCNqxdJ5rk3a69+mq77I2XKO/0uuuuk3/ytm98XTOmD37wQ1oiDP+Tk6/ur7AbbJkB1Zwqksvh8Hj6DsIXnKh8TjZjzS1N9rHfuEV+WlJKMqlBu/qqq+2aa69RlOsHP/g/7NZbb7N/v/0b1tA4yT56yy02c9YMzTQcjVG71wVTRligPJFUwAxKUCxLjV5XXJ8ZDoF48AOYIEVbcsmkYb2gnm9M0tuvgiYx65DBX8Quz8KScflll9mGjRvsxz/+sT368E8VWPehmz9kl6x8gx2bN8c2rVtv991/n9LHKPh/3VuuUaS74gcQ7h6hBViMJwSPfhdoGjrnpf2LC2caDa4SHb8vvGCJfeTmD9gdt99hn/+LP1fA4s0f/rCtXLHCUucvsa4jh+37d99tj/7sIUWMf/jDN9vkxgYxaOeudeur40QlsCqeKBEPyCJfKSXqpQAAIABJREFUFTwprEsBYJUgsJCLm8WyGYsl3FKjWDi0ZGzeuaqEd3iIlATzLsO81dbW2vvf9yt28OAB+/I//G/R0sqL32Dv/OUbjcDK9733vfalL35R8gycf/TXbzEisIPgHQZGEVBGw63o9+siePUocq6YXaJR5HKK/lp64VLNHkpKk9beNtXq6usVWXzzB/+HXX7pKuvv71OaAWadsopKCc8oBei9NprOpqwv3W993X0Wz+HvwcyYsER5meVLsTQ68wKDnSArgqSG+vosdaJX2k4mn7FIPGZ1iZhVaabjlxBDCou5w5gjNm/+XPvsZz9rH/3oRxX8NWlSgzQy1gt+w0XL7Qtf/Lwd7uyUVt7S0mKtLS3O9+TZbhE8J9SuG3MQMYLX4QMAgP8pra12y0c/aldeeaVmLKzH3NLcYhVlpbb4vIX2J3/yJ/b+971fPhcKKkxunOTUZIYPzJWAtmxWZuve/j4bGsRtELdsPGLxSlwTrspQHIUKZVvKgHt2d3+vpfsGtYgG/r9kImY1VVV+tusUL/oumZjPG4U7rrziTXbewvmKboXhE3hBcRdMXx/79V9XOkRvD4thV8gUijlMgRU++IP3PrMhNz5JBAYk1w8zzmxOcFt18UqbNXOGdR4+DGKsZUqrgtq49i1vvcaWnL/Iuo4eNUpJkmZSUV5umVxayhhBT0CU4jupdEbBb0PZjIQpynQUYZxzwtMPZ82UNUMeGFRwXo5ShMycsjmrqqqQe0DuIqFgWFmiP/ihf/fTn7b3vvvdMmtWVVUZ64bXVNdIGPzpn37Gbv7Qr8nk2DpliugDgS28F8UdDDPi8Ynn4bdyo9/9HqZ8hgPjIptL26SGSfaum26yN15yiQqTVFZWWfvUqYIpU+JPffKT9u6bblIEcXPTZGttbZZii3sBhUqWTNbYTWeMpRpZHz0DryeiuTRpsZISw4bBM+EXsohqcY6srk33DVgUBQzeEItaaSJpZF1IAdfMbfhtSpJJCf+//7u/VTEl6KiluVl4Likts+ve+lYjZ/f48RPiI/PmzVPtbvKNZaUpgGMYFrQeDg9Tm3vm6yJ4NZ30DDcad2kATMNnz54lcx2P4sEuVSMrk+KF55+vHnBckYahWLq0UswMTHNZepVZDJqps1/kLGNllrMYARMwaSKpCZjJmcUVTIM5kpm3N0HjR8gSLp6zXCwvBIF0/uHKR1UuKSlTNR0EQNgwT2DWKCst1azcFjifA6YsBXPgq9Ji76NBGlqYWN+O4bjZsFsAw+RvX7liuZRjoKQAOARhMmFTWlqtraW1ACS5GFC6mIXggw1RjITQKfnOmQbTwhwBc85knKfGsnDtgvBoUDjiqIrYE2TlgnPCw+jrMIN0+COFrLa2xszmhcskQBg6kydP0qdwQjtOaw5uvpHnJtavAE8EILyAL5gdMRXU5Z0Z/LVYJNL4yqJK3Zo/d24BUI4+cAV5V4CUKReBCt0ocE6YdrNUHgIz5TmYJYc5HC15/Mo6g+vKMV89TJ0rPFZ0EBgzCjWf4o1nQ6/Tp0/VJ5zjHhRMWX7CwXPfgoD8rd6dp9TMunphjpPyq6o2c0SBts1NxPy4TfxBJASORUpaISrUUAbmsnSJxgLOHc9RPQHPaeAdfMTckS6iJeQBc2IRqZdIPNdJYHCJ62D27Nn6hD7BXThH7vGFFziZxTksezKHewGuZxSIMNx96u/XR/A63qVBEwKQAFI6RY6UY6bqApoJmgyCUEByAllvYVmTPwZhxsVitlkN3lIJVwYZeVkxi1M7GS0TaEcjVgKPJdotH7F8LGmRsnIJ1TjPiFE3usz5YyAGGsePDPwDk5Ym7ZDNaRDAs5TioqvI93S1mXk/GA3n2YYZuPs9Uf9qUCjAyuXGAh8013TWzVzlW/V1TUn/yeVZPMFxwUjORzf7vFpwJCMSkaixhFWUV1o6gciNKkUoWpb08QDOvaBngeuIMymXlmAOiZnimCmU4uuDB1y5vjrhAL6koWdZIAGmP4xB2lWMQJq0AalpimzkGG3Qnlwd/haR1ihNeri18bsX4Cm8Kd7CMUPgI6HJ+CLtgnEM7MC/dyZ4/uyUK6creaYAvJwfHsGHpUEKtVx7rt67WCiBWpgYlcftYkywUmARiRIxC9OlEhmBdcLbsIwuYATTJW4sasmTQxr3wZPcS9oIq+fkXM4uF8DDoGfwjZJXRDKFJifSjvAQgqp84JSwovHMhCstbEMPCmy0vPK0sxlvKQuuYs9Ug7fG8QCHazILwAtxzpiaLUGdB5fbr9xcBCQ4FFYilownLFFhFs+6OAHy+omUHyl8h7EUaJVgL1luQr1o747I58nvd2lE4N7xCi9P1H8n0odbfPm910XwujmHj/bNR+XXYbEEOheLUigfAh6eIYhhweF8h9GCmPeK6SFMRckuQpJE+gS2ROa3ZAwRUIPvh7QT8vsQxgxqv1IfgjmWTCrVKMqsVGYpZ/+nXXCr2ZLgkpO5iv4EJgvLZ5/hRP9FCzJlEDnnItoAMfc4Jj3Rh93JBOYYsUsPAfmYekErQVEkv6MtYtEAvoyTcH0IegOwYsgwNUXAxiwehwZg3A43IhkYNf57GiyqWEadZdqNc5yUBXAlDRifLO24DRw65o4iQH/ol8c5T+NZ8mU5WtBsTBeF+x09hfYm+rczDXqFxC8JqZErs6ETxmHMAysYJhtRrTou2DsFJ+CGsYbApuABSGWtVeiD8whb0ClWwh+PKynnCF1mpHQA/uCfNSaOaEP4dvTgxjw4d0oCRKeCLP65asvzLu4spqkx2x93BwEqn8D7wm/3osKZkluxRrjKUvBOtrgyAsGpC4xi3NFOAYdFsHJKGRf64hl+8QyMoQRI8Xj3ZDAgrqy7wRs+YYsj4HFFIVNcUKYYi7od+j78QGgK3IZvx2wcPfMcFDoe6q5xY99V13I0ONzS6fdeF8Er/sWzQuANgIpTeeTkGQSXFa73/YtT7cgSytVipGiIMbDSaRvs7bee/kEtCUfMFIK8PFlqiXjSkgRWMK6IckuYDeVydiI1pPqvuaxb7QbtlIFbWVbhcrnE1N0zNLjFyR0SiscmiMyh2Z4ChqKXU5ybkIcFQmksYlgSkhAyrgcA4gGJLGQwFAYt9+FKAN6KZHRMlSuy+PdSKevu6bbUoEs/SsciVlJVoQpDDDD+EeQUp7JVnjU0MyrakekbtCgPI1k+FrPqqkppuwWG4YkwMFnM4xySfPYIZLDh60mqw05I+FOiRzfbce8cjhfkehjX4btwwfjaYQxpHHmMMluQoJIkdfAk+ClswJRZTyiMwHFSddjERCVIAZpTgHIZF5FMUYSUZ+IozjV1EcULCI1+1ouCNZhOWXpoSH7aLIX5fdnZ6spKq6muKoiK0J/wYNGRliRkr2iDtuRvPpkThJkZ/Q5b8X44Nj6/ha3hcSzsuQkU9gyUacYn+c8oWMXQc/NGMFxgCyNAxL20Dl1BK2nxgB7r7et3pmqEaVmpxRJxK48n0b6lWKPYK6AyN6RI9FRvP2kOyumFD0GHtVVVRX0ueiyCWRYSV18gnIEvwSOIJRm9aQUmKWCjz5z+9+sieJ0QchoiMxmAhXaQSg3a+vUbbfXqZ62tbYpddtnlKjK+ceMmlRHs7j5h7e1ttmz5Cps5c6bFS0hSdzNjZj+JaMTK42WWLYlbPhY3ipEzqBmoaBoS9ISJR/PWR45vImL50oQlcmUWz5cpF5jhXBIjd497IzJxK6E+DHA/C2bmRC1mQso7OzrswmVLbe78+QoOe/rpp23Tho1WWV5u5y1aqDKHqic6NgpPD/XxeIVmDcOaq0xK0aiqvzxEJaiebluyaLHqG5Nm8MyaNfbiurXSTBctWGDLly5TNTFFmirPFqHNmq2lVkbyOvmX0ZgNUZGMNZ8pGanUEfL/HEAVFhCLW5ICLGVmSUMYE6wHTXnzMAKeibAb2hpUErhwgXzeXnxpvb3w4kvyQV566RuN+sKr1zxrzz//vB3q6LC62npbtepiW7x4kVanYTyiu53b3AxAghirBjzA5zxu3rLNnn76KYvHk3bJqoutrX2Kbdq8VWONKmUsML98+XKbPWeWcjiBpVPFHPNNliatoqrKSmSizov5aslJ2ve+NpRmYkWgH0ySmJrNm5qxiGjtVzf5VUfhU46xY2lzs2rooK9/wFavfkZ8i7rNFMNPp1Pq6/PPv6DURHDP8abJTZZIKNKkgP4x+HPh3HjdQdwiKvVPAhelyakgWLhwEfzw3vuUTrTqDRfZeectEoafeuIJe+mlF21gcMjOmz/flq9YZhRccq4+mbOEG36DPwQszgTqs1vS5f1r9hn4sHg5otKVB46QnhZ3MSLgmDoBEuqS6mDD7XAO9wd3ohCyStGDD/1U5wkQbG+farv27LUHHnjQ9u3brzoDl1xyiUEf1HN+NdurErx0lI3v4v0ggCmiwCV79uyzL3/5H+22275h733ve2zZsqUqQv2FL3zB1q5br2CW7du2GukZt/zGx2zqzBkCGgFV6MAISxzYREnmY2ZpOGaMKCpm1DjLKQPpTD0yXUTJ/QPQ+GRgri7wClOWPpqBu8EpMAdfE0I8EjXKxH36U5+0AwcP2Re++EWb0t6uVWn+9E/+2Bobm5UfSHL+7/7up+26t77FrdM7EUdaMaWBaE8Hzpzr6AIaIMr88ccft9+85RY70X3C/uzP/9za29qVlvE//+dnrLGlRQI5O5Syz3/xf9mNN1xvJXH895KMMvMyUMA/bUUjWVWtwcSI305CT6kB0ECYMblgCLTRbD6jiMi4XAZovo7ZciWkRNfdQGRWE7HDR4/brd+4zb7yz/9kC85bYrd942vW09NrX/rSX9tzzz1nkxon2Z5dLPxwgX31a19zgTi04edIE4kUgNvIsS+fgVNktP6qmzl2dHTaHXd8U0XlW1qb7R//6Z8EeFYt+vGP/8tq62rt4P59tmzZMvvLz39eGQayPBFMCZPFd4uPlfz8bIZCdppGK2BOxgbydNnxqYLQgbe8wQRQAEhNzJFm5AM4w+SA/sO4pSQqBTQrBetzn/tL++lDD9otH/u4loTbunWb/dmffdY6DnVohaW77rpTGRDvf9/7rK6OgLwJvmHKLSjeDu+MLaXb5fO29qW19vm/+JytfvpJ+4M/+mMrr6ixXTt32F//1V/b4cOdWg7yzu99V4tpfOyWW1QARzjRqHZBmeBfwbl5/LgEtjrXxYhx74U9sR4iCXBPYJ0sJVhaoCMXF+Sb9jyAcy4Sv6e3177//R/aZz7zx4po/uIXvyhecevXv27f+c73xPOhSyox/vEf/5FSisA+NBfaPBNqeN11dQQaJgYWPH7iySftpXVrxRIpEQnzZF3Lp558wpYuPd9++7d+y2bPnmNPP/OMsT4vQVfOheMFusq8kb+FKQG7RM5i8YglcZTjvyFwJp+xZDZrlVmzskzeKGtRil8YE6cvtE2hdBGBZAQ6sZv1gB0V8s7nbefu3dJojh47puCtbD6rBHAI5MTx4/aBD33Abnj7DXb4yBF75umnZco6EwBPpGsCI+adwWNnR6d9+z/+g2gVF1CTydnRrqP23PPPC34fuflme8+73yNmunXLVuvu7nH+Mi/BNCtRoXtmvglpwix0EYIbwJ9Tsvh2AxGmTUR9aTKpb7RlV34wroA8OqbAPAJ/FJCTt0w+Z0OZrD3+xBNK9q+uq7dESdIGUinbuHmzbdi8yS5YeoF97GMfswsuPF/5nnv27HVFWoLARwBLE5hIGB9+V3DvdTA//3BI3LB+oz340EMqHZlJZ21oMG2bNm22p59ebax1+4nf+W1VKaKc6IkT3WJeUV8Glh/MmoVD5XEmFC9AUA3+djYJVo9HAjkRzmHGA63oQyBOwsVoIGhxK9BmMb1CP/AmZjUI2rr6BlVVYmWaJ598Ulaw97733faRj3xEi2qwUEpKlfE0gR4GxITY8+IOBVkbqqfj2cMwdcotq/385Cc/sR27dlt1XaOUXxZKWbNmjQ2lh+wjH/2ofe4v/0KwfPTRx6ynt094waIlEc6CGYm4UdEMnHEc/EMX8t97YUtgOwFy8ATcHZiVwTm8QMVZSkg/pDylU7acS8S7uGhDcT5527Bxk9133z0qAFRRXiG63btvv93/4E9t5qyZ9od/+If2znf+sj3z9FOawRfQLeIv/DrtzusmeDXw/EuBjpfWrbfVa56zJYvPt9bWKQp24jhmBVIDIGwK3dfWTzJKCXYfPyHNhOFKpzxqxcFVYcavNlIeiVhNLm9VuaiVpvOWGMhaSV/Wyvuz1pDKW20mYmUwAVqgIQnbiOp/lvpAG5QDVblCG4pErbunz+679wFdTM3e6ppaG0ylXTkzFftOqgTZZOV1xu0IpQ9Ji2ALtHdaUE+cC8Bhd0+vPfrYo9Z55LBqoLK2JYOit6/Puo6fsMrGZmtunWLNzRQ6r1eptgF8+ZqhOGuHY67MrNxvGLLoDLBrkgOe3Qo1zIrRWsEHz1dKEgYSv4oJ90lg+xmqqhshuIWWiG3Zut3ue+B+mz5jul3yxjdq8QwCQ453n1AuacOkBhUAwCzKoKWAu56n+x0RFGh2opKFt3xIeTaznbv22d3f/4GVlbJw+AIrLa9WtBoCltWgWlparb19mtXW1ssPmEqlNOYolM8MQmZEBWgSXONcWeTvolzJuiImy7B1bgRw7tHprSEE1cFCHLN1irhTEByVuNkUxwcHB41KSus2bJDra8bMOcI7yhnCA/fWjJkzrb6h0UrLy/XMtOrBOyXTPXii/XXwlrAtCGEHA3DH+MF1t27dei04gbvRpQbmjZWoWCxj1uxZNnfOXEWdgwPuAeZa+MSrcMIv8y5WGgL5IgAv6OH0WC6JnCdFlMhmeIECM90KR9AKfmb65GSJCjc7XiPB7XhDBybmBx6U0F143nlyb7AgAtaznu5epcGysEZzc4t4CfnFmumKH/H0M99esak5PEjALn6OF3Biun399v0f/sh6+wfs6muvteeeW6MkeJYJdA5pZxrkN34ZXg6Gm+oftB07d9n+g/s1cChsTlk+ZzbMS3vtPdFvW9a8ZGXH+60unrSqZImRmXKse9C643lLLGix0lltNlCWsAwRakAjnbEoNqo8xRQS1tTaZM0tzUbSNM996aWX7Mc//om9853vsOkzZtqTT6+xTAqgghCnGYNcquHA24shzPue2xgL0nkFCoieGcHdd91tb1x1icx1EL/EnAKQmW1GLKOVadzKMtA/puDjx3ps584dsjZEEzE3yODkAJ1VoWJRq6yvU+51ecLhjyAqGCzCtLe/3zo6D9vAiROWJOqdYNdsznbt2FkY9CxgTz3nlpZmac8EbTzyyCO2d98BVTB79tln7UjXCWnc+IVIIaN/FHOgCg4kpQ+zbN54ghMBPEEKkYcDitLAwKAxg2Ex9De/6U328COP2f6Dh5wgjLpoV+gE86GYsW8DhXbfvj0y6zLexGRhtLGI3EpKF4lEbMqUNqvEv5bHn+gEL+2ks1ktOXe866hlBgaEQ6UU5XO2iVrPadbkjah2+PTp7ZZMlohmN23ebI/9/AlrbWvXAujbd+2SFYQOx+IJi2KqVnQ2lg0q5UUs4wW9aGAiMwHP+4tBACns2LHLHnzwQdVImDZjuv3gBz9ybkNn13LKEVXnJMBymsWibLN8JGVEe3t6nLUMpVn8A1aekauxpLpKOKHOQtL7aOFBmKT7Bwbs+LFjNniix3JDaVcTAj6QzsAM5L6k1jtFWyiIhDWNGs0P/+xntn/fPruUhe+feUYWGJmgYxFZQembUpao848yF3N056YF3uVRDISX2X/Fgvdl2nL+krzZU08/Y0888aRWfVm3fp11dXXZgf0Hbd3a9WKoJg8upp+o6mAi3EgPQihSEaiuvtaZDCxig/0DliXHMpe3smjM0l0nbO2d/2XlOw7Z7Ioqi1ZVW2bIbOfBLttdFrH2919lc6c0W7yixAYibvFzoqDLyxKKgCboq7y0XI72RKLEdu/dY/fce6+Wo9uxY4cdPnxYsxwYButHooUjNKhSA4IAuJtdeUhMcKY7gh7guGbC92OPPSZNFz95R8chrV+6Z+8+271nj2awZUlnNoKY0UKZdSA8gTHl20gJwotLYfyB1JDlc5gQXfsquKLgGDejjUZdmkmCgB5SiSQO3cwGYY4NmOX+1GaOZQHLtNAGdIfQWL9+vd17zz2q50vd7u07dthQatCeWb1G5i3okn6hqLm0FidsC9Yl2ZhHQGKC/nCzEF5+0+Ytdvttt2sd26NHjxqBlCz1iBm3hDxrLFtUKCPrwKdwYJ1wPKDSUrUpN/PJ561/MGVDlIDFm06kKyZmTXRd2kjUx3kggFGUoCWEIVm5RLkyg+I5FZVlmv2KHsgLjcVliqQO8EMPPawVyd50+WW2p2ePKpgdOnDQEMhE1ZMZQVlCyqG6uJOMzJkTFNFjvDZBaj5wghGYNwWpsVDK/IXzLZ3O2v4DBw0eu3//flk+CZYkEI7oZPDKBu4IpKJymLNWRS3l67UjdDVBVUCdE366D5dkgkVyIpYgPsiXlIVPcJ4xDj0kS0utLJnQDBllivoOPA+9HivMN++4w/bu329XXHm1akt3dHbali2bbUZ6hnVTtzka1ay3pHixHXUIYlQu4hhwGfvQ6yJ4eTkPNwGGhcKnTZsmzfPFF9fa8ePHpTXu3bvPyspLLZUasHRqSAKs68hRKy8t1eIJydKETW1rtba2VrFYHONHOo/IX4y5iNltOldiO6vrraSs16bES2xKNGmZZMT6kiWWqUzatOZWmzl1uvU1VFh/ImLRfNSqS8qtvqLSEiEmXIE3bqKCWYtVM6gTe+DgAWlax44eFXHgi0AhYFEGKu4M9PVrbUmWiEIDO7eFqZ8baIEG8LNR8GDRokVG1CrlNjEt7tu7XwtNJGNR6+48qFVDEHDHj3VZSTJuFWVlqtdcUz1TbgIGS2//oB07fkImKOhsiMFdQpRjqczMCG6yVZgJsV+SKDFcArH6RishLzTrqpXV1FVbZXmZoyvfbUYjGi2onNLWKpfH5i2bbM/uXdbXc0wzL0pHMtPu6+lVShNrRqP1llB+jplY8YRXJvGJQRVieGKwI+d74Ti4mNzcqDG+Zds227t3t/X39du+/QcVDYzg7Dp23AZTg1qXG5iigKHgYoJubZkiQCI0j3X3WHd/v4Qt3kRcVWUVrDTlUo5kdubqnFPgqDKEjx9SIQ6EAhhlyaSRiVASUpfQx5Sk7Whg0qRamzdvth0/ccz27tunsoFl5RXKaqBpypee6Om16po+6+/vFTMPecgTA+Nn9paBK2JJRHhSivPE8W7buWun9R0/YscOH7ETx3pk7SLTgQVJTrRNkam/oqJKY6usNGnz5sxRzAQ8BcWLNXpRvqCvXJSV6ljVrlQ4JrgOXOQ0C41qlbtJDQ1m1TWWyCJ43YIb1VUVVldVXZBVGCyCBZcJ2YKFC20onVVf9x08oCyXA4cOWX1Dg5WVl2gmTTAYqW3wMyZgQRF3NtwwFsL3qWH2ughe17xPIYibvXHVSjt/8XnSVDZv2Wrbt27WotOXXnapZrxz58+z1atX2749u23j+rX2rne/1+bNn+eKIcBA6TfpQSmCMTI2MJQxS0QtwXqrpIdEo1ZCABVzIJWOJHUkYxGqJKWGLDVELl+pZbIRi6vkZMbSuYzFsq4iAsSBb5CFEqgf/OEPfUgrIKF9feub/2E7t2+zi5Yus4suWmFdRw/LD/3Vf/1X6+9Paba8atVK5QSeGqzj+0xgrrylgyVycjiqtKa2zm666V32trf9knV2dtjDDz9su3fttPMXLbbLLrnUBvr77IH777Wvfv3rEsqDfd02ZUqLVVW7pd4QiCiSuBioepNKDSkoh+dmlB+O3ajIvOnpXAU4cAkMpeUqUL5gliI35JqwBJzzE3Cd3gFBGYvYeQsX2J995k80CNdt3Ghf+Zd/tnVr19oVV7xZkcv3//d/27NrnrWOQ522bdsWmz5jhrW2trilAQECij4f8vRPP+bGHXEE5gVMeX1wN2vubPurv/2SpYbSSiekLjuruixfcZEtmD/P1m7caI8/+aT9w5e/bNu2bLbZs2bKCqHlDmRBcJGpWdZhTQ9ZamDAUvj/VcwCAe3WXhYFqhSgm0ETLIm5GlM3dZpZswzzImktXs4K/pqdiXqxsiS1ahLxHZg5f/jDH9iBA/tt/vy5dvXVV9nOnbO1ktLtt9+uus2llMKcPlVrPPO+KAdhmwjoR/lxH0Y9G8INJXR4nXLmmJhsyWTpHxi0W2+91ToOHNDa54sWLlTw6wsvvmD/8s9fMaLdWYR+0ZJFWrtdLXolFlrCFC2cskQjFMYsVTNXN57pBP3AHcj1KHGkgOUHU8aqkLggGOfZMgoruUCwwjP8bKGmpto++clPSShjBf3TP/8LO3jwoF14/hJbvHixXXnF5fbow4/Y5z73BXk/qONNiWHNpvME69Iy2Pd9ElxO/ef1E7xF2gMFyVlgIBaPWlV1lf3WJ35HayG2NDdZe9sU+9Jf/ZXdfdf3bcumDfY7n/ikXX/DDQrd5iVcwArBEC45s39w0I53d1s+ETUrK7NEX58NDaWsUsEXQNz5DkktorQVfp2B7h7rTUZtIO6qW5FOki0rsxzmTGCBqqPVdKLK+WycNEmR05y66sorVJdzyZIlmjm99W2/ZMnSMvvJj35os2Y22A1vv14+K9YORqvjc25zEIDo2TAXNtTXKxiiqWmyZiYVlVU2b85cm9bebu9657tUx/ne+++zuupq+81bft2uvPIKmXVVmhELCnW3WRJuiAIaPUbgFYUTMtGIleYrtbZuLpGT9ouw49kMPIIz0EZJnteKvr6ARl1tpUVgkD6FSIqXk5lWVlYqFwfUwXq+H/nwh+V6WLBwgTVPbrLf/3/+wO6/734tDfhd2p7uAAAgAElEQVTOd95k11//S1oyEinr4rmGaSDsOYbk4DGR/joayGs2UuVrcVN9jgULwOGK5cts+vTp9ke/97v2Xz/5L1vz7LN24403alGV9rY2MU0xUf6wLKDu67fuEydsSKkg+HvjyvGurnIFMWC0YRrDeMR0rOC3tFs6MJJ35WhJQWILikLAC5aL+vp6maHTuaxd95a3WHNTk4rkUxh/wbz5VllWbnff+T0bSA3ar77vfXbFlW+2mpoqVwoxIN0roqHdifPtqB3FK1gfcCNQ+7y+rkbi6JdvvNHaprTZjOnTbPbsGTZ//jyl5911993W099jn/z079pll14qNxPjmJsUF0LsTyqlpRgx+QuD8agly8s0bqVAF8kNboRmWFRlsLvPLJUWX4gmolZeWuJw74VtGKOgL5FIukVRYhGrrKq0T3z843asq8uWLV+uoLpPfepTNrWt3R5//EmbNq3d3v72t9vy5cuEYgndwPzOEOmvn+DlgUrpkGVOM1N82VQMglAh7v+PvfcMs6u8zr/vU+dMlUajUe9doggJA8ZU0cH03ptbjG1c4iT/JE5xHHcncXdsjI0Bg3DBdEQHAQKJIlABiSJQ733KmVPf63c/e0sjgTHOpS+vhg2jM3PKPns/az2rr3uRJyMHQxP9fvvs4xATCpoCKgvObhfPrxCvob7eFYWJTFK9yK9sag/N1FGc3xZMVEDjUGNdnRrJEfZptuLFDqutqQnQkVjL2CWRW8J3QDgEPFYV8f59991PEyft40IgQl9M2bnwggt02kc/GqbcNPXyZxDwvD8Or77P9d7L3xYkEGuCF1AqAG6R1sSJEzV27NjQ3pNKaVD9QF1+6aU67dSPmhYMnKb9C5QirFPOQlSD85BX7d2rl5hsgjHWReY3l3FeiBix/4uUKR8gx0uIq5qrdXEVXg8QB7QU7Uosi3fTg9+gP2kaADOOO+44G1TwE/zxkUM/osn7T3Y4DH4lZBXCVJxypwW9lxP3fd2ehVmUV4urfgcNHKQzTj/NexwBx57cd9+JGjN2lNvKyOmRbwu5+ag1LCqYI89X11CvPlFBE3k89Kyxe6NQP5B0oac/REHqQDWy8Ya3W1G1VFJ9rtaC3Db3u9yJ+0SJnqVT2m/ffTRx4oRIjXJHCR133LEi0oXSbmpqCLleY9iGwr53OWWPfgoDiNoL8PP5ff/99re3G/L4aU+XOvWUU3TkUUe4JZAKZ7eJWREEQ9oMAwBSNqOmpkbXC1SiiXRgObCnkRYAK5GD5/1EyYCLJE1Qm84qE+NAJKVcLakmc+g7aYPuYo53NWFs+BOOP8FGvGV8KmXH8FOf/JSuuvIKtzYhj3gtOIq7iZZ3nv0dz+wxxYuQRFFyW3HuKxQ1JNVYX2/mdazdEz0S6t2rye+l+KXE/MS4cpWgpbVZEOKcyzdocRwBrfP6DiUfrCNywLylijJkQDGb0mHpqATdwiD0eXGViMtwyhA0gd5YLtksiEipED4yeENJuWxGDf1awvWykTkvZ/B1vmNNe+4TgWTeL1irIQNatcLN5UIFMvzB+gEp2tLSJ5T9uwGffEm3bYExhfCN+sI9V9V9nUnPaN6x9hhO5gW+PISagIfjImxfVQMgOxsznD3Epfx5DC+oRbViFSD/YGUzmAEYUvNTZAiw8QFLoLCGKnz4knOE64huvOdSfuede1u5/C1UfQYn00WUFD+FrUu7SEK1uRr/sHqEEsN6BtohS+LDezumHnKGWavAlRFaFMYdPBBkQmA+BHFoITLNmdEaw5vFJ939EezweD9TTJkAcAPFUbF8IgdIK1kQM3RnxLCI8NDOa939tD3v751rAb05MFZwrmIHKzwXxun1cdQgyF6iXezTELLlXeHz8AUAN8DFwiuOW0YFVH5XCHyaJjbYPcQgtBAZXd9R8Bjvm0/sevhb4nA1iiDCZUbvcO3WW+Wy6hvq1CvdaBaDN3C+kAM7efX9y4E9pnhZES7GINheulACjvI1dqejfNxdEI7cHAITi4EEtZFIIkvZrMxiMVnC8zgLnkhRAJOz0OVCB4hhRR/Sfc7ZmlD0cRULKpAXSuDthEkVeFPVbNiQMWvAF5ASD9ibzug1YWqOGSDqJeR74nAWn/VCxy7PrjTs2X9FgiuOJDhUZF50XCLyaIJANIpM5H7gncDAhJiirRZtOoRbWeViUV2ET0AyM2pZcmdejQ84LBUe+TrafqpdBZxdz2LFGIM3Lfi7UcgC0/Ia6zzAD5rOcJNTGLw5gLHzG+eIc4PcasxH3U75wa+uRe+2Nt3XiXQQK2pjSa50xT62kcb7IqxsuCCwEsZPEHC0HbmVy29KKZ3NhbBjRHuEMeflZWQKU2aqTBsC4cw53u5owe8kE1XPVuMwELIMXwoDMZlUJhGGbsT0Np/yXZHUef/i9p3fu7c9E4fxAx12OifsHeSmZadvOihR4CR5jdSfo0dYy7CJreZgumPkQE9SCNYZVnZBoROVsiKOHD/4hWugGK5aLKhUwgtGQZLjDdX0/vruRDPvoaiD0cfngzEVhItN9lTaTE0xLofvIzK8eZf1x18hEfaY4o1FK0zL71gLXGl4DIMMfEPxQnH17s/CM2URKQ/3PflzwToOT9gTSQeixV6R1y0ukrHkJeSTULJSVqLIhguWcfC7djZQB8JQ5RYkAsoXYIbgcdOcHa7BEQ9At3cIjvjiQmiaiw7eTnzNHzzGK+BgAz3Q0VrGYth9kMB/4rnC5Dte55Mh/+pVtkUUvEkQz8IeCYU19H6no/w+689GhIn5nf/4KJsD4Wv68N6o9zZMPwrCH170eaNNx6CO3Q8Egs8f1wb4DYEPrNQj3viAD3aunKmAcY3+ch3MruuKl8B6sa9QavGRTId9ZTpaEETngFvshYQ8LnIBBCyneiJvg+egu6teCDsHfe1HLiSmo0/DP9FWDucNVxDEAaNz4ivyBfqzlg07ngcymGlbweMN/le3F+OP99DHWIZDE5QTfyNfux9QNsj3aLmJWBg9PQCnsN68zoFM5zdCyD6oXuZvICSjamW/1eHmlKqMILSRHcBx+CypfQwpnMAAL7rTSA9nt8qJrndXWlI0xvnScUdMuAr/i2zAWHBcLrq8bi+/5697TPF6w3mJmDySdGM8PZErV69Wr6ZeGjJ0iJPW6UTa/ZJLgGLcvEVDBg/WwP4Do75Nmzo7VmVH9BmhaiKGkJKJ2c3Fd+g3eg/GE7N2KcQJ4cVgnbChvdEQxF4SFhh3hw1fdon48qUr3LpE1arDSkZfqWj1mjVatnSZw2WUxwd8Vj5v8fKeC9yTXuzOstAI+LfXXnvNZfgUzlDElqMFQNL6DRv1xptvemjGiOHD1bdPs5Wc+QjZyAmMVEV/LxQLOd+wUSJhbMa35gxS3gI37ADAV/ipYDmT/7EiCKkG9w/BLxbC4arz+YIhA+k5bmxscjscuUcMx46OvJYufUsbNmxUa2s/D8rmeTbkDr7qSYR+j3tljwWBFEhCC+HKlauMcTt48GA1NfVSNsOM5pKfB6axd3MvDRs6NNRudDdoIz7Aq7FmjYSbWSMS6v6d64noCT3s+UbPQSfiXsgkXjNfWfAHWRMbaFz3tm2b3f62det2A3SAtETvN+mFrVs3680333K17MiRI9Ta2jdqJenO9e+xMD3mpbAepgtDJ9o7vKabN28ShZbsH2QAUI7bt23Xa2++oa5CQcOHDlFra4vX1JXrjjRxrhANM/2CRR88XMv3SOtAc6qfSUu56j2S9RQDRLVC3vOOb1oQBNHtqFaQJZwJZb5u3XoPQshm04Y0BVOAVAbRlqVvL9WqVatdQ0KBILUkZrOItn8NJ+wxxRuuwOaNK8qm3/Y73XHnn7R582aX65922mm65NJLXKH2xz/c7uEDoIv07dtHl116hY499mjVNzRYOXozREqPyuh0OakqgxdSKZUyAXM3bHC8p7DpbNmWy6oAEQjQAZNJQpLP5yRx7g0IR1hA4xEF1JvFi17Tr399vebPX+CczoQJk3TueedpytQpevmll0UbweJFi11Fd9hHPqLLr7jM/WnBXvtrljui0N76EC0FD28vXapbp0/Xww894pagYcOG6txzztWxxxyrxa8v0i+vv16vv/GmR0FSOQpu8+T997c3bH0Y0QgtDXJUOR169ay1PSEDwU4xVkRPpxxCqJpeTTYiaQYlMm4lQcnaTOKpHRZ3UOOFQtEtTwxI2LB+nStcJ08+QFdedYWae/XWjTffrHvvvcf96L17N+vkk0/SpZde1qNbyv4cC7PGrCqh4dmz5+gnP/2Ze/Exng6YfICuuOIKTyJ76OGHdOv0W42BTLHSMdOO1Tnnnq2BAwa5P5IIWFCgkeCNImiYzYz/w1sGUIE0BV0L6Gb4jspliiIp5ASpiHMkM2kXTbHxkRv8cATlEM5FnynX8+QTTzqkOWTIMH301FN1wgknaOOGjZYBDz30kHPFB37oQKPc0W4IcpIr8XcsSDj3jj973C/R2iphJXXfvfca/3rd+nWGWvzoR0/xYIGufF7Tf3ebHnrkEdNh330n6ZSTTzbSXVNDowudGDtmWlWpOk4rU0559nYVBQyiIN4saGRg76MvIiREjCs6KypF8Py5nigairdcDelHDHJ4I+aHQqGg559/Qb///e+tB2rr6nTIwQfrtNNP1ciRo/TcnOf0mxtv1OLXXrMDcdzxJ+isM0+3gR4bGX8NqXfGev6aT73bexFo0dk2btqkO+66W2vXbdLJJ39UbyxZpttvv0NYv4sWvaaf/OQnam/r8JhARgbeeNONemXR4p3hQTYFnqiLLgpW1sUC/ZwFz+glxxI2ZcDfDFZs8GwJb9DLx/u7CqGn19CE3nAh/8Pix0qzq1DUq4sW6cEHH9aESRN12OFH6He332HIy6VLlxs4/9ZbfuvS8f79B+jGW27VPffeb2/u3ZahJz8XCzRGqz377GzddefdrmQ866wzdecdf9IjjzzizXjXXffqpt/8RlOmTtWgwUP1+9//UU/PekbtnXkRWraHE+UBEeD0+NGbXcgXXFlMztfb2yERJ2m9gdiI8AWGW0e+yzzgHkD6+YwBW/bGg/7ecCZWQitXrdKDDz2kN5e8pWOOPdZVi//zP/+tN95covmvvKobbviNQTymTTtGq1ev0g9/+AOtWLEi8tB7MsXfee/OuSVTWr16nW686Wa3YNEf27e1n373hz9qznOz9cqrr7qvkwEKhx9+mJYvW67rr/+lVq9e4xPuiEBH9SDwAMVXxaifM9+Vd8sI9LYyRbhGNEX4Ah3qUCSfKxTNB8gD8n6cy4oyipagwGMjYcaMBzVsxChdcOHFev311/SjH/5QL730smY88KBuuvm3GjxkiD500EGGl50x4wFt29YWLUC4El9N0DvR8z3vIbJpLF6Bjb377rtV19Cgiy66yGv6mxtu0IIFC3T//TN02+9+bxz/4487Xg/MeFC/+c1NxsUOoXy6Q0OECrrl83nDDpNGynd1qVQo2MiC7g77eyRkZIyDr2yFHPDbAVCx/KA+qFgyb/CZ8LlQeIdnft9992vevPk64cSTDP5z6/TbdO9992vBwoX61a9/JQZ5HHrooe58+MmPf6Cnnn7aaS3T3Zz4/um9Rz1eFh2BhodyySUXOWxb11Cn2toae6BUg27dvk0bN27QtGnTNO3YY8zYb771lj2kAybvp1Sqxv2c3AJhaRCCgGylnSiXrVGZvCtQf1GYwIsXLyI536giDVgv0E2YxUmDPJMtCEOE0tXgGVkASxo+fKT+9stf1qChQ40xnKurd7k7Ax3oISXkePiRR1pAPz17juYvfMVDmekj/ODYuQKxAYTXMXz4MF199VXGRAbphXYRWn02b92sZStXqanfIB1x5FFasXy5QDcj9MxIrgZgQIMTa68mzZQh8LgdaiaXF9oFQq4mhBWT9GSbB8oWwISxkjU5A6zQe0KGKZ0hChLgCeMrhv6gz/D+ww77iGfCNjf3cWiM3l74dT3wdp15HXnQ4TrmmGO0fNkyzZz5hBh3N27c2NDWZK6Lz9rDH1GAiYTDicdMO0bHHH2M+rb218qVq0XbGDyy5M03tGTJUh1wwGSdcMJJTkfMnz/f8sJoQK5KjapFI++FucyGW09ImcjLDd4K1hbh7QjIwrNRwFdOh5AkNQV0TTDdiKk28IZttaiwM/Kq8GquvOIqywJAWzLZWnV2dlm5Mj+cWcInnXSy+vZt0UMPPaItRlOj4G/XXHW8B3oqF3QzQZxGPO/8851eqKnJmCbec6WSgI9t7t2s8849VwdMnaI/3DZdq1etcv6etQPSkSwtkRLma2fSWRUroWAXUCRlgjxH4oeUYmgpSzD6EyhSdESqqiTKm2poAJcyGSOjEbYOeebggPF7OpvWhw/9sCZMnOjBDU8+MdNRE+aA0z/80sKFmrzPvmIUJDOE77n7Lvf5dqfzznvv/uy7/75HFS/WJwvb2r9Vp556qh559DH9+Kc/0eJX5uvDH/6wASnwLqJorxeZPBmN9SDcoLjb2tq8AbGcAUlvb+9Uvlx24jZHzq5YDN4LfZeM9ooYHwJh6Za6Cip15ZXv7FSeTZpKqr2jTaVil2rThCrKVsS1tfWunIMY+085QAMHD9Jdd9+ln/zoh2rI5bSPp1M0+RrwsDu7ulQsVQy0ASrKB8c7VyA29umhY4D06NFj9P3vf1+//e1NHmowbty4YNB0dUmpGnsi8AtYrVQtY81SvdjWFib/IMAZzQeICpCdhI+pak5lXGdoi7jsqVUUwbEFw5jHzo5OVfJ0/KaQxn6NecCd+XZHOqhgBQCFXBMM1L//QJ111ll65tnZ+u///r5mPvGEQFlrbukj8FoLVEcWi7a6yU1yVCo7J5N8oHd38kJsfPfr16qLLrxA8xYs0De+9T09cN/9GjthksaNnyBGKgL/R0EN8I82nqlEpfe7XDJCXKGQd7ELyFUMscjniyo7nhxwmNM1OYNoxLUfcXEVBnZ7sU3tbW0Cw5l3V9ivlYq2prcaiJ8wNu+jF5iD3w85+CBNmDhJf/zjn/TjH//Q+edPfPLT6tva6hxkAdhYqqVLFPWE2eBE5D44dluBSPsg1ydNmqAxY8foj3/8o/7tX7+l9RvW6zOf+azhQF2J7Bx+GDyA/MbD5eMYX9u2bvPAA9G731VQR2eX8ni59M1T7AhsaC4XjHMXY4W977ByVWGvtudVAweQkiILGmw0pyAx1Pi8ZYACXsTpp52qZStW6gc/+KFu+PX1mjr1QH340EN8g13tbY6ycH6iKfAM9QP8+AhBl90W48//uccUL0IXP5Li7s58wcgxgwcN0Tlnn6u331xiL2LhK69q06YtzrvhwTA/EWVJOIhPd3XltWTJWw5JMxYK5ZtKZt1KpHRCTTU1Si9bo65i3nmcqtGN+CgJPSYvy4hDbyxZom2b6lWsyTgf1NXZ4SZ66mMB0R46aIhGjx2r2sZGExWUG6yegw86WOeef4HuvPteLVz4yg40LcKXNqmjSUpuVQjBzqjs/M8vcI96JdK8CNJtHvFX1vHHH28B9+tf/0ZvL1uuYSPHBDzWmowrFalSBmgBerNZN2/eqldfedWREbwWBDMN8uT1UK5lQFVaWwyskgbkPMrxQiNye4XOLq1csVwdm7Yqlwq5XgynarUohDgV8saQHTXK00nYOB2dHSq1FdSvXz9dcNGF7jFeuXy5Vq5YaT6GhhgI/ol6R90mB999cOyyAihCLGsMKabE1DU06swzz3Co+PXX3zQOcrFEqiC0eSAA+QzCFr5hby1dutTYzh6O4irWhCoo3XTWLR8o7RGM6OvVK3i1nAOhGqUZwIZfs2qV29CSeOClkuUSURLCyjABNQcAuyBAoSVRjc6uvCZPOUBXXHWVpk+frtcWL3IUBAWLd03Ik3vztRNh+YD+u9B+9z+AiqQFaML4Cbr8iis0/dZbtWjRq9p//8nqyIO9HWp0WNv4gAfatrdrwfwFnjBEXQ85TPK68WQq0Clr6uscvWiqazDxwTLBoE5XJfLHa9es1baNG1UTVSVTAe3kJcZdqWCFC6jPiOEjlE4kncZsy3fY2DvhpBO0cctmzX/5ZYfFhw8fQSm7+ZNQNXKKg8uOf+j3Di1Q8Z289+MeU7zoIXwOmHHuy/P0xz/ertGjRzmHc/jR0/TIQw/pmVnPOFRTTcDsoUQcYOsakGbSAN/XaqQrilut1rjB9u1gtFaM1dxYk1WlnNLbTIewZeVCbvdrVktVD0To1dJHAwcPUZ/WJnVlQo8XAruOgeieLlZVfa7OXi+nABbs9j/dqbffflvnnHuuTjrxZN157wOaM2e29pk4wWGpELoIJfGVMtiuuR3l7jtZ5r0Xuke86mI2acsWhl/fp+eee15XXXWlzj33XD05c6YWLnxVo8eMdxiolM97SazMGF6eCA31zb2bjGqEMYZO7ewqqD3fqQRWZjKhIjSsq1M2aqCncpmvRThSMJHJpjR40ABVm5uVqYRiDL6IwRYM4YDmhI/qG+ptrUI/JpDc/NtbNH78eOd33l66TA8/+pheffVVNTQ2GvGmShUtyUeMMIS8vx9zMQhle1z8Hl6OzDK/NbBq+HWv/zcOtS5a/Lp++rP/dTj5o6ec4q6BpW8tEWFbOhwyOwAtdraOsGg12RqNGDEsgKuw2VTxJJvOQlklV7Ewkq+qXk0A8ISwdkQSVt/GOgVwWULIAByQ8y2XVJNOi8HmhBlR0AzxIAXlIq2uLt32xz9p5jOz9blPfkLnnXe+nnz8cT03Z5aOPgYo0zBFhx5vyAs+PIYgApsj6I2I8LtQfq8n9ztuMNahKNNHHnlM98+4Xyccf7yuueYaPfPM05oze7YOP/wIrxK5XDavM4AYYkQ/qhXV19dq4sTxzssigAvFktqp2aA3l/QQs5lr0t6XLD56gsH3QQNXDfvar38/NTc0KmPwMvgEDzereqJcRihLG9YYwwt+aGvr0De/8Q3v8b/98t9JF6V075136rk5c9RvwEDV1jftCJXDZzuVL2ZYkAF/Den3nOINHGnBxCI8+shDmnFf3lWic1980aPYxo0erWxNVrU1GQ9HaKzP6aUXX9ABB0wxGD2L0KtXb/9AUTyhlctXqRCFHqlSZTgC1WpUKSeodHUhdQg9Vkpl5/NqUikVCUtXAmQhVZN9e/dSLcISEe3+zMAzbMStmzfrV7+8TuvWrLHi37JxvSaNHa2hQ4dozeqVDjU98dhj2rB5E3EQjR83NgpRcI4PVO+O3RctBeu+atUq/f4Pf/AUqvETJmjRa2/osMMOE61DAwf008a1K/X4449pzZrVWrN8qVp691FjfYNh4VpzfX1KDEtwuotrAdAAEIOZrGZ7R0FK9OySDzLWCpBvEeiBN3EooGIzYwnTHtbYCwS1XQ8umdTBK68s1OOPz9Sq1YyCe82tRuD1Dho8WNlcVvPnzVNjQ6MWLlxg2vdrbbW3ZLZ3kVfY97H4jb9l97/j5/fWRwQvy0GU6fk5szX3hee1dfMmR5A2b9ps+M8Rw4ZrQP9+eiUax0jHAHUUKF0M8KaaJuOls0blSlHr1m9Q58YwoQpBnYzmI0M7A5rAE15o+CPQHRWJkA5h7IppNnjwIMMSvtvar1y5QnfecbtqVNY+++6jN5e86UhN//59NXbMKD30oPTYY4+qf2tftW/fpl5NDTvRsPzdsRzoaRR/t9WELgnX8jz44IMuRNy6ZYvefuttd640NDWptV8/jw+9+567tXjxIq1Zs1ZTp0xx9TK1IH37te44MUqxsn6DCm1tVr6JZDoygoOxHRvDGPHQn0eowDXEqQx0S1OvXhrYt2XHebv/Aq+8+NI8F1K19O2nzVu2OBXS3Nyi5t69NWrEcL391lu64447POyDYi/GiwajL9QWdT/fX/p9zyneCGGmJpvShHHjdNkll+iGX/9KN994g/MzhPCOOuoIx94vvvhC3fmn23XXHX8SudbTTj3V2KjcBNapfWeAE4x2kvJ8RdqJMjVZVbFQ3JMXWTguxAmbDdMJK4oCCqzZSpq4Puqa9oaySuBjhG5qN9uzVQBHP/aYozX/5bma9dSTmv3M05o4bozOPvMMHbD/fkbB+shHDtcjDz9oRX70kUfqmKOP+qCV5F05Kwgd4BWPPnqalix508r18Sce04AB/XXcMcdo6gH7qVwpaOEr8/XQffc6XzLxgCmeBMXn8Co8Qxe6RrRl01SyOVumpByUyTrkXPTWwPMghRcKq1KupUjbKEsnQoEG4WS8YTYXB49Yud6eCWnC+PG68Lzz9fPrfqlbb7rRxuNZZ5ymgw76kMhVMqHm7rvu0t13/MkbHo8IDG/4kDNyPrzu7vI3cv6jJ991sfbKJ+2FVhMaP26crv3sZ/SjH/1Iv7ruFw7THjBlqg798CE2bs85+yzddNNNuv0Ptwmc3rPOPkeDBg2wsCTsHNOqEqEO0VeZrKRdJIMfTLGU5UCk75AVeEu0j/Aa7SeOUFRKqpSDXCDMjBFm2ke8gHBGVpxx6ila8vpiPfzgDD3+6MOuxL38iit10NQpGjF0qI2I2bOf9ef323eSDj/icBeNxvTfK4n5f7ip2OyANgcffLDOP+98zbj/Pn3jG/9ph+qC8y/QQQd+SGNGjdHzc+Zo5iOPaNYTT2iffffVBRdeqH6t/fytji44d4vxhZOVFsPrjS9Gjpf6Hhu8FhKRrAjbje9GZihLIV3asoGh9fAmKFhEyXY/iIB84fOf0w9++FP96pc/974++sgjPLxjv/321wXnnavv//d/6Y4/3W5n6+qPfUyHHPJh82DIrkT6aPcT/5m/95zitYVBn5Q8W/eqq67S6aef5kIpKtoI/zQ3Nzss88UvfEGXX3aZF4TqUV6rr6/zxokdyASVNFbBoU2IuD6bhJi/sXjjAJ6b4ne2EhGLx+T2pkTR8roVdSAQ5/AEq1l7zAMAACAASURBVDhEkUlr6tQp+p/v/8B9mljIDQ31amlpscVLWGSfffZ1rg+mYnIF3lMQ3H9mVXvo03HID+9lypQD9LWvfS2sKeGjunr1ae4jKsGPOvwwTZowUczjhDY8BygJRRAwiGkU0dd5flejIowDQ8ADFnjO61HUGkBRaEGjSy+TyqqSBSAjaS85kQ59niE6EURD4C67z7Zozz337Mgw7DJ8ZK9evdSrd2974F+89lpddfkVHurBhm5p6Rs8svh6wsl2XN8u5I/es8tzPeAP8uikGKgWLxQK3i94HKxdJpPSJZdcrJNOOkmdnZ2uHg2Rrih8bFnCIhHFIBoJ8AU0rApagoRE+Je9Sv8me5H3+oG9TxjYoWw3bTsigjKGr2KxEZPARlMiof333U/f+fZ3tGnjJhuDNbmcjXLuo6WlVf/1X//l+eIQuaG+wbxBcU7gpvBvfM4e/dhtKcaMGaUvfvHzuuqqy53rZYZ2nz4tjnqw7tf94ufasm2r00T1dXXeh+gBiqzY6xivyARvISKbUWg6yv+ZD+xrIuN5U4RQB5GRK+xVj4UlNEYJkHkj2qy7EYnBGieecIJ1wfbt2/156Ny7OegmBrocctBB5uV0JuX7qK9vMA9SWxKjdO122j/75x5TvDB12AAhB4IgZSRU94MQJLzf2rePf7q/5mpRdpnbRoJFwntZPKPHpIKVy0aDKGw65wTQ9BEsHB4vZeSpTMatK2k2Ktdlyyjkg+ELxHMciuJcKArygvzEB+TB8mbEYVPjriFKN2p7xFiEkBJ/qIc/WjFGa0ALWV3tAA0auHNNeYnB9HW5Wg0fyqDzMOyc5/FYWe9gl0YWlx/CJiK8GDZZVZlkWg2ppBqYXAIlibbg6WBMGcuZWoNUKLxBcJtnwuSjmEdjUsXXzPB0frofsefV2tIifrofFAbCiPCXBXr3F3vw78FTJbogIczGjhm9y2rEYo8hKfx0P7zewPp5v/JKWFsMLeQAn/W40MiQdhiZZ+MBGPwaFdkhpP17Nekq2IzTTN2/befvVr7JhPr3a/VP/AqihalFzN8dMnhQ/LQf+Uwo2nOAZJfXevQfEYHJfCKLab9q3S28i+hECRLh4Cc+XMQW5XGtSH0uiiaJYqaVJgcMV+BDRblZpxqs7EOuFQ3M60Q2qsmqUh6SHfiC54IW91nir40eaYGrEQh73Q/C1hgCGGC9mnZtH3VBlevmLQq6f+wv/r7HFG/4JkJ43h22Gtl93hwMQoh6KMHghJltgqBf0ZtGm0HABqB6Nm38A8AF/bRURhWTaaW6ukLZOWFlhiZQyeiThE1C60C5M69CvkZdkXWcTZZUzXlXRl+ICN8pMCkPjw21WIj6ull08ogRM2A1B8ESCBus7PiTf3Gte8AbYGhoR8l9LGKDAcNGi/aH174i1jyq8XdeMGEvxiPewu5w9ARjDUg52rkYG4ZyLWxvU/uK1UqRiqBymYpH5raWS9qakvI1WffxFipSqVJyqqIi+oO5gp3XZR6Mrpdr5ruwmlHUsCbnRbjSgB+qmIPxZzD36PWYqJzZP2EJ4qd77qNRxbj9ZJAFFpih4tl8EP3N3vee24U20WpG6QGqoKk4pp8fPGZM6EQqrcb6OgtYvoWPO0hG9XGxZA+LamaRgiiVbJwxXvLdj2BAu2qZc0WK36ku48kHOEEAPDDiMQLi7/Rlv/tJe/Sz3ttOHYa0QSw3vUui/Y6niKK0qIA1IivY648OgA5AQZbL3v/tnZ3evcjkZKXk0HOVHn8+x54lslUGq7kSWgA7u9zHi77hnHW14AHs2PXd6BM4ks+hCzh2REhsXKOjqoakJF3B14GMRhRmxxEz9Y4n3vuXPap42UQcbCQWkZuMFRhAFr42TJnIS/CCcRc7uJd3BMHIOXidZ0KYKYSUQhkV3xJydj6H93NAsfKqRGXqLLE3ZDRa0II3Jm60UDAIT5FLwkILR/Bkoj98HdwHgtgh7B1eTnSS+I09/THSadAOSzH2LqEBHqmVGZvGr7PmdNoSNqaVhPcHkHqM1JDfNQXDTiGck0mroVLVmoWLNPf+x9W4epNGNlI0l1Fbe15r853a2JzTPuecrL77T9L2pJRPZ5ya4NLgFV+T+SXQPeYzoid44yE6wvc7cRyUQhT94POunozuszu5eeoDbgh7314Cax15pjwi0GKhhuLiOR+sMz/xgffqv2GCaE396J0aSYfwPeF94T2ml08DkAICe6dhDS/xXr/sANnuBAyWfhzWhCc54suCP7l2A2sAWRvJEM7id+5+uvheeuJjRMo4uul1tyxnj2OElx0WxsmqAHBE7tX0Cu1ZVIyD0R4f4fPxX0E7QMn4vPErJkn03X4twvY3D7kjIeaz6E3xB6NHaMoPcp4j5l1+92t+jK7fjBF2PN8b80l0qvf1EGua9/Xm93pTfOF4BhxYDByxdcjvEIP37Wg69jvCP/R0YZl4KgVrZMBr6mjSylUzqqYTSoO/WpOJLKHgXWMUOeqH4KyklMxmlGIIeo4CHNp7QytAOGPIG3ilXFyz83p2n6DBVXEvEIDii90PirXIM/1fFn33c+01f0c8DY1RUDGLp8BWjo4qbgv5F6vh6ElvtIo9y5CAh5kRzAGfOcf6p0ORXU2xIm1vV+ecBapftFp1AwaqPpNVfut2FbZu1/YBdUodd5Qa6upUrpY8ExYP1hZsfA3vIigz6Yw85ii+0OgxNrgInXc/MCS6H9yrn4lvuvuLPel3JFH4f4cMYO1jeWADpxJqMHZfFssOCz9eYTWZIoYMyKguF5CraD9EsXK+cqmiSopJV8FId+gvkXCEQ7kaUV1pQV4phwEMNgRiQoVvR0jDrzyCkLT7EYyFUIC1uxzg+330dJp3X7Qd2wKnCUclfpFcoUA0cjTsHTnRyHtElpv0KDTOFbUZglqIDKdq2akjWkU9LzciAW+O9iQym/2cqqkqnUGhhyjGrvTdlWjQvzufxlfNI3wVagYAzKrd8RLnhXe4rl3PtuMtf/aXnRLxz77l/b0QrIxQMcgFLV22TPfcM0MvzX1O/QcM1CmnfFRTD5zqRX15/nxNv/UWD1DYb7/JOvnkE8XED0N5BePTX2oackfR5vCTzueEa+L1aJ9bwHL3wfKNp5n4HUEQxNYMlY9UTIf18pKB00mbyO23365Nmza7z+yYadM0cNBAl8Q/9PDDmvnE47ZvzzjjdH3kI4eqsbEhXCOS4YPDKxCHXmD8fL7LLTg333yz2js6dMiHP6xjp03TyBEjtXH9Bj02c6YeemCGgIQ85rhjNe2oo9Snd29VgAVyhAmjCEOMtnlzgomdZoB6JaEmpdSSTKp3OqEawstZejOpfAzh67JDWLSOhRw/ni4b1pLc5wt0M98mElq7bq0ef+wxPfzwY+rV3EdnnHaqpk6dqlwuqxfnvqxHHnlYr7+22IU2F150oZHNfKER7SNOC6fvwfxAlh6hinG9ceMm3XnXXXrmmVmqrcnp2ONP1AknHmfo18WLX9c9997tXulhw4bpzDPP8tQn8mxsTgzw8BNyqRjtyGTo5a1rekKB6L0Wf+H14BtHwiFIx5089C604Zwo2Jfmzdf9983Q22+9oREjR+miiy42CP7WbW16+umn9dDDD6qzvdPQoUDeAi+60zd7lxP34KfgASqTac276847DAs6Zuw4nXnGWRo3brzxlhmU8eADD6qjo8NIcSeddKJo03O01Fse3HW33VrBBcctqgFARiDTYy0dRS5R95bt9lqZWhRggq1G4he6G/3daASQ0mOPPa4HHpihUrmqk04+WUcfdaRzu0BcXv+rG7VqBS1RjTr3vHP0oQMPNCaAncVu53k/v+4xxWsFGFmOIIf86Ec/1S233KrWvs1avWat5s1foH/5yle8cb72tf/U888/Z7Dp26bfplWrV+rTf/MpDRs6xB5kWDw2VMgPkmOrgv7HY7EYcgFRqbmD0YlumxIQ7Hxe5WJO5UwAPDDBdmzMbi0g0YZ7Ye5cfeFz1xqgu09LHz32+Eyj51xwwfkG/fjHf/pHUeVKP9ncl+bqX7/yFZ1w4vHRWLD3s8w94z2RenSh1Ny5L+nrX/+6Xn75JQ0cOFD33jdDS69epo9//ON64vHH9A//8Pfq3dKitrbtuufue1w1esbpp3lOr/vwopQESpccDz+gVFUKFeE1e05ysqJytWhUGxdVBNHsyEm5UIh6fYPXhGBlE79bhKKtvV133HGXvv3t74q2FaBK77vnLv3wxz/RsBHD9c3vfFuznn5aLc3Nevvtt/Ti3Bf061/fsKNwLFa6NnvjRYhJ3sPsMgu4hLRl6zbdcONN+sH3f+Ce181btmnGQ48qkfiW9t9/f/3sf3+mP/zhdvXp06zb/3i7XnzhRX33u9/TmDGjIyUZimSQq3jJhXJRZcrlyLlLyhKNitYWfomNNaJmFGoa1tVhzYDVnAX7N0p/vRtJ5r70sr7xrW/rhbkvatCAAbrz7nv04gsv6Ktf+w+tXL5S//7vX9WyZcsss5586mlt3LRRF198iXr32rXgJib7B48JzZs/Tz/84Y/01FNPqn///rrv/vsFpsMXv/Rl98t//Vvf1Lq1a9Svb1898sQTemPJm/rStZ93R4nDmJHMBgiFGg5+8HNKRL0SFcVlO5C/UsGw5ukQLma/lwsMRAiIaOR4wYX4cwdQxQxt+PnPf2G4YbzfZ555Rp/+9DU68qijNH36rfrl9b9SfW3O8oVJRv/xtX/X0UcdbT7kGmwD/Lkv2O35HYGA3Z7/P/2Jp8PBGC2mDe1/wGT9x398TcefcJIWLVqsp55+SoChz352lo488kj97Zf/XuMmTNBTT83SoleZTsTVhzAU58JyZaoE2L3MdsUiKYDba0SbYN3ylfRlAZTNp8uFLuXznWrv7FBHR6etKTahw0mcM8o7YeXiYTP1hHmh+VJFn77mGv3jP/6jwGWd+eSTmj9/od588011trfpM5/5jC6/4nKtX79BM596Slu2bPO9vpsg/z8t3t7woUjpABX45ptveLblpz71N/r617+hUaNGejIV3uOs2c+pq1zRZz//BV125dXM/NKixYvFHFRXMDo0GfLpFDVgyDHNqrOzoK580bB/pWRFhXRVXamqCgxRp5nXkRF4pqj2zi7PAm3r6FRbZz7KOYf8oXkrytNzyStXrdaCha9o5OhR+sq//bv7CZctX6aX5s0T07MWv/a6Dv3IR/SlL39Zhx9xhKeUENFxZXO03+CD7gIdAdEjgyHRIqxavdbY10Awfu3r39Cn/uZvlK3JaMHCBXrxxZc0a9Yzmjhxkv7+H/6fJ/4wt5lBGexT6BP/cDoEbldnXh3tbWrraFNnR4fbOvBKLDMihYrkJSxYLBRcXMX+R2bgUQFdiHSyVIloH285YCpfXjBfa9at06c/9Sl977/+2z2oc+fO1QtzX9LMp57U1q1b9KlPfkKf++znBBTivPkLLWc4h4VufLIe/hiJANMFQ4UpXmeffY5+8Ytf2ENcsGC+Xl30ip559lkrrC986Uv61ne+rWwqqaeeeMIwkSzhDjkNGmK5Yj2QR6abnu32mMulYrT4US1PJIzJ1UNvaM/gFR5pWyM9GEfldicTE4+ee/4F9erdrG9957v6+//3/7R82VLNmTPHU8oeefwJTZ0yWV/96ld1xZVXat7LLxpSND6Pa5n+Cs27xzxeSx2HCKVMba0+//nPGciCXrely5aqtr5Orf0HehNUEik19W5WS79+6tO3n1577XWj02AyxLm9IMaqHqDdoEZ7vAwvqNbVuUKacITbgsgbRxW0VqaA3zc2KNHQIM/yVcrnQMmGSHxIQLGhYRJC0+PHjdc3v/l1jR07Ri88/4K2bNqihsYmZWtrjZQCmk6flr4qQLh0WqvWrBWVlh8c774C5Ffwar7ylX/SwIGDHD1YvWqlRo8aY2W0aft2NfUf5KEZwME1NDR6AgiYyUrQthMYCXqm00m3pSSzOeWytSLVmqyrVTmTVjGdVCmdVCFZVZFaqKiVJJvLORwEDH86RXqY/PDO/F3kIMUs5h7yE046UWeceaYhIp+c+aQVAEPb2bgIZiIezS0tnrTCXTO1Cqs6QNVFvGR+2nVN4LHuCnnXV/fev1r6tuiKK68wug/92wxMYRh6rq5B29vbtbWtXaPGjtOAQYPcK4mQxmBDOBJ1iNcNQwzgBGAEa4x0D4hGwuHqkD4IoW1WEo+YvZrN1Tjqomw2yvGWDC8If+DzoIBjBREokND+++2vL33xC2IW94YN67VmzRq3JTKmcv2GTYat7TdwkFqa+yibqXF+mWv10RMJHO78Xf4Ni4EBhWH1hS9cqyFDhmrTpo16c8kS04FJYZ35TtErPWL4MM9npiaDYQjMWO5+4MVmslnLABLGhJarVENnw6QpZLqN3hhO37la4IdrlK4mlCoFYBU8WAbi8HnP6e7GA1wx7z/zjNOVTKY1Ztw4j7Sk74Je/kKhS+s2blL/1lYNGTLYkLjULpWKFAzSWx6uoft1/6Xf94jitQKLc6jJpPr17aMTjztG815ZpK/+27/qtcWv6tPXfEZHHnmEZs2aZQVICICJL36kSTohTyJauvRVLVu2wtft0U7VhIp8QSah3izm0rXK5wuiA5Cn3fjBTkolVFZZm9dt0tI33/KQhM50QklaSgpdnmaRVlnZZFJDBg3W8JGjVFPfYMuahWZowoMPPqDvffe7mrjPPrr0sss1evRoIy9hzRCmsIcT5ZjivOOuG/gvLffe/npYjVxNjSbvv58YcE+64Tvf+baHR3/0oydr6JBBYUA5NPfIthACJlTE+m5Yv8mG2ObNm5UAJIFQM+GjZMrFL32KVW1dttwWsFuJGBVWSoiuXfr2iuWi1q1apY5XX9WWREWlLMg1Fb2a7zLeMxSgX3fEyBEaNGiQDT3Gk0078igtX7Hc4c4HHnxYV151tY464gg9O/tZtTGZJJoJGgsGPCuESzjCY/zX3k7l97o/1oTBFyDCnXbyiXp7xSp977vf0/Rbb9aRR01zfhQAfGhNiBja4LVSWEVIOZ/P680lq/XWiqUqFLtsPLtuplRRspoScIGFSlUjRo9W76bGEO2KWpJcH18ua8vmLVqzcoXyHe2u/YAu8JBz/OWqgfSHDRms8aPHqK4m6zztvhMnaszYsXr88SeN2btu7Xr93T/8vQcpPPbYY+rqYr53wVOVnDYkdfheC9FjX9vp2IwfN1pjxyJDH3ckEchQPMl9Ju2rF16cGxRXKUx8crDTg3Mwatv06iuLtWHTRtcKYCzBI+YXVj2dUq6pQcOGD1dDNoCYuCWVSEk1YaW+es0abV2/UWkG27m1LThqKdKSxbJydbWuKRgyeLCLZBlbythPIpo//fnPdd31v9Ixxx6niy65yB5zJd+hQhdDH5gPH5wunEQirjY17G2/fwtsjyhePBPWg1F8mZoaz09d/Prr+tGPfqyXXp6vz3z2Wl1zzd+opU9zyItWCspkkgaupzKYdhCsVzyTXk29NHBgyfNXSVp7ADaQYZmUmrM1StRtV5aS/m5JdIhCDjBRzag2k1YjGJqNjcpmAogCuM7YOkwmSlYrqjNAPs3UVWUzGYey77v3fn3nW9/w/Nh//bd/83CHNWvW+T1sML4TK4cmbIYuOM/QQ72Zd5Mp8ICFLkPqnXOp6PHHn9A3v/kNjwf80t9+yWv69ttL2UWqlEoedEClKIU49HlTBYmx1duIUWFkX1e5ZGEHQH4um1NfrLC6Wm3EbylXlVFSWWqoPOgcSMCcmupyampsUJm6AHiAKsdSQLiiBxeMVTZafPD30reX6qc/+ZkeevBhXXXl5fr85z+v1pZmPffcbCMnEblpqKtXDVCkKIlS1J8Yn+SDRysivED2Yi6X0qo16x1ifOTRR3XZ5Vfoc9deq1HDhurll+Y6fEx6KOP+/oTSyaRymazSybTqa+vUv19/kdX1f0yE6aInl4L4tA3xZDatTlpPKgzYSBoKFuWKMQdWe6/6BtVnMjbogRYF0Q7kJPf6VpABjeYLDGiQ8FKVih59+FH99/e/7z3/P9//vs45+wwtW8GMWJC35IlYtfW1rn610o08aL4zPnYaY/EzPesROQAsI61XxVJVzz33or71re+oq1CyPjjzrDO1ectWYzcQtaToLpvOWv7zWWRsJpNVY68mJdm7qZTAcnD/bJT9r1C8V5u1vgjRZVPR58RAJrqJ8V9pbFDWfeQhz4sMr4EniFRlMqpFBqC60OXplDZv3qLpt92mm26+WdOOPEL/8i9f0b4TJ+i5F+eqWMhbXtU3NDiCyrWSNwb4B1hKmD9cy/uj9x5RvFw5X1qTq7FXsnX7dv3yF9fpmaee1NVXXqFLL71UfXo1OVYPCgzWbYVQbaXs/CkTacDpRWkzuQRgevq8cOPXrdugdiDnPBYw5/FthJN841EQj2Wn8AY1W9erUf0GDVSv/s3qYIqFEqqtqVFjbY1yzHLFKKmEykg2Dxtl8SsL9d1vf9tFQP/8z/9kPFk2GkKhvhYBTWVl2XM9mfVL9W1NNvP+VriHvIt1jDcOFuELL7yoH//4x2Kk1pe+9CUdcvAhNnIAwm9oyCm/ZYOKJXJxncp3tjuUVFdXo8amejU2jDbaEPShInrjtq3qKFeUy+TUUqwo36ePw4AMxUD2IjjZBAhg8v2kMQYNHaxcoqoiocpMRr1r61RLq5nrEIJligLlN4qr7rnnHt06fbouv/wyXXnFFWrp09sWdlNjkzdaVz4At8AHbFL4wrliG1/hfPwbqhx2Ej28svPvvfk37tUtGem02rZv1+9/N12/vfE3Ovfc8/SJT3xCwwYPUb6r6CrR3o0NHjZANMqzlplSls4ol85q6KCBGjhkoEpEMJjHu73No+LA8Ha4OJlQpq5OlWRVHpSRIHxI2ojWoqQ7DuoYIcieZcZzpWwY2+beLQ5jQ/RAeyCUQofDotde1S+v+7lWr1ih737vuzr5pJOCdKmU1YdJV8mUPehifa1KhU5luAbga/neeCYrvPDXSN+9kBmQA+yxajYjhl/ceustDjN/5pprdOppp9nIpuYGMItKuaSNG9arbdsWj4R1ei+T9hQhiuwsdxMJpyAofgJExV0rhJzTQbmGQoqQRLReqVSUzda4QKt3XaOYR2ZjqEqkq0HNnmoVK8mgPJH17R2drmi+9dbp2m/iJH3x85/XpPHjo4hMWcwYJyLTtm2b8ow7zOedgnLBZnon6Mr7JemeUbx8m6EZg0Lcvm2bnn5ylhYumKc5c8ZoxYqVBsk/5ZRT1NjQoNFjxuqJmU9p1aq1em72HF12+WViSDqHiyV2eJJV31xXvlMg4WfwNApFF09Y4mKtQmTi7FguVLxVqs4TGO2IQg0YASQl8kbsEhdXBSsHNCUKt9544w0tX/aW5zROn36b7rrrbmN2fuhDBzlkVqkkddONN7vqGQ/t4IM+pN69A9zdjmjj+13xvfx9CJ7Ozg69+upCLVjwigXxLbfcottv/5OHDhx51JGaMnmy7vzTHa4MXrd+nVYuW6HhQ4cas9lbKCpUCp5zKK7qLJSUyEkdhbInFcUmZlD4cm6PUCLhqK4iSEddyicqKvJcqaASvcCVlDdPXLgD/TlWLF+m2XNma+P6NZr74vP63ne/47wiCnjEiBGGC3x85hNav26dnn1mtvr0bfU81+4whC7CRlTYFYp6EDl5T9K8bK8IonXFypW66667tGzpMr3w4ova9J3vGOMY/PZ9Jk3y/nrk0cf1gx/+yJOhmFrV0FjnytSwhCEXV2WeKmHetg5vcGYzk+rNZEMOD8GaJNpFmyEV0ImqChRYlQpSoURbBFPrlUhllSlXlMY5pfc/qgmA37qKXZo1e7Zmz3nO4ew777jLLTDDhw/XhRdepMMPO8yRkOuuu16t/fqqWCwbWjDu6+1hJH5fEgw+eP311/X0rGe0du1aPfzIw3rxxRc0fMRwHXXkUdp30j6acf8D+tlPf6Zhw4e6Y+TwIyYqV5vz+YkqEn6GPoSRUXQUyZk3ANPJ1XjiVBxGppc7pgOV7XTAMHe3XMJpCu0MtQVa1QI2Q3ize2LMEO1tbZox434tXPCyyhMn6ZfXX6fpt93qYS+Mtz3u+ON0711361vf/rYLtwYPHabBgwc7Uve+FmS3N+05xesTh8wnwvfsc87ShEljPbu2vb1NHR2NnjxE0c3X//Pr7pml2IIQ9IUXXaTRI0c6dIAlSlUa1guPOWC+yKckpdpsVsVczsKcjRYEc8gV2dLCo83QOJ012EYtuJ1KWCjbO7G3E1VC7rBMEy4Auuqqq9Xe0e73ojiAh6urq9OZZ56pYqmsl196SQMGDvAko+OOP/aDsYC7MRJ/xtY+fD5kyHBddNGFLlKBVtu2bRNWa11trc4771z3aM5+fo7nrl5wznk67rjjHf4NqFW0koXcH/2AgCeQrMlkapRRybSF9lagqYCKhNcE7/D+dC6nTK5WtTTf29YKOOK8H4XNBuVa+YFvwAI/+KCD7HXzHGEt2KOjo12TDxirr/zzV/SnO+7QutWrdfrpZ+ikU04Rvad42YHtI1URKd1dlobnYomwywt75x/eu+WElexJJ52sseMmqlotOU/W1rbNaztq5Chd+7nPavCQIXpt8WKdecaZ4r0jRo50EWWQAdAp6bm3temsyni4jIVMJFVKVO0dJ5lcVE0qnQp0BAmpCmxgLgsouJHOmFaVLob3E+2i9yHwSYAGBboURT5y5Chdfvnl2r51u0F7kE0Ie+Y4M0+WCukZM2aYL884/QydcsrJxnGHijsDzXsnTf+qu4rkKimHAQMG6qyzztTq1attkW7btl0d7R1O9Zx08kk20sBIIJp07bXXekhB3z4thmckhGsOMCBKUrU54B7dte2oR6I24x5aw07GF+g9HbxPQFdslEWgTShfCjXR3BgFdMZ4W1om7AKnyAAAIABJREFU0FiR1ocPOdhjJiPbzF44ETnwpD/3mc+ovrbeThqDHv72b7/soSoY77GDYM86vpa/8LjnFC/fHhVL9Gvtqy984XMuSEGIkZCG2RubGkWu7Lhjp+kjhx5ib7axqckLwXUG74UbCUKR3B8CNd9VMOpJjoWlshjXlk2UIpAcC9EQMiqD1dxVVDFfUFcq5I1rsuE9Vr4ej4DxzOSaqjfWkUce7usxAHskJHlvDQo8ldaX//bzbpHK5XI7gPTxrGJF8xfWuMe8HDNeQ0ODjjrqKLGu7EM8BCbUEIZsaKhzdeHnv/g5Ty5iKD1REKtEF8AEt9GWLmn4SskzfbuMl5xQPTleD+V1Itk8g26zEnbOpSIViipD/0RJBfK7jIizJ4ZXRCFfENQxv+HVfuxjV4eQ1A5+Cm1tVNQeO+0offjgg608SIkA8sBnPdMj4hceuAe8rp58QG/WZvDAgbr22s86GlUqk+8rGkOZ/B3S74ADJnsUKF4MMiHnlE4UAo6iUl7HqIcTGVBgdjKGlgtacqpn/8MjUcFjNpVyD/b2clHbS3nLn2xJyharSmVSbjnDgDcvkPvDuCNNlUnoiMMP12EfPtQyjBw19Sau6YiqYa+4/BKdfvopTpdROBaMuIjSyL4PDq8AeVsO9joTynC02BTgZ9MdAG9Ab6YQXXLpxTrzzNP9WkNjo71HWsfwYjGgLV8DQwkeKhTyKuIGG6CF1GYEK4ryi9pDU0o7JUhtUDVfsL7wBaFzq7kACYssiNDywn6tegjCxRdfrAsvvNDfbwWNZ50IyIUtzS36j//4qrZu3Wb5RXqUI3jlQZlb2PnZv/zPnlO8keJ0qCkDgHQkkSQ1NnLTwY5g4TnwJuPDz/F85IUEBRhm6OI9cRBG5Hk7GWxuLBl7xcGD4Rz0e6GKQ0Q5zOCEAUjQx94J3+4r82UAO5kUI6n4fPdr5jsxFvhBCfTrF+ZE8rzf66v64J9dVyDQlhxoUHbh1Uim+g/WkwKIRCopqomhFSTmOXjHwSUTiIKZYJVaULolKKVUiaYRjC7GO1LcQJLXnwq+LPtSQFaGzYVFulNIvrMCAloiYPnh2J0HzFeVqttZaGnhINfougIXDPgph8DC3Ye/e+6/CMwAt5tOxi1cAW6TtcQQjw9aOPjhsHyAPLbfu9EJXrCCDTjeHrZSqai2LDV0lZVlcAGUhxdKVSULZXUyVIH0EwqcfjJOClQhAjsZ0k98pyd1V0M0BCNbu6KCRtdF9CXIBtqi4gN+5bB86Sbr4td76mO8B1gSDxKIFyJEkHcAWsTzdilWig+K1Lz/ovXkwdhUrL8SYhxfokLUI+rzjT4YpAZCgbA09KTXJbyPt6BaCF1bvkTnRrGTxuDgKegYy4DotOHBPeJh+hl1Pa2tLT4fL3Kv1g/x9e7ywff+Yw8qXjZcAChAKTr2HmEdB2EavAwux8IyslC4eBibu7G8ja4Xr5fiqlhQAx1YSqWdz2GT+jMoWXIBto6CMuY8hKlBrymBcVNJqZKNR8qxBwOZCFpwvRb6kXaPyOBKNa6f60ZowyR8H7/7Uqlkc0FFZJW99xr3mFdZG45YeZGvj9ctvBIEGO/za4DPQ/9yxdXifM7Lbk4AlSrQkhYefqCdB85QNBNtRujAJvJHOK/zeyUL+BLtRFHuh+swf3q7hKuJ/0WIwmdsPPNm9AK/E3WBF2EROAcLN9xTd25FLITX43P21MdA+7DXWVfWimIb6AXdd64n9IhWycItzFSNPSY+x6IScCyWS0auInebqWaVK0vrFi/UxhVr1JrOqFdNjff71va8NlaKqgztp+yQgappqrMnlKAVEF7yOS1xgjS2kU5vLz9gxUdyCLkQ0X4nL0dGeLcUhduTeiqh/+J9s1dRpGG/hD0TDbqxhxo0Is6T63qQr55WFO8k5K/dVNOC0HWxizp3eCLUdHBO6BN+4u8JshreK5dLSnB++JBhLHzHDqbbKafgM74VmvNjg40agMgQQO4jYtj7RO/ojKD7Ij5V8M7/4oLs8oY9qHjxQMPm4oqsy8jD+upQooEI3ATAFvHBb7yHG46PcPNs0oRq63KhajBZVV1tnUqMAvMsxmCpsKFjAc/ipXI1qmmol+rrlSDHlwjel30Ub/5qCAc6eR88F284BCdeEkhYDHgAK9aXxAiylOdHcn22cvwLSj/av/GF9/DHWEiFTRakKrKOI9Aowlm1cYqRFm0i5mTSy2nBxxqHDcVuSKYzrihMohhTtAMkPPKPpL8t5GjN+U4IhnIlx5traFCdyqLjLpMiDxg8Jt4On3Y/bFxFm47ffR/h8r3ZeK+Vu70k/grRmDglEq448Ibtuu4n72G/QwerNv4xrnoQoJCYFiwDDkTh3lhwwQgWfLRomTahr591hp5UqdbV1wunqSaRVENXRa89O1drbrhXYxJZDevb7Jzusq3b9FopryHnHKt9zzhRtX1aVaTiPVtVCjANWl0sZcOkrJCysr9sIUuY0/IJzzgywkL/QwglJummiAws3kdIGiO/uzDvYeR+x+3GNLUyNf3CWzC4oGeQ89AbWRs2GTI37MhgqPOJGAKSbU2/fq6Wwruk87vO9eayjmRa5yRD2icgGgYHCXAORkemo30NjwHE4SPa2+GP8K/51v2+RE2hdzpE1dAvVvBB1mdocbInzjWig0K6s/u53s/ve1DxRosX3RShPooh1q1bp40bN6pfv/5GASlHsf5Vq1Zp29atGjxksJqbm23tEA4I1gs3E06EwqaMm+exXHB5wube6UEH3Y6UDu+hp9O4zkAJMtPTQNvBMAhCEqVadcEWlhHfRViEfrGVK1a4Japfv75i+Dp5ifb2Ti1bttQ53yGDh1gIYIERTo1Z5v0s9t7/nkCzsLmCJ8r6Ll26zKHkAQMGqIY2gkpVHdvbtGzFMjPu4EGD1FBbb+PGKQFHGuHuMF4QT6VkARdQymjpYbNiKHEuaMymZiNbCLLZyBVBewQ+2tCKOSgF3sv/FvLRSwhanty0eZPzOL16NRkEn3uhqn79hg3avGmTWvr00YCBA8MsaBsIgQOsbN5lQ0dsvPeTPrpDlpk1Yz3oo8fT2LJlu9avX+cpXwYtAQq2UNCGDRu0fv16100MhDcy2dBnGxk6pBLoWCAXS0sQZMxgXFGp2t6u9KZtqktk1JBgsFRC27ZuU32hQ7Vb2pTtKCrdVVGJ1kHInY6FehDxDnXxqwuzYI+Ew94UVdKFUejqUv8B/dXQUG80ra1tbS4Sgp/BHgeEBU/eLSwhUegVsAHYY6j9bje6UwawPqFzIKHlK1aK4qr+/Qe4dRTvBxjY1atXmRf69QvPYyC7PRChHu0nFB/rjgxA6TrIXyrJ03Uj5W0FHUUo+agjluiLKGqKgrTxHxlO3a8cNuA7MBTp9d3W1uZKbHLRra2tVtjUKACqsmnDBhEe5z6oakfmODrra4t4q/vJ/8zve1Dx0hMFI1aFcqUqbeXq1frV9b/S2jVr9elrPq2pLX301vLleuCBBzwkgalAVKudeuppOvqoowxAHiwPPJ4QGigWCgbmYINkKb7Jd3kBUbJ4ylbU0c1x2xRWdXV2KJ/PqjMC0GBTVrGQHAoPipiPoHAxsAH+oABs3rx5ug5M0YMO0vkXnK/6unrNnjNH99x9l1asWOXIx4RxE3TJpZdo1MiR9tj+zLr20KcD40FDevUwWubNm2/g8fHjx+vSyy5V/5oBmj17tv7whz9q89bNnmIEKP2FF1+sD02ZEnkPEQMjxMuhlaAT7yJVUa6zolJXl40vCGBBF23QEF0BqaygPHi+aakAOEcipUKuzrjrtrLZ03wm2rQUYgCSAELVbdN/57aHj3/8Ewb8oDXuht/cqGeffcZeEDKWCugrr77a/ahW5ZwruoYdhN/97x0v7N2/sKdYW3K55Fo3b9miBx58UDMeeEjHTjtaV3/savfkAph//4wZLpzDwD3kkEN0zhlnaFD/fqYLStdGcgWw+6IKnXmVqtQGpFTXhWdcVCpHL21SKSZSlcvKJMtqzKU9JL0r36FSZ7sKlbQdgJpUVbUiRx8RxqcPxh39v7Sfbd9eMLzpzTfdJNpLvvilL2n8uLFui/n9736v+QvmW/CPGDFSZ55+mg466CDVMH40yvfu3ZR9/3fH7mVfwgMdHV1iss/Pf/Fzr+knP/kp7bvvvp5ed8tvb9bChQvdzQBgytFHH6kjjjzSjpj3FUEse79lO0Wd+bztZ4eaRcdLLnLCeDe0NMfY8ENvlPJdShXpeqnYO64v1ewg/+53w/UyUa2jvVNPzJypGQ/M0IFTp+q8C85XbV1VT86cqd9P/702bFxviNsDDzxQp556ikaNGm0d5PNFYmv3c7/b33tO8SKRKOdXStvaOjT9tt/ptum/1bOzZmnipH10Zf5qb8glby/VD37wffXrP0AHfugg/eY3N2jjps0aOnSoDj7oQG8MhyksGUOOFwISHGJxyAG5qIrQNRFhg1uE/BCIJOR/CW5hiZZLGDGEGGNPOiwBe47Tk1PIF6ua+9I8XX/dzz1J55WFC9Tct6+qiZQ6C0U9PWuWfvLjH+uyK64yRvNPr7teffu1uvWgObOzMODdFrfnPReEmkcCzp9n5Upv3KuvvqJPfvJvnG4ADu7ee2fo5//7U338U5/W9rbV+vUNN2rYiJGaOH6CelOJF8lG1g/DyMYckQ97FnBCFLGohJxNLOz5GNERPC5/DlhC2sky0D+Etjknxi2HWUzSpo0bdOedd+l3v/udAHFnyAbVjfDb66+/oV/d8Guj3Zxw4sl64P57jWZ13AknqHH8BKWN08oVhMuOQ83d92C32wlfvBf/ixJDCG7YtNm92zMenKGXnp+jNWs3ady4sTaW57/yin5x3fVaumK5zjjtFD0w4wEbvYcc9CH1H9hfSaei2Ov06FYtPFMF8vq0eZWVLgakqiqV0gjMSpfBeIqJktrzeaVKXepUQclKQQUXwaaVwUiLCR6oHyhGmLNc0Ytz5+rmG2/SC8/N0aJXF2rU6DH6xKc/rc3btun+Bx/S/153nSYfcIBa+w3UzbdON9jPuEmTNADw8Gj2eOCpnkTtd2dkVoC9s2DBAmMiPPboo5o9e5b22Xc/DyvAo5zxwAO68ebf6oDJkzVs2AjdfNONnv603/6TjXBooBRvIs4WZL8BVAj9UgwVVT0T4XIxlR3koHztvUZ6wpXr1gtBJ8T7Mn40zUTrYIfuvec+Tf/D7Xr5hTkCBKpP3z6uel+2dKl++r//q3lzX3b1++ZNG/Vf3/uO+vdvNexk8OojAfDuS/KOZ/eY4kUmErojYgccZHNzL/fGLQEYuw6Un4Q9ju1btthdP/roaTrx+BP08svztGTJ2+LmPjR1ikvKye1yEMrN1eTcuwcQtYdhR328oVo1KNS4CCeVyihTW6Pa+jAkge8EyYYwMvlBvGgfCRCPbCPZSmJqysjRI7W9fbveemuJhTQvANq/ZcsW1dbV6tjjjvEUo4WLFmneglcMnt/c1BC994PNFhY2sDP5HNpGBgzor0mTJmrp0rcjGqS0ddNmLVu+XM0Dhmja0dO0fOVKLX7tNacj2tva1dzUaMVocHRg/nI1zvEmgCHM1KguU1GqpiZa96i6MYp+cA3k52vqalXfUK9ioqICOV+ux3CfEZ2iBxQwV4xSBqZy33320aYN67V6zWoXWqFOAXbf0tau004+WcefcLzWrl2lZwEFWLfWQzVSisfN2QS0lxbWAvMvKORdLInw4l77r5NErh5OqlfvJuOdb924SfmuRTtqM5a9/bZWrVqpg6ZO0akfPVUrly3VwgUL7XViuhOh8nmgUzanmtpa1UWpAwqPs4WEUtmcUuVAP2iIV0PODcMnncsq21CvdFODkmAxJ9OirzOdhFqOfwkQd9PeYl1Gtxs6dIiR9BCsyAzCjoytZKIaGNGnn3666DNluhrps2Khy3SMqbzXEvX/dGNVgVJIym7EqOFavPiVsAdTKcOFArBCn+9FF19sQJ3777trRyifr4M2UUDKexGIV5woqIYyrUbohew63m3DmvRThRZS5nLXKMPep742JGPtWcf5eFjLfFOh+I+/Eh6QwtCGTevXSKQc04FnmG706vz5mjJ1sj7xyY9r4YIFeuqpJ7Rx82aHqF0db48bK44fztdNFIS/dvl3jyle1Fi8CODkXnzBucKC3bpls3M5SNNQsVi1csVKIQfQUFur5flOexkFenDzZVtFxNupikPxdcDgQPMCpLB9u4saeN0LF90huUGs7XxH3rnjjnRFnRRKJZPqyGTU1d6hmlTCkJF1NTXK0c4UVdLtP3l/HXboIXrs8Sf04vPPO0xqzzmqduUrCKMDzgGMJNaRQ5a7LOUHf8QOBcPjp0yZ7J9nn31WTz75pLFbYXW8FopY0qmM+QCFCP4xOflCV0GdnUUDmVQqzBaStnd0amvbdhUYUgAMYFdZndu3u83ALSR4tckA/Yili6WNwUSIc1uirIL7dxOq5LvU7uKK0D5UV1cf9eNKzb1769xzztbZZ52hf/j7f9Att97qqAp5ZPcfFqiKpMCKtrSUN3IX6RTyjRHZw9aNeTxWtXwqfkcP4Q9ut1pRa2sfXX7xhTrztNN03XW/1Kqf/FgJQsUsSTXMUyanm06kghGFEVQuG5Uun+9wHz6LXiyXnRvc3tlpmZajwCZfdQ62So92CuGYdm9vWmllkllVihW1b29Xaus25Wsy9sBzmbQqXZ0ePwe4RjaXVX1jLyPbISinTN7fP0uWvKW/+7sv660lb4YBDBTSAVlbrYg+YWS0QVmgfRQ6ifm+h1D4fd0mRss++0zShAnjDcELUAopPeQmhjkKENz72ppaG+lUCROBZEkZoLFp89aAv5+sqjNPGojRjgXUrtsIkxhXNVlVshTfolzD3ifSST4WGV1o61Ay6kjhoovFLo+XRFNxHfQS19TUWmaA0XDyySfp8MMPF0h7119/vWWSDUCibqWiPWsm1lGox4Ql0pxx2MyK34Y2Zthf3vN7TPHa6rDW5xZDoQtClVFM3CQl2B5UHHFpfGlUB1JtRnELMxRXLF+ulatWObQMIHqGAiesWZRqTY2SW7eqqxTm60IkCz+iycmkW062tW3Xhs2b1KEu5bGAyDUAN1guGru1Jp3S4AEDNWTYMGXqQhiaMV9UssUFNghv7gHvCebwtUabDAsASy68J4RUgu30vvhxr35TvEQUxLF2rhCNwnD8zmZjLVnTxvo6/25jzeDoGVuKIFwxy3fb9m2hihGDijYuCmtSaYEEuHl7m4dnhDx/WNKYRuSVN29rU3XDRm0XLWghLL2uuFpVepGqFQHwwaiyQYMokgpVzHg4xSLph7AlXLQF6lGaPu/QhEgYmzRHEBp8Dq6BU9ycZp7tcYp2N452YZX7IkMvJS1arKHbvqIKUAQWMiFUswaByXPsP9rGVq9crtWr1nh6DTld3ggPQO8sgCyFhLYxQjIupgGnHe8mnVa10Gls3y3btkmba9WZpsArDMhYVSgYPpTO8X6DBmj0mHGqydRY+YPnjWgKkZHwGXgT2vIc10suFz6jT91GWCTLYr7fbSl65J+xXHTtzY6hBwEjPaY78pL3sfegIfKCv628EsD4djjFs3UbMsAWb+g0ifK95P+zTQ2qb2yS6qNiPotsivGoCSFfv13tm7ehba0gOf+6tWt5s3H3qZRnRvigQYOj62DoUQDbQXYFRR6uy9eGnEAWuYsGlyCEu4ME4DZCEZ9TLRZG703+Pad4vZmCEINBA2hFQBQKRAiCl/AxF89GBAEI3kUQw8goaXK9La39ooR1Qts2b1MHijYh1WWzKrUx1QZrIxgbCEF3IFTLyqRr1NjQ5MrThr5N6vKqJDxVorEupxytBRXA9vFc066S5jrjkAaVsMGACNftTRhtXKrtshgSbk1JWgCztNHee+9V7iGvQleOWJnxu8M8XicELcIxo3QmbVByqhfxdkNzu4wuhBXKXORylXx9Qp2lLudbmIWMh9RUkIq9mrQBojEqDnCFqDXMQjKTVe9eTQI9jSEJBSZSJZLqVVev+lzOYAsQjUk18SZio3HAt+79I/8fGYtMMSFqAp+FSUqh6I/n3rm/3vmMT9yT/mEJoha/WFkhxAgeB2VFOiCIK7wT1pS9hZJDVQNSQNUwsHzQk8+2dXaqrTMPuKNqEgn16gKAp16dDCdyGNFfafpBS6ZI9enTrHS/VnVm0q4RqIUv6uuYLiolykoRekZRh8s1hfidFiGMK+9r7kNAiob3cm5+j14M7W8fyIBduJu9yAFdvC/jdp7oXSgv5AA8gDOG7q3NBXlu+QGaYG1OY8aOskJmrTs788Z/L7lHP/Ty0jbKBCLLf8BSUKjs42jYBmh4OaIh5j0UZVK1tTk11NdFaYxQxc7lwqfIGsQXMsATh3jOvBF4oVLGeWSuNxPqQp83ITnuM3bO/prdv+cUb2TFdKcCC0nYD5xTyvQ5GPvHghF6mDnzCReqTNpnX2823P1Ufb16RSexHKfpvqvLCfWGmhoV6rY4b+tWEMf2SagT9gl5oSz5vaZeyjY2MFfBRG5gTFx9vWpRvJwUZqBNIRUa+625EQbVisMhxa4uV0kiBGACQqPPzJql9es3Kt/eprGjR6mpodFXGema6Ip79kO86bqvAozZ2UkqIW9vhlzqsCGDtH3TOs2ZPduezfK33lLvpgY1Ntaprp78bK1lG4zf1pW359tRLCqXqlFjV8WjxMjjwF9gOxvNqJshVltbp4YmIN3KylPul0ypb3MfT6iKr43PBhSlYMXGdKQaG37lNe5n4ICBnm40f9589W3pq9cXv2Z4w5YWBqLvwe0TX9j/zx+9CxOhwJFbIWXDiDhCf/AANB3Qf4D69e+vhQtf0aOPPuK6CqJeGFFhLGTzjnAdyjm9ZZuSqTYX12XJxYHbXZNV3i4zZ0T7RQ/UdOSybvnLNjQqnU1bQWJ0tfRqcrrJnoukQjW0myAT7M3S51suqdMTs7qCws7VGpebiVsPPPCghgwZYm+KqEloJwzf+8G/774C7DPWFtrzUyqEsaFMfNqyZbPuvvsuvbZ4kdv1Jg8cbIWczabVv2/LjhO257ucOuosQJMA+ZoAixlFC0ALyISppAoU3Lo1NOsRjoShMxVEeZGQqGEhW3o3OboJ1wSvlq/ZiRvAX/SaIwOYQsT1k18ePWa0Xn/jDf32llu0bs0ayweqqoPXHiKvIdW647Lf85c9Kjl2CF4XlwWvdtzYMaInsrYu4LENHTZUV139Mc2c+aQefPAhtbb21+mnnqYJ48f5JiASh5uly1UVCqUweDhN/J8wX2RiRpZV+BMLGs+X4epMJKGdCVQkhGrFISswn4su3AgIclwrFraxW+0yM+a1TuPGTwhTJ2hbqK3V1ClTdfS04/Tccy/4nGAQUxjGxvvg+PMrAMNyYEwxeYr+TQRVU69eOmbaNBdUzZo1y/Q97PDDNWXqVDXWN3gjYVQR4aB6EaMnTBopq5woB7hGvBy2D+GdyOALNQZR0B+rlekk+EiR5xrOEaxwrgv2CaFiLNnwN5uICsuJEyd5s/G+iRPHu3Vk5syZevSRR2z1nn3OORo6ZLCtbe7St7rjlzj4FNu/8aOXY+//xxuSnRVogc/Y2tpXUw+crP4D+lk/Tpw0UeecfZYryR966GHV5Op14kkna+Cg/m4XcvrIBSoYR9C8ZE8UetIalsCLQQAzBzcZIg/xKhsJCSAOT6cpO/dbAgXPaHZljw9NprDmMbRDKNlyiz5PkLGyNRo+fKSFOSmlPs29PSCdAkAMhRUrVriN6IgjjjDO+95P0L/uDuN9HyskHolqjBw50v26Md79sccep9dee10vvfSyFsyfr4MPOsTFa7169bay41u9pRyKBomu6PZEy3n2L/lg3mRvlShKQplEypEynCoiF7QdwiLWG7S68lwEKxzuijOw/8205k2UeEtLi/bdbx9PUuJ9Q4YM1qWXXqIbb7pZTzz6uD3nq676mPkAb5mDc/Df+z32oOINN+BbiPorW/v21Re/8AXlC122crlNBPA111zjKS9Mf6GwBXANqqBjorHnuAmHn8j9kIwn5BfliCAm1jECD6uFXk82FusHUgljAAHBJrfkpXArSSjmssfLB1kwPGIUcNREP2HiRN14402yxxRZtNOmHeUCgTVr1nrBwWzmB4CQsODvd6l7zvviTQc96d/97W9/awVsoJRkQod+5FBXka9eu850HNCvv0PDtly9EUJhoPkBo4h0RBp6EpYsKhMJW74Hhud9hvU03JuUongHHgAzmnxcnIs1vUOLEtTg+8wKQQbb27rqqqt0/vnnh17Cqpy2+NxnP6Nzzj1bHW3tAexh4ED1RkB42/ryum05i4PolZ5D8+53Ggsg6IIxe/JHT3HRSmNjo9esb9++ApCe8XBbt251NSn5dl5H3KIAUyApu4ASI4s9mlKaPC55w0IpTJ4hDRTRn9xafPCrdav3NgVXaQ8+h94hhRAqmuELQFgSVb6LgFdC/fv30z//0z/5776tfX
D. Thermometer Z
Students at your school have been burning their hands on the monkey bars.
Which would be the best investigation for determining the material that should be used to make the monkey bars safe for students’ hands?
A. Measure the temperature of the material that the monkey bars are made of while the bars are in the shade and then in the sun. Compare the temperatures to see which is the lowest.
B. Measure the temperature of the material on the ground under the monkey bars and compare it to the temperature of the monkey bars during the hottest part of the day.
C. Measure the temperature of different materials on other playground equipment after the materials have been in the sun for several minutes. Compare to see which has the lowest temperature.
D. Measure the temperature of different materials on other playground equipment when they are in the sun and in the shade. Compare to see which has the lowest temperature.
C. Measure the temperature of different materials on other playground equipment after the materials have been in the sun for several minutes. Compare to see which has the lowest temperature.
Tomas found a hard object in his backyard. He told his friends that the object is made of many minerals and was formed over many years. Based on this information, which object did he most likely find?
A. A rock
B. A fossil
C. A bone
D. A mineral
A. A rock
Austin found a mineral. He wants to classify the mineral, so he wants to know hardness level. He knows that his mineral scratches calcite and can be scratched by apatite. What is the hardness level of the mineral?
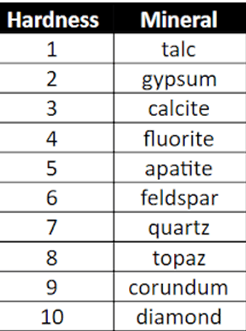
Fluorite
Answering which question would help a student decide that sunlight is a source of heat energy?
A. Why do car tires feel warm after driving?
B. Why does water boil in a pot on a hot stove?
C. Why do ice cubes melt in a glass of water outside?
D. Why can rubbing two sticks together to create a fire?
C. Why do ice cubes melt in a glass of water outside?
Sally reads the temperature as 65°F at dawn. The day is sunny and bright. She checks the temperature
again at noon. Which of these is the most likely temperature at noon?
A. 0°F
B. 30°F
C. 65°F
D. 80°F
D. 80°F
A solar cooker is a device that can be used to cook food outside using heat from the sun when electricity is not available. Ernest is going camping and wants to build a solar cooker to cook his hot dogs. Below is a table showing the choices of materials he can choose for his solar cooker.

What can Ernest conclude about his choices and which option should he use to cook his food the fastest?
A. Choice #1 is the best insulator so he should use that.
B. Choice #1 is the best conductor so he should use that.
C. Choice #2 is the best insulator so he should use that.
D. Choice #2 is the best conductor so he should use that.
D. Choice #2 is the best conductor so he should use that.
Kevin was given the following clue card to help identify 2 samples as rocks or minerals.

What questions can Kevin ask to help determine which sample is a rock?
A. Does the sample have smooth, flat sides? Is the sample made up of only one material?
B. Is the sample hard to break? Does the sample have a rough surface?
C. Is the sample made of more than one type of material? Is the sample dirty?
D. Does the sample have a rough surface? Is the sample made of more than one type of material?
D. Does the sample have a rough surface? Is the sample made of more than one type of material?
Use the Moh's Scale provided to answer the question

A mineral can scratch talc and gypsum, but not apatite. The mineral is MOST LIKELY _________________.
A.topaz
B. quartz
C. fluorite
D. diamond
Fluorite