Characteristics
Graphing Quadratics
Maximums/Minimums
Intercepts
Application Questions
100
What are the positive and negative intervals of the function below?
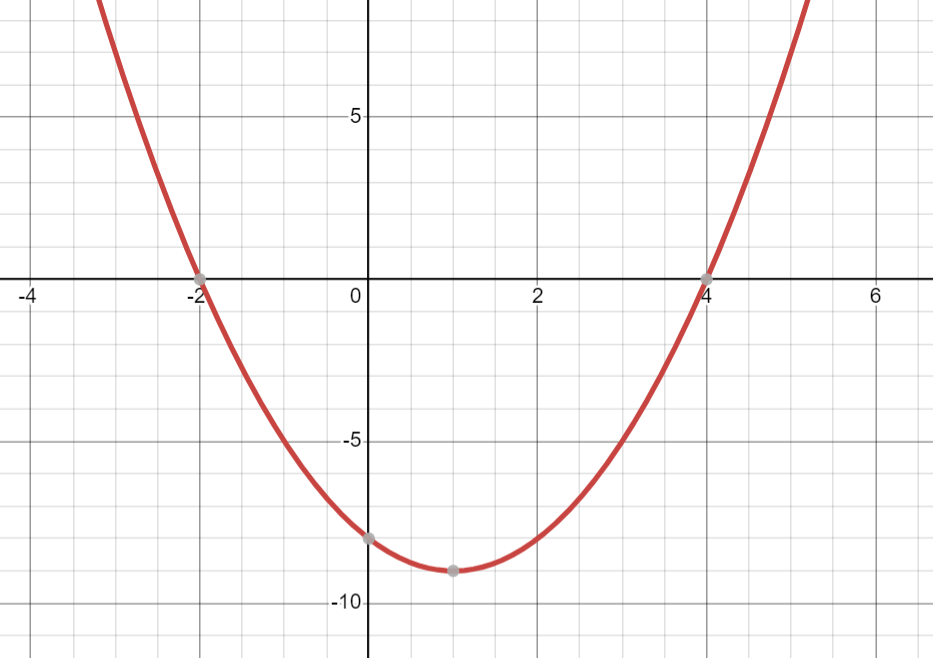
Positive: x<-2, x>4
Negative: -2<x<4
100
What is the vertex of the parabola?
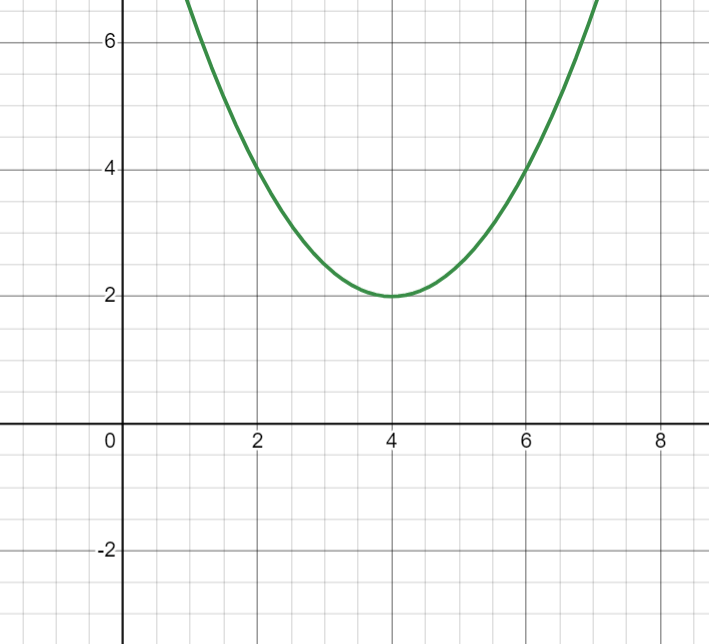
(4,2)
100
Which direction does the graph of the function below open?
f(x)=-3x^2+4
Down
100
What is the y-intercept of the function below?
g(x)=-16x^2-72x+102
(0,102)
100
The graph below shows the path of a golf ball after it was hit. Find the height (in feet) that the golf ball reached and how far it traveled in total (in feet).
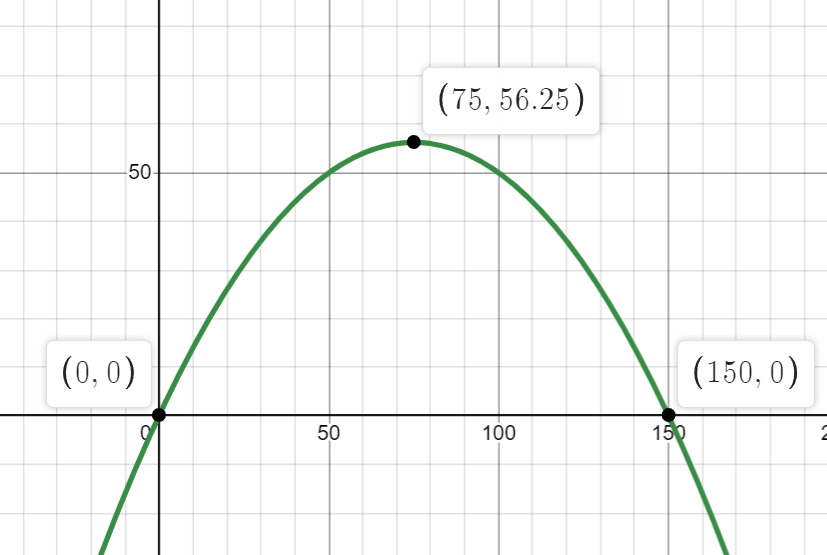
Height: 56.25 feet
Total travel distance: 150 feet
200
When is the graph decreasing?
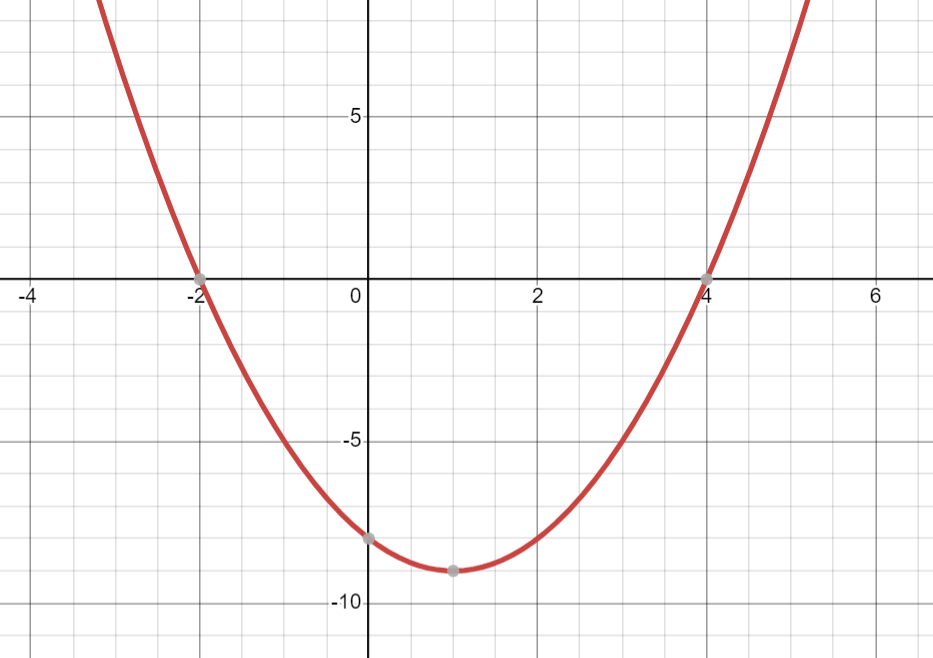
x<1
200
What is the axis of symmetry of the function
f(x)=-4x^2-16x+8?
x=-2
200
Does the function below have a maximum or a minimum?
g(x)=17x^2-6x+1
Minimum
200
What are the x-intercepts of the function below?
h(x)=6x^2-54
(3,0) and (-3,0)
200
Find the maximum value of the parabola that has an equation of
y=-2x^2+12x-16
Vertex is (3, 2) so the maximum value of the function is 2.
300
When is the graph increasing?
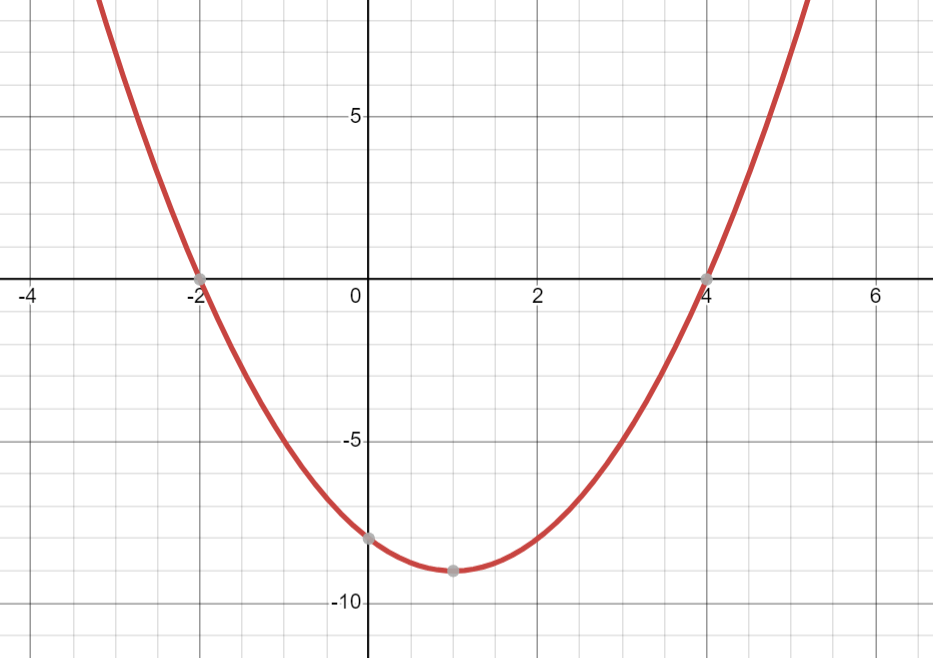
x>1
300
Graph the quadratic given by the function below.
f(x)=2x^2-12x+15
300
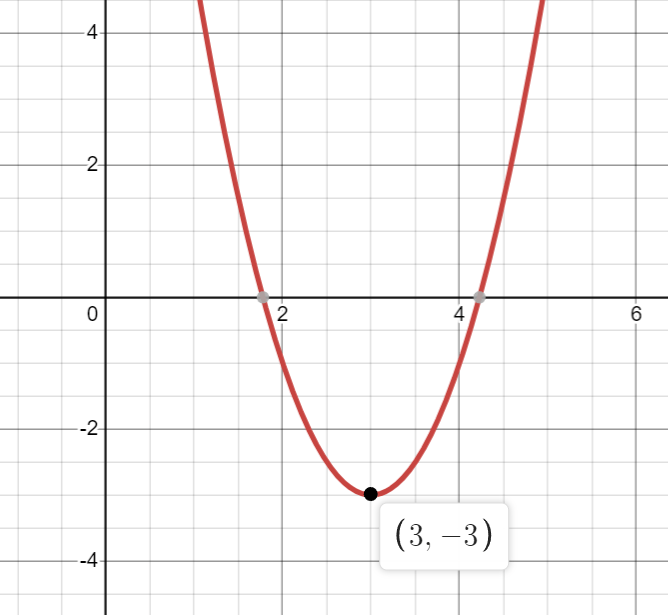
What is the maximum point of the function below?
f(x)=-3x^2-24x-47
(-4,1)
300
What are the x-intercepts of the function below? (Calculator)
f(x)=0.5x^2-2x+1
(0.586, 0) and (3.414,0)
300
The altitude of a person running down the Sleeping Bear Sand Dunes can be given by the function below. How long, in seconds, will it take for the person to run all the way back down? (Calculator)
f(x)=-6x^2+1560
About 16.125 seconds.
400
What are the domain and range of the function
f(x)=2x^2-4x-11?
Domain: All real numbers
Range:
y geq -13
400
Find the vertex of the parabola given by the function below.
-3x^2-12x-7
(-2,5)
400
What is the minimum point of the function below?
f(x)=2x^2-4x
(1,-2)
400
What are the x and y intercepts of the function below? (Calculator)
g(x)=-4x^2+7x+2
x-intercepts: (-0.25,0) and (2,0)
y-intercepts: (0,2)
400
Suppose the height of water falling down a waterfall can be modeled by the function below, where x is the number of seconds. If the water starts at a height of 1250 feet, how long will it take for the water to fall into the lake below? (Calculator, round to the nearest thousandth.)
f(x)=-16x^2+h_0
The water will fall into the lake below after 8.839 seconds.
500
What are the x and y intercepts of the graph below?
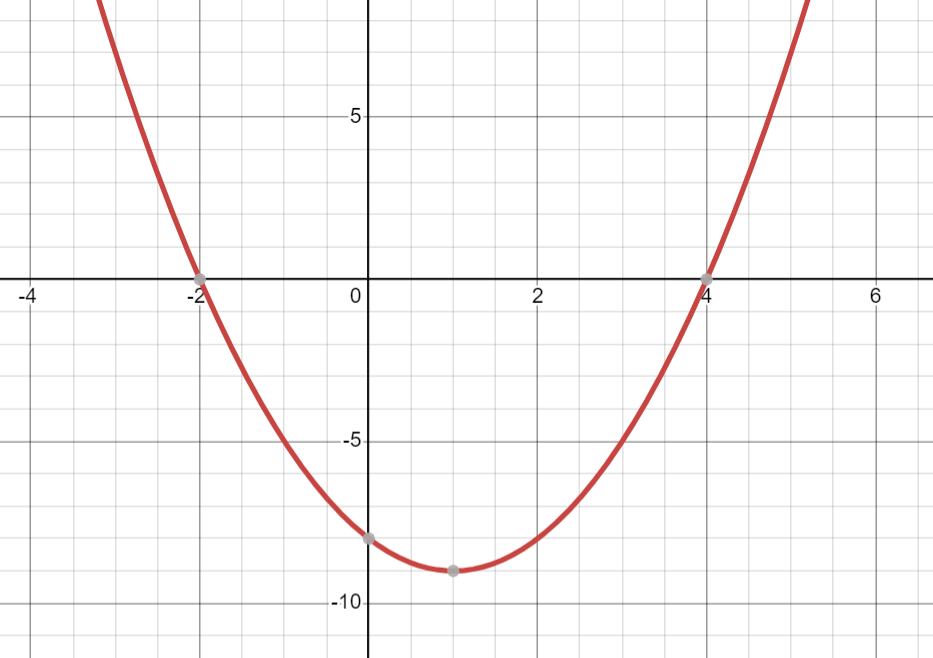
x-intercepts: (-2,0) and (4,0)
y-intercept: (0,-8)
500
What is the axis of symmetry in the graph below?
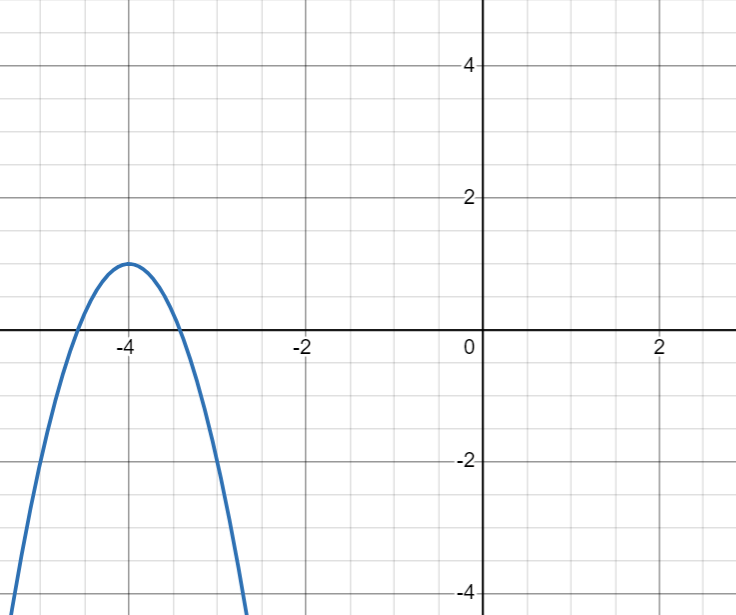
x=-4
500
What is the maximum value of the function below?
-x^2+12x-33
3
500
Find the x=-intercepts of the function below.
g(x)=-7x^2+28
(2,0) and (-2,0)
500
Write the equation of a parabola that passes through the point (-1,8) and has x-intercepts (1,0) and (-3,0) (CHALLENGE QUESTION)
f(x)=-2(x-1)(x+3)