Least-Squares Regression Lines
Interpreting
Residuals
100
When x increases by 1, we expect y to increase by m.
The slope
100
What is the direction of this linear regression?
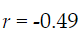
Negative
100
How do you calculate a residual?
Actual-Predicted
200
When x=0, we expect the y-value to be a.
Y-intercept
200
What is the strength of this linear regression?
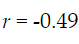
Moderate
200
Use the point (7,4) to find the residual for the linear regression.
-1.5918
300
DOFS is an acronym to help us remember these four things about a scatterplot.
Direction
Outliers
Form
Strength
300
Interpret the y-intercept of the least-squares regression line.
When x is 0, we expect y to be 6.57110
300
Use the residual plot to determine if the linear regression model is a good fit for the data.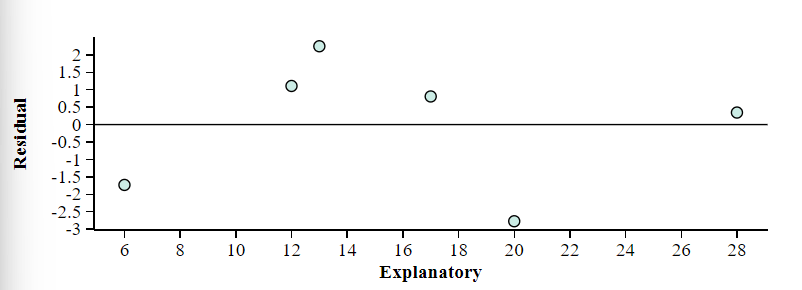
Yes.
400
S represents this measurement about a least-squares regression line.
Standard Deviation of the Residuals
400
Interpret the slope of this linear regression.
When x increases by 1, we expect y to decrease by 0.1399.
400
Does the residual plot indicate this is a good model for the data?
No
500
___ % of the variation in y can be explained by the x-variable.
r^2
500
Interpret r^2 for this linear regression.
24% of the variability in y can be explained by the x-variable.
500
Which residual plot does NOT represent a good model?
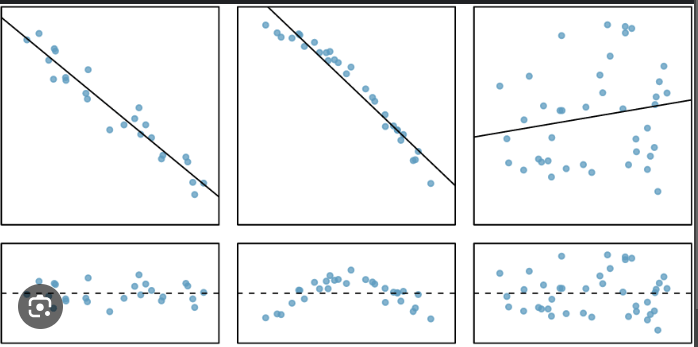
The middle plot