Transformations
Domain & Range
Square root of a f(x)
Solving Radical Equations
100
This type of transformation occurs when you shift the graph up or down by adding or subtracting a value from the function.
What is a vertical translation? What is k?
100
The range consists of values that are greater than or equal to this number?
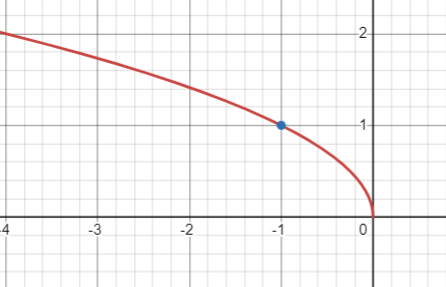
f(x)=sqrtx
What is zero?
100
Use the graph of f(x) to graph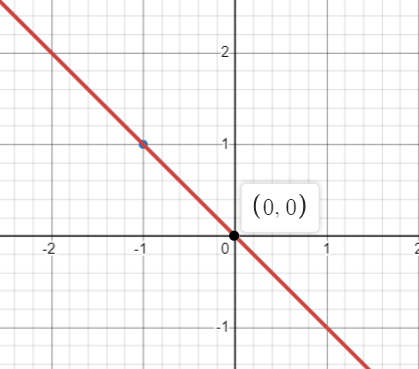 
sqrt(f(x)
100
To solve the radical equation, the first step is to apply this operation.
sqrt{x + 2} = 4
What is squaring both sides?
200
The graph of the function, this transformation occurs.
y=-sqrt(x)
What is a reflection over the x-axis?
200
The domain of
f(x)=sqrt(x-3)
What is x>3
200
The invariant point of f(x) and sqrt(f(x) can always be found at this location
y=0 y=1
200
When solving radical equations, you must always check your solutions for this type of result.
What are extraneous solutions?
300
The equation for a vertical stretch by a factor of 3, a reflection on the y-axis and a vertical translation of 5 units down.
What is
y=3sqrt-x -5
300
For the radical function, the domain is restricted by this condition.
f(x)=sqrt(4-x)
What is
x\leq 4
300
The trick to finding the y coordinates of y=sqrt(f(x)) when you have y=f(x)
Is to take the square root of the y coordinates of y=f(x)
300
The solution to
sqrt{2x + 5} = 3
What is x=2
400
The function below has this transformation.
y=1/3 sqrt(5x)
What is a vertical compression of 1/3 and a horizontal compression of 1/5?
400
The range of the radical function starts at this value.
f(x)=sqrt(2x+6)
What is 0?
400
The domain of y=sqrt(f(x)) consist of all values in the ____ of y=f(x) for which f(x)>/=0
What is domain?
400
The roots of the radical equation.
9=sqrt(2x^2+9
What is x=-6,6?
500
The transformation for the following radical function
y=7sqrt(2x+20)
Vertical stretch of 7 units
Horizontal compression by 1/2
And left 10 units
500
If the square root function has a vertical shift of +5 with a vertical stretch of -1, the range would be the following.
y \leq 5
500
graph the function and the square root of the function
y=2x+3
500
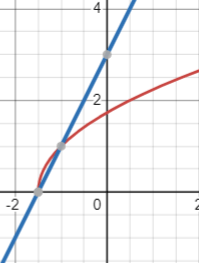
The solution of radical equation.
x+3=sqrt(18-2x^3
x=-3,1