Rational Functions
Applying Exponential Equations (Part 2)
Equations of Functions
Applying Exponential Equations (Part 1)
Solving Rational Equations
100
Identify the vertical asymptote(s) of the function:
r(x)=(x+17)/(x^2+8x-20)
r(x)=(x+17)/[(x+10)(x-2)]
x=2, -10
100
A population of microorganisms is growing exponentially by a factor of 2 every hour. By what factor does the population change each half-hour?
2^(1/2)=sqrt2
100
Determine the equation of a rational function who has the following characteristics:
x-intercept: (2,0)
y-intercept: (0,6)
vertical asymptote: x=1
r(x)=[3(x-2)]/(x-1)
100
The population in the town of Huntersville is presently 38,300. The town grows at an annual rate of 1.2%. Find the number population of the town after 9 years.
P=38,300*1.012^9
Approximately 42,640 people
100
Evaluate
lim_(x->2^-)f(x)=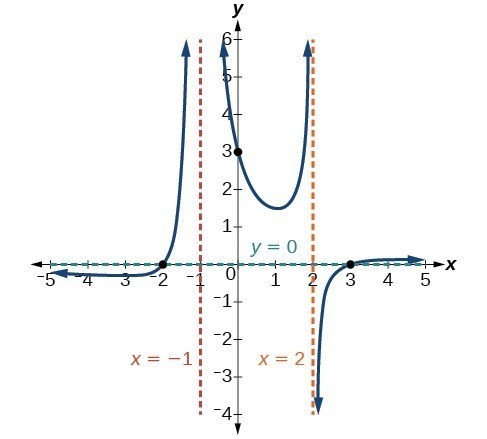
lim_(x->2^-)f(x)=+oo
200
Identify the vertical asymptote(s) of the function:
r(x)=(x^2+2x-8)/(x^2+15x+44)
r(x)=[(x+4)(x-2)]/[(x+4)(x+11)]
HOLE @ x=-4
V.A. x=-11
200
A sample of Iodine-123 weighs 3.5 mg and has a half-life of approximately 13 hours. How much of the sample remains after 1 hour?
3.5*(1/2)^(1/13)=3.18 mg
200
Determine the equation of the functions graphed below:
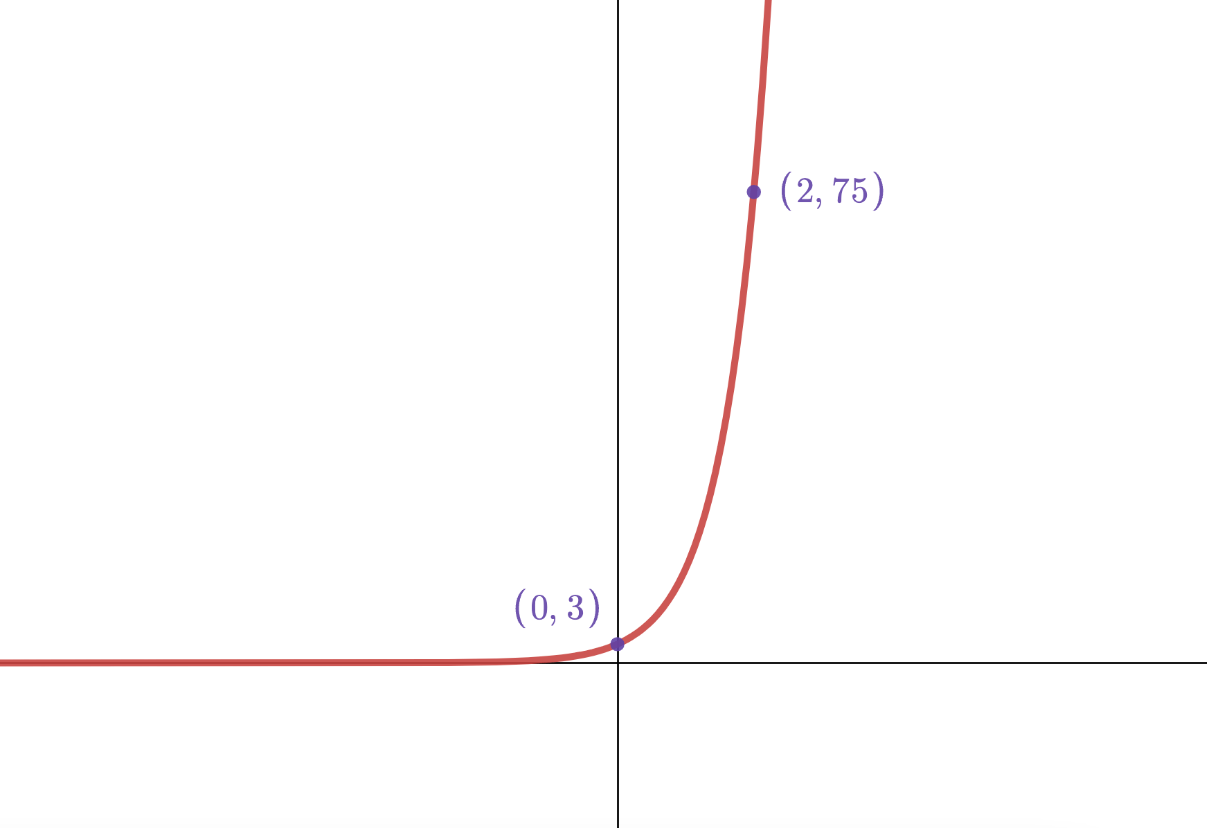
y=3*5^x
200
$1,200 is invested at an annual rate of 3.2%. How much money will the account have after 12 years?
A=1,200*1.032^12
$1751.21
200
Solve for x:
6/x=(2x)/9
x=+-3sqrt3
300
Determine the coordinate of the hole in the function
r(x)=(2x+14)/(x^2+5x-14)
r(x)=[2(x+7)]/[(x+7)(x-2)
r(-7)=2/(x-2)=2/(-7-2)=-2/9
HOLE @ (-7,-2/9)
300
Scientists measure a bacteria population and find that it is 5,000. Ten days later, they find that the population has doubled. Write a function that could describe the bacteria population x days after the scientists first measured it, assuming it grows exponentially?
P=5,000*2^(x/10)
300
Determine the equation for the function graphed below:
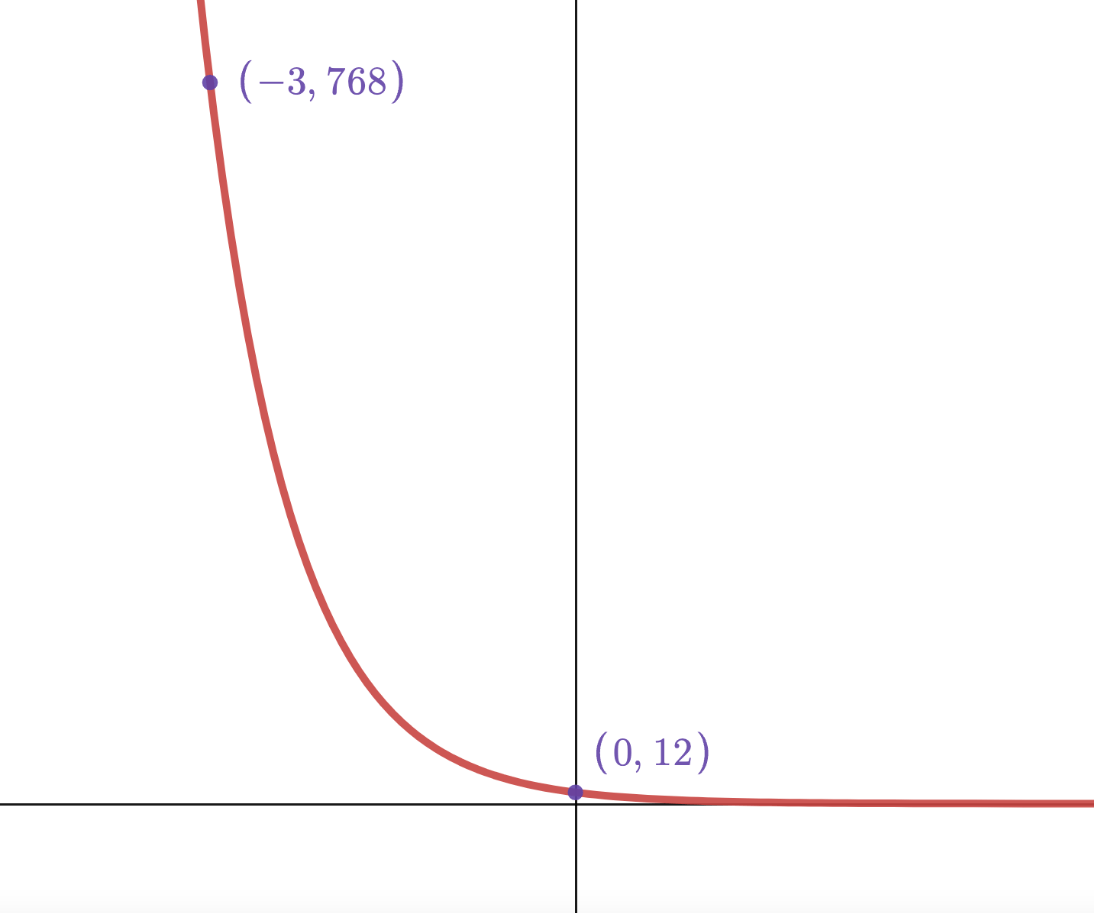
y=12*(1/4)^x
300
he population in the town of Deersburgh is presently 42,500. The town has been growing at a steady rate of 2.7% every 5 years. What will the population of the town be in 20 years?
P=42,500*1.027^4
or
P=42,500*(1.027^(1/5))^20
Approximately 47,279 people
300
Solve for x:
1/(x-2)+1/(x^2-7x+10)=6/(x-2)
x=26/5=5.2
400
Identify the equation of the slant asymptote of the function
r(x)=(3x^3)/(4x^2-8x)
y=3/4x+3/2
400
The value of a coin is increasing exponentially. Two points on a graph show the coin’s initial value and its value 4 years later. The points are (0, 8) and (4, 12). Write an expression (don’t solve it) to represent the coin’s value 7 months after purchase.
8*1.5^[(1/4)*(7/12)]
8*1.5^[(7/48)]
400
Determine the equation of the function graphed below:
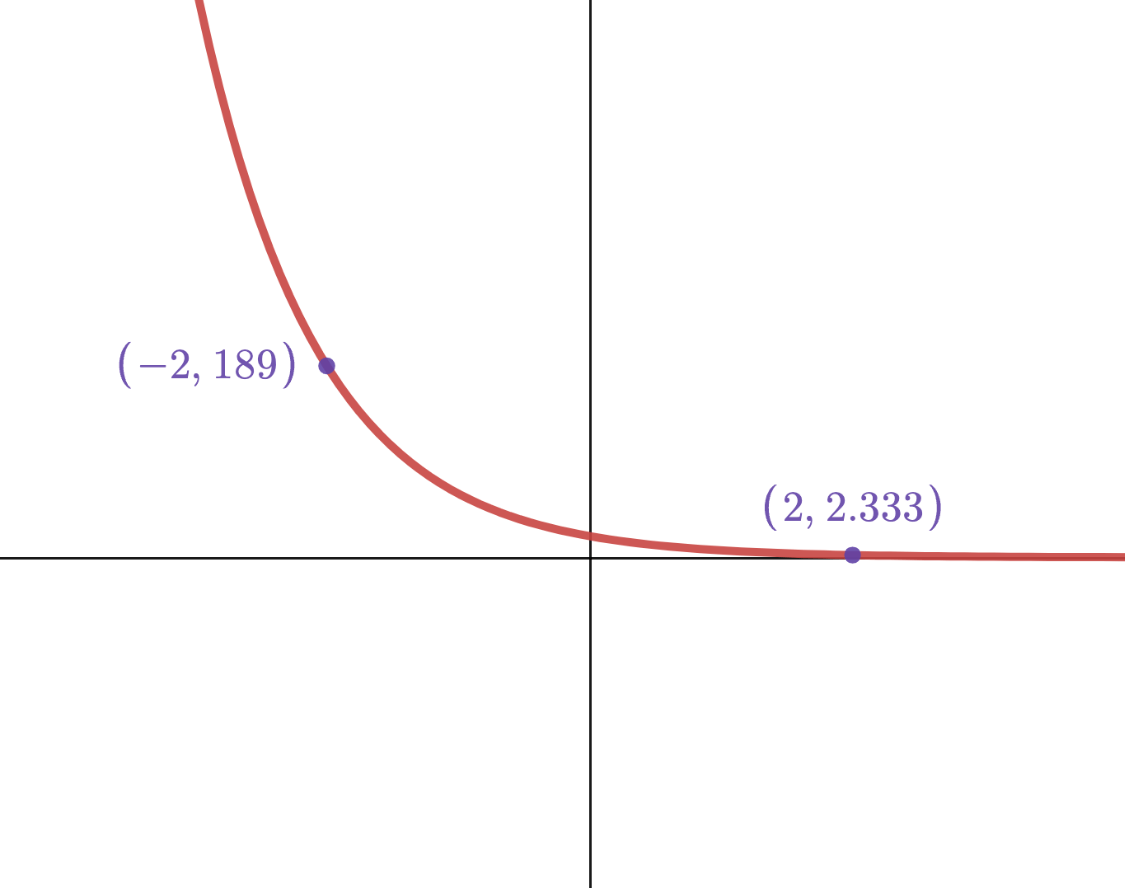
y=21*(1/3)^x
400
The value of a car was $22,000 when it was purchased. They car depreciates at a rate of 19% per year. How much will the car be worth 5 months after purchase?
C=22,000*0.81^(5/12)
$20,150.76
400
5/(x^3+5x^2)=4/(x+5)+1/x^2
x=-1/4