2 times 3^2-8
10
You decide to spend your Friday night at a local concert. The ticket cost $10. A soda at the show costs you $2 each.
Identify your variables and write an equation to represent the situation.
Let x be the number of sodas purchased.
Let y be the total cost of the evening.
y=2x+10
Write the formula for slope.
m=\frac{y_2-y_1}{x_2-x_1}
What does the variable below represent?
r
It is the correlation coefficient. It is a measure of how well the original data fits a straight line.
8x=4
x=\frac{1}{2}
(16-4)\div 6+3
5
For babysitting, Nicole charges a flat fee of $12, plus $10 per hour. Write an equation for the money Nicole earns, E, after h hours of babysitting.
What do you think the slope and the y-intercept represent?
E=10h+12
The slope is 10 because 10 is the hourly rate of change.
The y-intercept is 12 because 12 is the base amount charged for babysitting.
Suppose you graphed the three following equations.
y=x \quad \quad \quad \quad y=2x \quad \quad \quad \quad y=3x
How are the graphs alike? How are they different? Compare the slopes.
Each of the graphs is a linear line, increasing and going through the origin.
However, y=3x is the steepest line and y=x is the least steep line. The bigger the coefficient of x, the steeper the line.
Find the Least Squares Line for the data below.
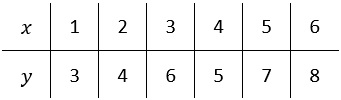
y=2.2+0.942857x
21-2x=-9x
x=-3
2+4(5-3)-3^2-15
-14
A canoe rental service charges a $20 transportation fee and $30 dollars an hour to rent a canoe. Write an equation representing the cost, y, of renting a canoe for x hours.
What is the cost of renting the canoe for 6 hours?
y=30x+20
For 6 hours, it will cost $200.
Write an equation for the points below. Use slope-intercept form.
(30,180) \quad \quad \quad \quad (50,220)
y=2x+120
Consider the data below.

The least squares line is
Y=0.555x-0.5
If x=3, then Y=1.165.
What, if anything, is wrong with this?
There is nothing wrong. The least squares line makes estimates based on data from a scatterplot. It does not give exact values unless
r=1 \quad \quad \quad or \quad \quad \quad r=-1
5x-6=3x+4
x=5
36\div 3 \times 2 -3^3
-3
A water tank already contains 55 gallons of water when Baxter begins to fill it. Water flows into the tank at a rate of 8 gallons per minute. Write a linear equation to model this situation.
Find the volume of water in the tank 25 minutes after Baxter begins filling the tank.
y=8x+55
There are 255 gallons of water after 25 minutes.
Write an equation for the line below.
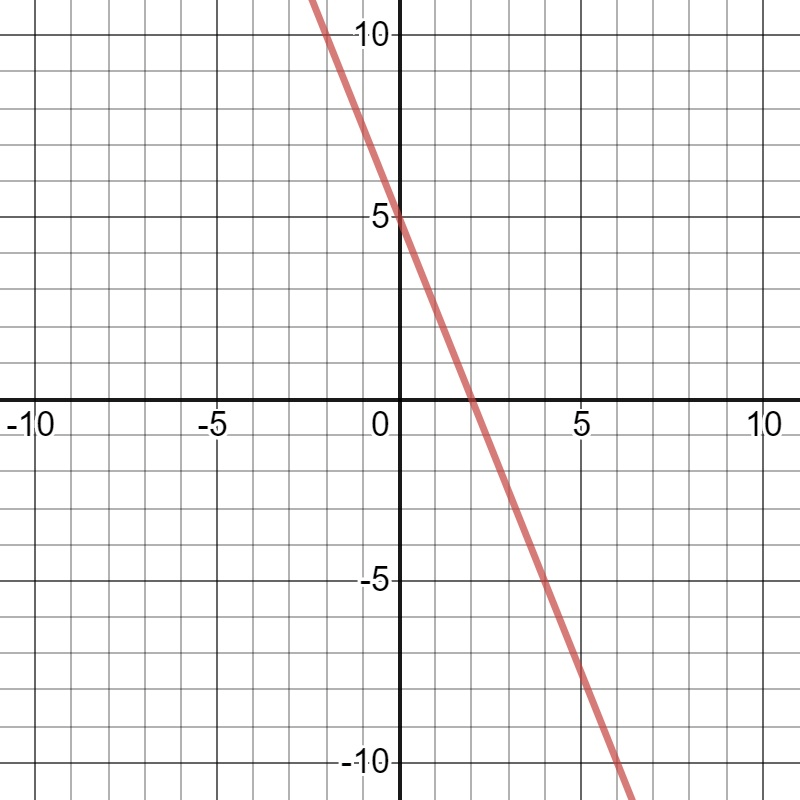
y=-\frac{5}{2}x+5
Compare the following r values. What is similar? What is different?
r=0.9583 \quad \quad and \quad \quad -0.9847
Both lines have strong linear correlation. The data for both is almost linear.
However, in the first case, it is a positive correlation and the line is increasing. In the second case, it is a negative correlation and the line is decreasing.
3(x-3)=6x-21
x=4
2[8-2(30 \div 3)-2]+20
-8
Casey has a small business making dessert baskets. She estimates that her fixed weekly costs for rent and electricity are $200. The ingredients for one dessert basket cost $2.50.
Her total costs for the week before were $562.50. How many dessert baskets did she make the week before?
y=2.50x+200
Casey made 145 dessert baskets to earn $562.50.
A caterer charges $120 to cater a party for 15 people and $200 for 25 people. Assume that the cost, y, is a linear function of the number of x people. Write an equation in slope-intercept form for this function.
y=8x
How does an outlier affect the correlation coefficient?
The correlation coefficient will be closer to zero, and imply that the data has less of a linear relationship that it actually does.
Joanne sells silk-screened T-shirts at community festivals and crafts fairs. Her cost function is
C(x)=3.50x+90
Her revenue function is
R(x)=9x
How many T-shirts must she produce and sell in order to break even?
17 shirts