Circumference
Arc Length
Sector Area
Central Angles
Inscribed Angles
SAT MATH
200
Find the circumference of the circle. Use your calculator's value of pi. Round your answer to the nearest tenth.
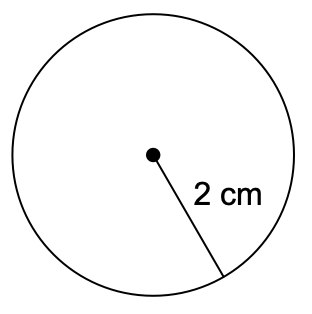
12.6 cm
200
Find the length of the bolded arc. Use your calculator's value of pi. Round your answer to the nearest tenth.
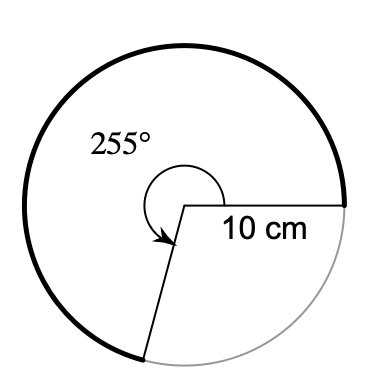
44.5 cm
200
Find the area of the bolded sector. Use your calculator's value of pi. Round your answer to the nearest tenth.
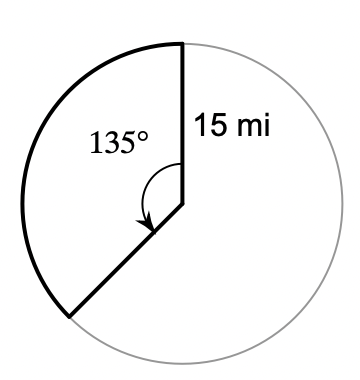
265.1 mi²
200
Find the measure of central angle BAC. Assume that lines which appear to be diameters are actual diameters.
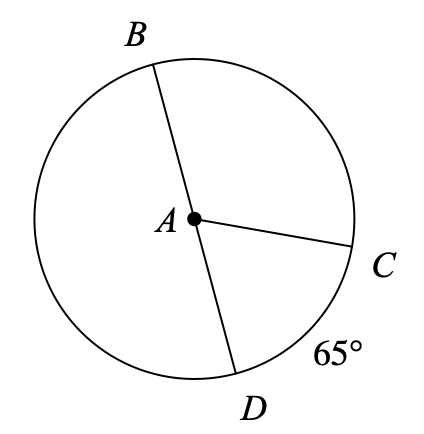
115°
200
Find the measure of the arc or angle indicated.
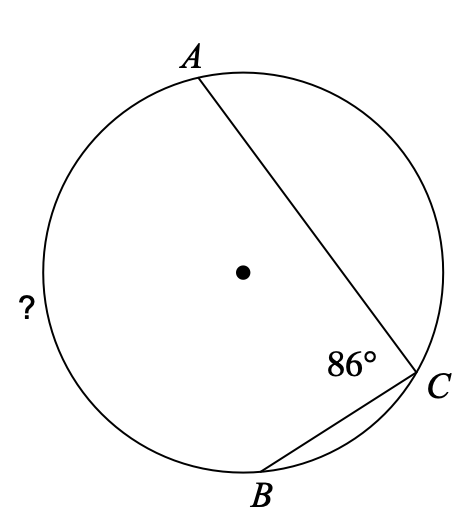
172°
400
Find the circumference of the circle. Use your calculator's value of pi. Round your answer to the nearest tenth.
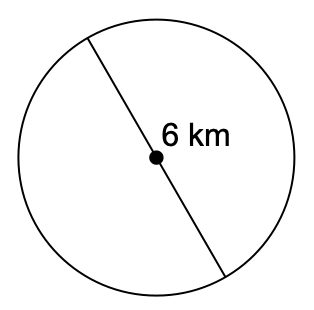
18.8 cm
400
Find the length of the bolded arc. Use your calculator's value of pi. Round your answer to the nearest tenth.
23.6 yd
400
Find the area of the bolded sector. Use your calculator's value of pi. Round your answer to the nearest tenth.
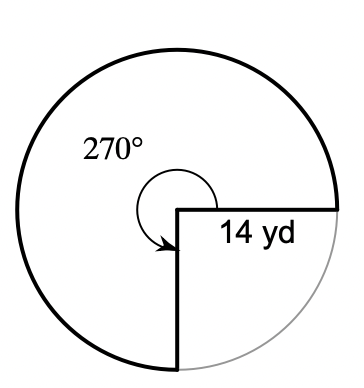
461.8 yd²
400
Solve for x. Assume that lines which appear to be diameters are actual diameters.
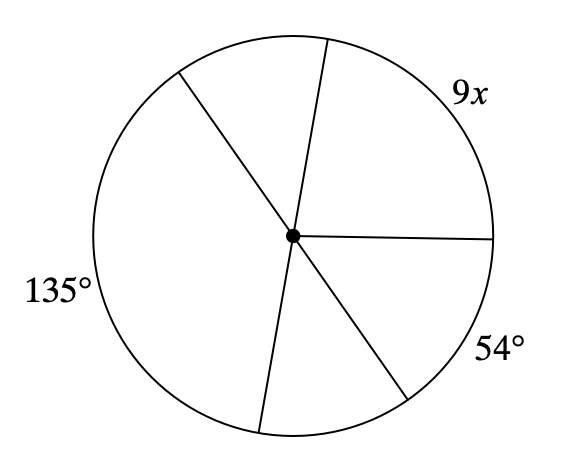
x=9
400
Solve for x.
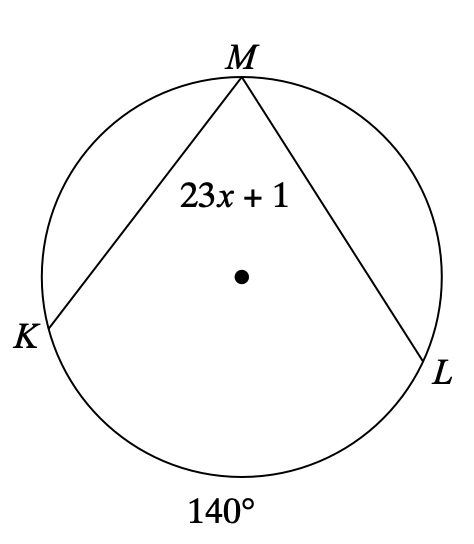
x = 3
600
Given that the area of a circle is 181.5 cm², find the circumference of the circle. Use your calculator's value of pi. Round your answer to the nearest tenth.
47.8 cm
600
If A is the area and C the circumference of a circle, which of the following is an expression for A in terms of C?
a. (C^2)/(4pi)
b. (C^2)/(4pi^2)
c. 2Csqrt(pi)
d. 2C^2sqrt(pi)
A
700
Find the measure of central angle JGH. Assume that lines which appear to be diameters are actual diameters.
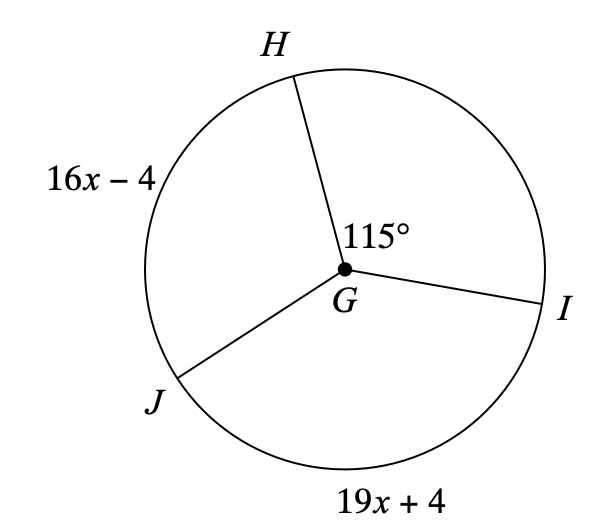
108°
700
Solve for x.
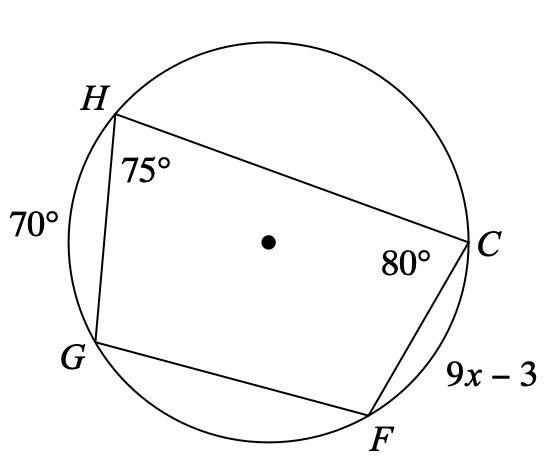
x = 7
700
Point O is the center of both circles in the figure below. If the circumference of the large circle is 36 and the radius of the small circle is half of the radius of the large circle, what is the length of the bolded arc of the smaller circle?
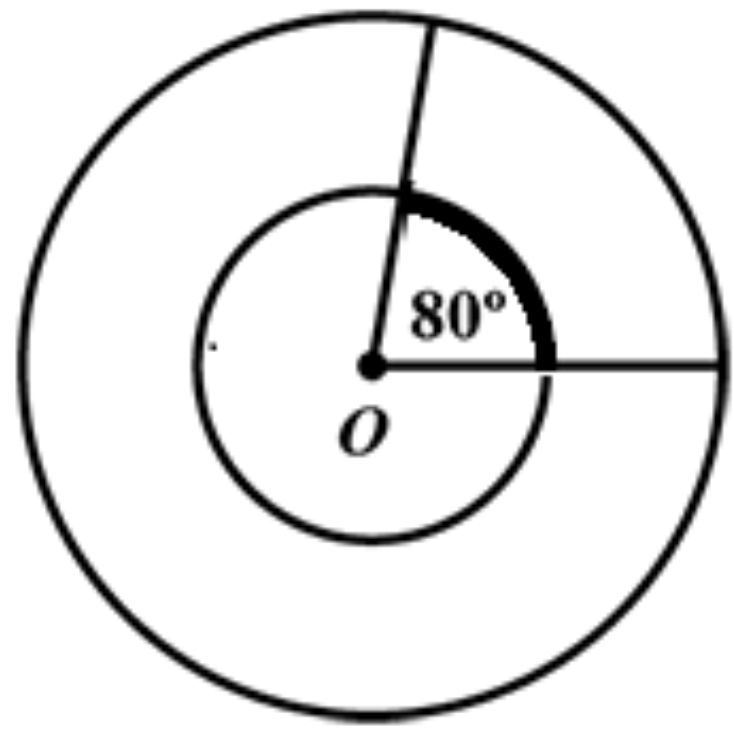
4
800
If the area of the shaded region is kpi, what is the value of k?
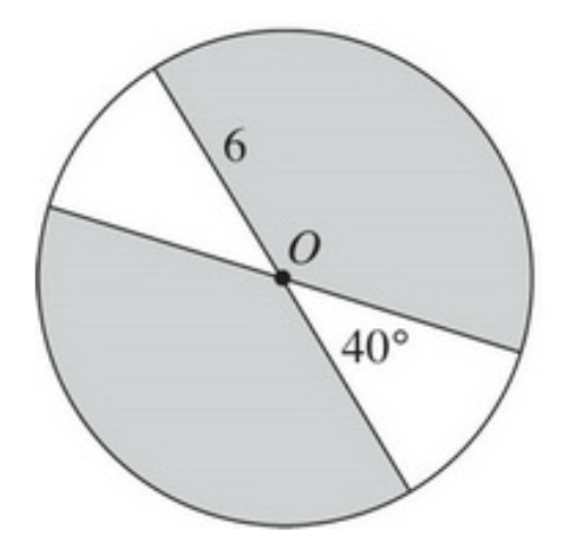
k=28