Graphing
Substitution
Elimination
Solutions or Not
Miscellaneous
100
y = 2x + 2
y = x − 1
(-3, -4)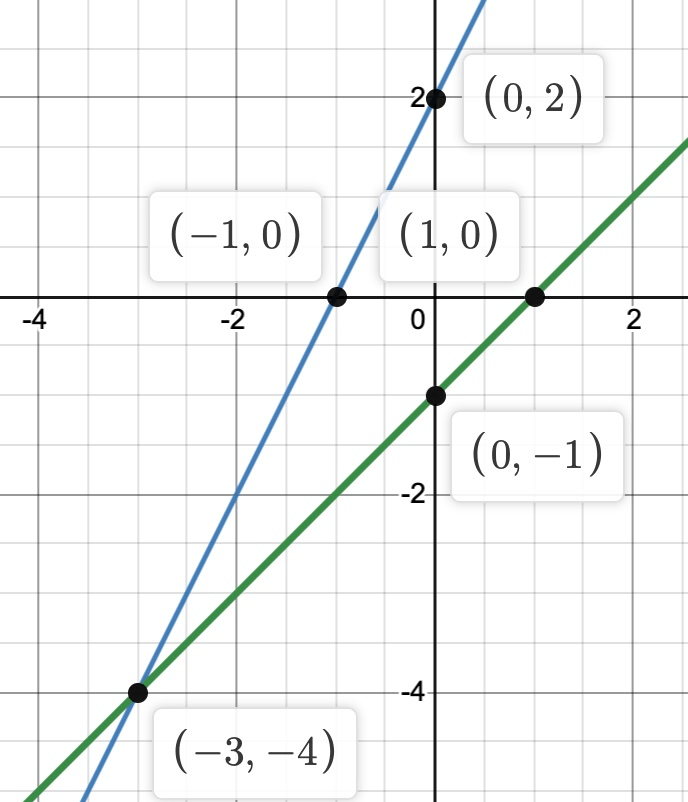
100
y = 2
3x + 2y = 10
(2, 2)
100
x + 3y = 5
2x − 3y = −8
(−1, 2)
100
Find the number of solutions and what "type" of lines
x-3y=1
-2x+6y=5
No solution - Parallel lines
100
Consists of two or more linear equations in the same variables.
System of linear equations (linear system)
200
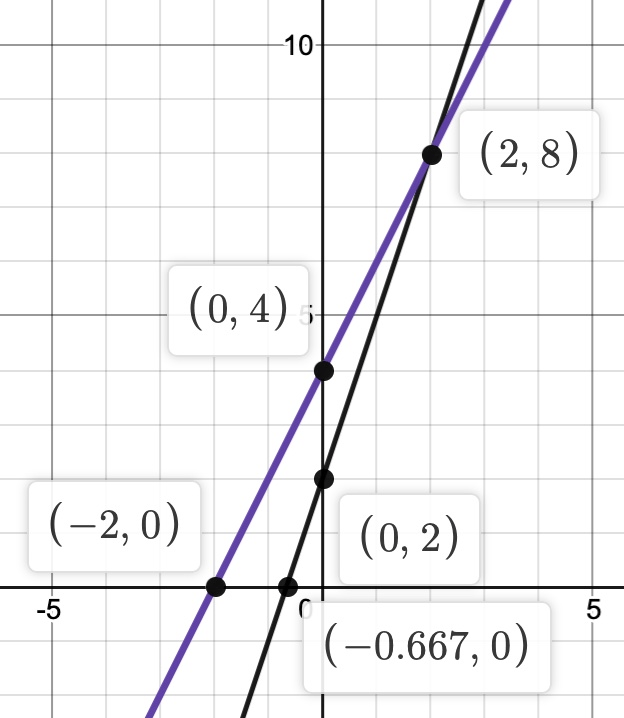
y = 2x + 4
y = 3x + 2
(2, 8)
200
x +3y= 2
−x + 2y = 3
(−1, 1)
200
−5y + 8x = −18
5y + 2x = 58
(4, 10)
200
Find the number of solutions and what "type" of lines
y-4=-2/5(x+3)
y+2=-2/5(x-12)
Infinitely Many Solutions - Coinciding Lines
200
The method of solving equations where you add equations to end up with one variable.
Elimination Method or Linear Combinations
300
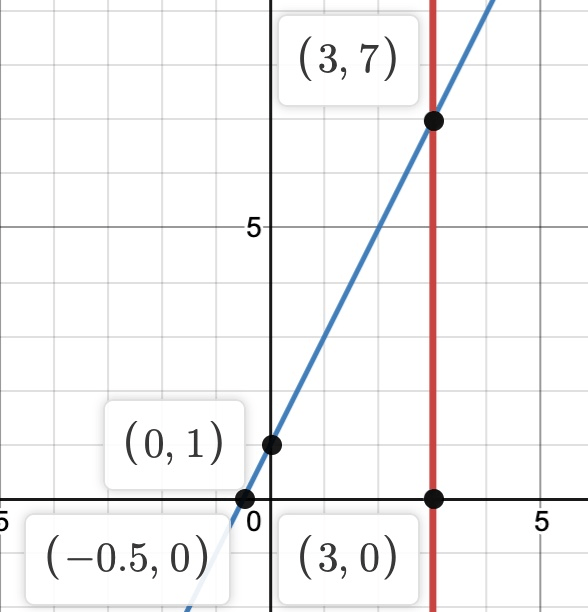
x=3
4x-2y=2
(3, 7)
300
x − 2y = −10
3x -y=0
(2, 6)
300
5x-3y=24
3x+5y=28
(6, 2)
300
Describe the system of equations as Independent, Dependent, or Inconsistent.
4x-y=9
x-3y=16
Independent
300
How can you tell if a linear system has infinitely many solutions? Include how you tell graphically and algebraically when solving.
The equations are the same, the graphed lines lie on top of one another, or solving the system provides a true statement with no variables.
400
4x + 2y = 8
2x + y = 4
Every point on 2x+y=4 is a solution.
400
2x – 3y = –2
8x+2y = 48
(5, 4)
400
x-2y=16
y+3=3x
(-2, -9)
400
Describe the system of equations as Independent, Dependent, or Inconsistent.
y=-3x+5
4y+12x=20
Dependent
400
When will a system of linear equations have no solution? Include how you tell graphically and algebraically when solving.
The lines are parallel or they have the same slope and different y-intercepts or when you solve the equations and get a false statement with no variables remaining.
500
y-1=1/2(x+2)
y-5=1/4(x-4)
(8, 6)
500
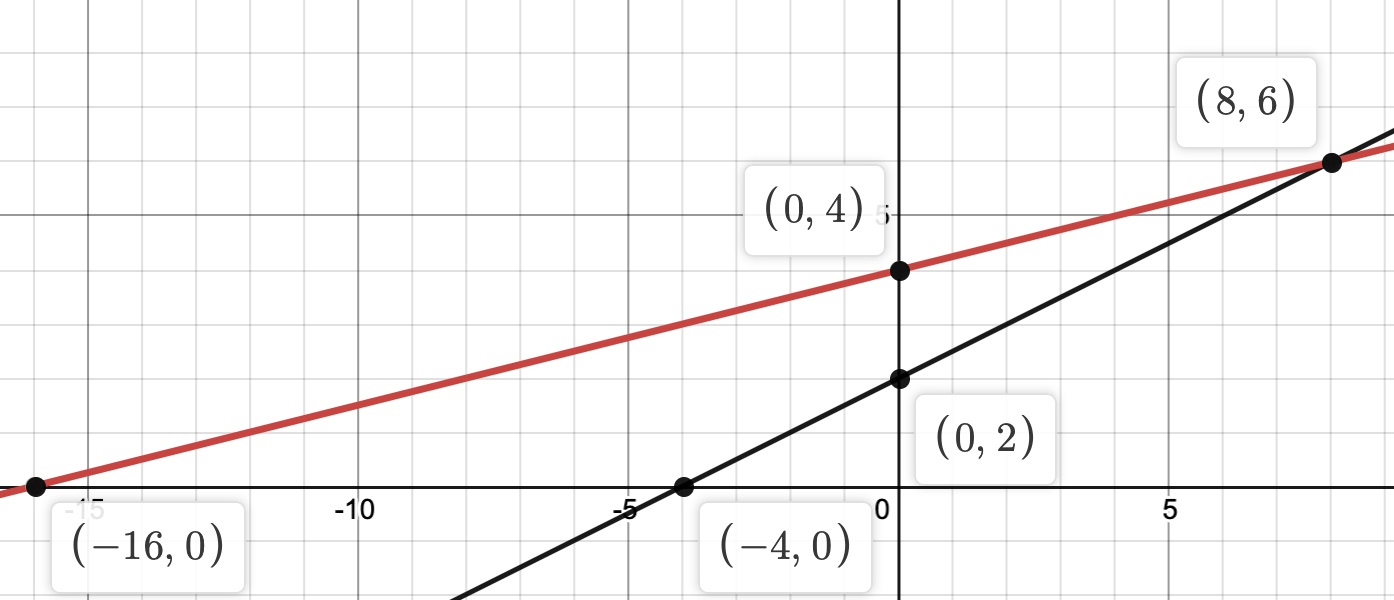
5x − 13+2y =3 y
−5x + y = 24
no solution
500
13/10x-1/5y=12
2/5 x+17y=89
(10, 5)
500
Find the number of solutions and what "type" of lines
(x+y)/4-(x-y)/3=1
(x-y)/2+(x+y)/4=-9
One Solution - Intersecting Lines
500
How does the graphing method for solving a system of linear equations work?
Graph the two lines. The solution is the point(s) of intersection.